
 (本题共16分)
(本题共16分)
已知四棱锥P-ABCD的体积为![]() ,PC
,PC![]() 底面ABCD,
底面ABCD, ![]() ABC
ABC
和![]() ACD都是边长为1的等边三角形,点E分侧棱PA所成的
ACD都是边长为1的等边三角形,点E分侧棱PA所成的
比![]() .
.
(1)当![]() 为何值时,能使平面BDE
为何值时,能使平面BDE![]() 平面ABCD?并给出证明;
平面ABCD?并给出证明;
(2)当平面BDE![]() 平面ABCD时,求P点到平面BDE的距离;
平面ABCD时,求P点到平面BDE的距离;
(3)当![]() =1时,求二面角A-BE-D的大小.
=1时,求二面角A-BE-D的大小.
解:(1)依题设,底面ABCD为菱形,设AC![]() BD=O,连结
BD=O,连结
OE,则OE⊥BD.若平面BDE⊥平面ABCD,则OE⊥平面ABCD,
∵CP⊥平面ABCD,∴OE‖CP.
∵O为AC中点,∴E为PA中点,且![]() .
.
(2)由(1)知,OE⊥平面ABCD,CP‖OE,CP‖平面BDE,
故P到平面BDE的距离即为C到平面BDE的距离,易证CO⊥
平面BDE,∴CO即为C到平面BDE的距离,
而CO=![]() AC=
AC=![]() ,∴点P到平面BDE的距离为
,∴点P到平面BDE的距离为![]() .
.
说明 亦可化为求点A到平面BDE的距离.
(3)![]() 时,即有平面BDE⊥平面ABCD,交线为BD,∵AO⊥BD,AO
时,即有平面BDE⊥平面ABCD,交线为BD,∵AO⊥BD,AO![]() 平面ABCD,∴AO⊥平面BDE,过O作OQ⊥BE于Q,连结QA,则由三垂线定理知QA⊥BE,
平面ABCD,∴AO⊥平面BDE,过O作OQ⊥BE于Q,连结QA,则由三垂线定理知QA⊥BE,
∴∠AQO就是二面角A-BE-D的平面角.
在RtΔBOE中,∵OE=![]() PC=
PC=![]() ,OB=
,OB=![]() AB=
AB=![]() ,∴BE=
,∴BE=![]() ,
,
故由![]() 得,
得,![]() .
.
在RtΔAOQ中,![]() ,即二面角A-BE-D的大小为
,即二面角A-BE-D的大小为![]()


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案科目:高中数学 来源:2011-2012学年上海市黄浦区高三上学期期终基础学业测评理科数学试卷 题型:解答题
(本题满分16分)本题共有2个小题,第1小题满分6分,第2小题满分10分.
已知两点 、
、 ,点
,点 是直角坐标平面上的动点,若将点
是直角坐标平面上的动点,若将点 的横坐标保持不变、纵坐标扩大到
的横坐标保持不变、纵坐标扩大到 倍后得到点
倍后得到点 满足
满足 .
.
(1) 求动点 所在曲线
所在曲线 的轨迹方程;
的轨迹方程;
(2)(理科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 ,又点
,又点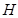 关于原点O的对称点为点
关于原点O的对称点为点 ,试问四点
,试问四点 是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
是否共圆,若共圆,求出圆心坐标和半径;若不共圆,请说明理由.
(文科)过点 作斜率为
作斜率为 的直线
的直线 交曲线
交曲线 于
于 两点,且满足
两点,且满足 (O为坐标原点),试判断点
(O为坐标原点),试判断点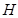 是否在曲线
是否在曲线 上,并说明理由.
上,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本题共3小题,第一小题6分,第二小题5分,第三小题5分,共16分)
在![]() 的展开式中,已知第5项的系数与第3项的系数之比是
的展开式中,已知第5项的系数与第3项的系数之比是![]() .
.
(1)求展开式中所有项的系数之和及奇数项的二项式系数之和;
(2)求展开式中的所有有理项;
(3)求展开式中系数绝对值最大的项.
注:所涉及的系数均用数字作答
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=![]()
![]() +m+1对x∈(0,
+m+1对x∈(0,![]() )的图象恒在x轴上方,则m的取值范围是 ( )
)的图象恒在x轴上方,则m的取值范围是 ( )
A.2-2![]() <m<2+2
<m<2+2![]() B.m<2
B.m<2
C. m<2+2![]() D.m≥2+2
D.m≥2+2![]()
二、填空题(本题共4小题,每题4分,共16分)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com