
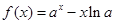 ,其中
,其中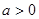 且
且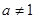 。
。 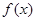 的单调性;
的单调性;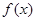 在〔
在〔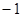 ,
,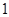 〕上的最小值和最大值。
〕上的最小值和最大值。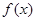 在
在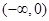 上单调递减,在
上单调递减,在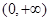 上单调递增;
上单调递增;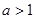 时,
时,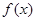 在
在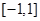 上的最小值为
上的最小值为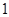 ,最大值为
,最大值为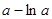 ;
;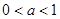 时,
时,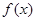 在
在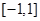 上的最小值为
上的最小值为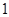 ,最大值为
,最大值为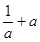
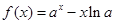 ,其中
,其中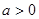 且
且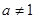 ,求解导数得到
,求解导数得到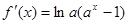 ,然后对于参数a的范围结合对数值来分类讨论得到结论。
,然后对于参数a的范围结合对数值来分类讨论得到结论。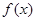 在
在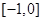 单调递减,在
单调递减,在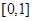 在单调递增
在单调递增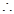 当
当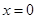 时,
时,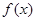 取得最小值
取得最小值
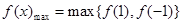 ,进而作差比较大小,得到关于a的函数,结合导数求解得到。
,进而作差比较大小,得到关于a的函数,结合导数求解得到。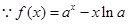 ,∴
,∴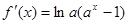 。
。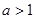 时,
时,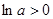 ,由
,由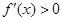 可得
可得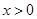 ;由
;由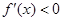 可得
可得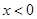
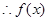 在
在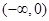 上单调递减,在
上单调递减,在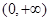 上单调递增。
上单调递增。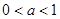 时,
时,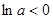 ,由
,由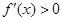 可得
可得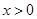 ;由
;由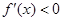 可得
可得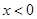
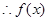 在
在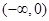 上单调递减,在
上单调递减,在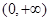 上单调递增。
上单调递增。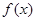 在
在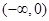 上单调递减,在
上单调递减,在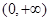 上单调递增。………4分
上单调递增。………4分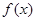 在
在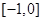 单调递减,在
单调递减,在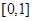 在单调递增
在单调递增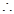 当
当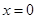 时,
时,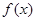 取得最小值
取得最小值
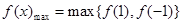 ……………………………………………………6分
……………………………………………………6分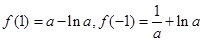 ,
,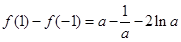
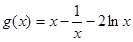 ,则
,则 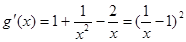 。
。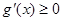 (当且仅当
(当且仅当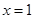 时
时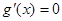 )∴
)∴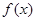 在
在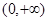 上单调递增.
上单调递增. ,
,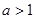 时,
时,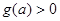 ,即
,即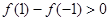 ,
,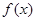 在
在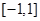 上的最大值为
上的最大值为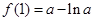 ;
;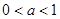 时,
时,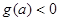 ,即
,即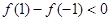
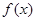 在
在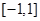 上的最大值为
上的最大值为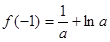 。
。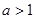 时,
时,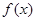 在
在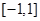 上的最小值为
上的最小值为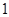 ,最大值为
,最大值为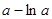 ;
;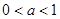 时,
时,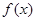 在
在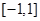 上的最小值为
上的最小值为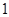 ,最大值为
,最大值为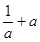 …………12分
…………12分

科目:高中数学 来源:不详 题型:解答题
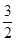 与x=-1时有极值.
与x=-1时有极值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
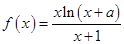
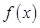 在
在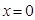 处取到极值,求
处取到极值,求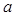 的值.
的值.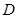 上的函数
上的函数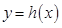 在点
在点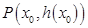 处的切线方程为
处的切线方程为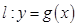 ,若
,若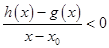 在
在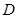 内恒成立,则称
内恒成立,则称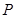 为函数的
为函数的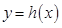 的“HOLD点”.当
的“HOLD点”.当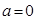 时,试问函数
时,试问函数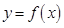 是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.
是否存在“HOLD点”,若存在,请至少求出一个“HOLD点”的横坐标;若不存在,请说明理由.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com