
(01全国卷) (12分)
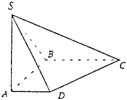
如图,在底面是直角梯形的四棱锥S―ABCD中,∠ABC = 90°,SA⊥面ABCD,SA = AB = BC = 1,![]() .
.
(Ⅰ)求四棱锥S―ABCD的体积;
(Ⅱ)求面SCD与面SBA所成的二面角的正切值.
科目:高中数学 来源: 题型:
(01全国卷文)(14分)
设f (x) 是定义在R上的偶函数,其图像关于直线x = 1对称.对任意x1,x2∈![]() 都有f (x1+x2) = f (x1) ? f (x2).
都有f (x1+x2) = f (x1) ? f (x2).
(Ⅰ)求![]() 及
及![]() ;
;
(Ⅱ)证明f (x) 是周期函数;
查看答案和解析>>
科目:高中数学 来源: 题型:
(01全国卷文) (12分)
设计一幅宣传画,要求画面面积为4840cm2,画面的宽与高的比为λ (λ<1=,画面的上、下各留8cm空白,左、右各留5cm空白.怎样确定画面的高与宽尺寸,能使宣传画所用纸张面积最小?
查看答案和解析>>
科目:高中数学 来源: 题型:
(01全国卷理)(14分)
设f (x) 是定义在R上的偶函数,其图像关于直线x = 1对称.对任意x1,x2∈[0,![]() ]都有f (x1+x2) = f (x1) ? f (x2).且f (1) = a>0.
]都有f (x1+x2) = f (x1) ? f (x2).且f (1) = a>0.
(Ⅰ)求f (![]() ) 及f (
) 及f (![]() );
);
(Ⅱ)证明f (x) 是周期函数;
(Ⅲ)记an = f (2n+![]() ),求
),求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com