练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知圆O：x2＋y2＝r2及圆外一点P(a，b)，过点P作圆O的两条切线PA，PB，切点分别为A，B，求直线AB的方程．

    答案：
    解析：

    　　分析：过圆外一点P作圆的切线PA，PB，有PA＝PB．由此，以点P为圆心，PA为半径构造辅助圆，则弦AB可以看作已知圆与辅助圆的公共弦．

    　　解：由切线长定理得PA＝PB，以P为圆心，PA为半径构造圆P，则AB可看作圆O与圆P的公共弦．如图，由切线的性质得|PA|2＝|PO|2－|OA|2＝a2＋b2－r2，

    　　所以圆P的方程为(x－a)2＋(y－b)2＝a2＋b2－r2．　①

    　　又圆O的方程为x2＋y2＝r2，　②

    　　①－②，得ax＋by－r2＝0．

    　　所以直线AB的方程为ax＋by－r2＝0．

    　　点评：本题若按常规思路，需先求得切线方程，再设法求得切点坐标，才能求出直线AB的方程．显然构造辅助圆，将问题转化为求两圆的公共弦方程更巧妙．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：辽宁省沈阳二中2011－2012学年高二上学期期中考试数学文科试题 题型：013

    已知圆O：x2＋y2＝1，点P在直线上，O为坐标原点，若圆O上存在点Q，使∠OPQ＝30°，则点P的纵坐标y0的取值范围是

    [　　]
    A．

    [－2，2]

    B．

    [0，2]

    C．

    [－1，1]

    D．

    [0，1]

    查看答案和解析>>

    科目：高中数学 来源： 题型：

           已知圆O：x2＋y2＝1，圆C：（x－4）2＋（y－4）2＝1，由两圆外一点P（a,b）引两圆切线PA、PB，切点分别为A、B，如图，满足|PA|＝|PB|；

           （Ⅰ）将两圆方程相减可得一直线方程l：x＋y－4=0，该直线叫做这两圆的“根轴”，试证点P落在根轴上；

           （Ⅱ）求切线长|PA|的最小值；

    （Ⅲ）给出定点M（0,2），设P、Q分别为直线l和圆O上动点，求|MP|＋|PQ|的最小值及此时点P的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆O：x2＋y2＝1和定点A(2,1)，由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，|PQ|＝|PA|成立，如图．

    (1)求a、b间关系；

    (2)求|PQ|的最小值；

    (3)以P为圆心作圆，使它与圆O有公共点，试在其中求出半径最小的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

     已知圆O：x2＋y2＝1和定点A(2,1)，由圆O外一点P(a，b)向圆O引切线PQ，切点为Q，|PQ|＝|PA|成立，如图．

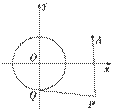
    (1)求a、b间关系；

    (2)求|PQ|的最小值；

    (3)以P为圆心作圆，使它与圆O有公共点，试在其中求出半径最小的圆的方程．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆O：x2＋y2＝1，圆C：(x－2)2＋(y－4)2＝1，由两圆外一点P(a，b)引两圆切线PA、PB，切点分别为A、B，如图，满足|PA|＝|PB|.

    (1)求实数a、b间满足的等量关系；

    (2)求切线长|PA|的最小值；

    (3)是否存在以P为圆心的圆，使它与圆O相内切并且与圆C相外切？若存在，求出圆P的方程；若不存在，说明理由.

    查看答案和解析>>

    同步练习册答案