
已知函数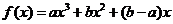 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为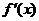 .
.
(1)当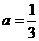 时,若不等式
时,若不等式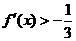 对任意
对任意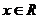 恒成立,求
恒成立,求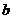 的取值范围;
的取值范围;
(2)若函数 为奇函数,且在
为奇函数,且在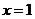 处的切线垂直于直线
处的切线垂直于直线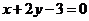 ,关于x的方程
,关于x的方程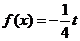 在
在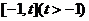 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
已知函数 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为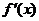 .
.
(1)当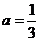 时,若不等式
时,若不等式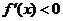 对任意
对任意
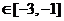 恒成立,求b的取值范围;
恒成立,求b的取值范围;
(2)若函数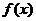 为奇函数,且在
为奇函数,且在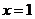 处的切线垂直于直线
处的切线垂直于直线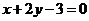 ,关于x的方程
,关于x的方程 在
在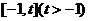 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
解:(1)当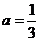 时,
时,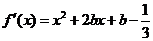 ,………1分
,………1分
依题意 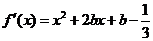
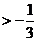 即
即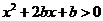 恒成立
恒成立
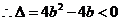 ,解得
,解得 
所以b的取值范围是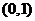 …………………………………4分
…………………………………4分
(2)因为 为奇函数,所以
为奇函数,所以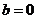 ,所以
,所以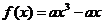 ,
,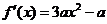 .又
.又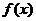 在
在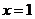 处的切线垂直于直线
处的切线垂直于直线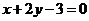 ,所以
,所以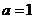 ,即
,即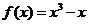 .…………………………………………………6分
.…………………………………………………6分
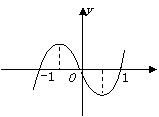
|
 在
在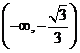 ,
,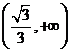 上是单调递增函数,在
上是单调递增函数,在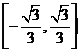 上是单调递减函数,由
上是单调递减函数,由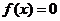 解得
解得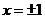 ,
, ,……………………………7分
,……………………………7分
法一:如图所示,作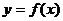 与
与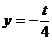 的图像,若只有一个交点,则
的图像,若只有一个交点,则
|
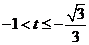 时,
时,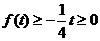 ,
,
|


|
|
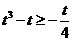 ,解得
,解得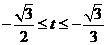 ;
;

|
|
|
|

|
|
|
|
|
|
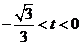 时,
时,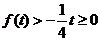 ,
,
解得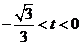 ;
;
|
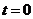 时,不成立;
时,不成立;
|


|

|
|
|
|
|
 时,
时,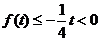 ,
,
|
|
|


|

|
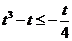 ,解得
,解得 ;
;
|
|
 ⑤当
⑤当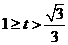 时,
时,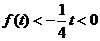 ,
,




|
|
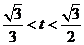 ;
;
|
|
 ⑥当
⑥当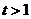 时,
时,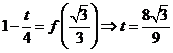 .
.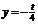
………………………………………………………………………13分
综上t的取值范围是 或
或 或
或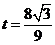 .…………………14分
.…………………14分
法二:由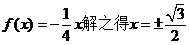 .
. 
作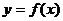 与
与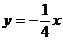 的图知交点横坐标为
的图知交点横坐标为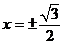 ,
,
当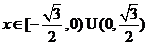
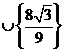 时,过
时,过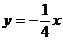 图象上任意一点向左作平行于
图象上任意一点向左作平行于 轴的直线与
轴的直线与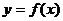 都只有唯一交点,当
都只有唯一交点,当 取其它任何值时都有两个或没有交点。
取其它任何值时都有两个或没有交点。
所以当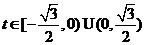
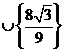 时,方程
时,方程 在
在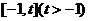 上有且只有一个实数根.
上有且只有一个实数根.


 小题狂做系列答案
小题狂做系列答案科目:高中数学 来源:乌鲁木齐2008年高三年级第三次诊断性测验文理科数学试卷及详解答案 题型:013
已知函数![]() ,a,b是实数,则a+b≥0是f(a)+f(b)≥0成立的
,a,b是实数,则a+b≥0是f(a)+f(b)≥0成立的
A.充分非必要条件
B.必要非充分条件
C.充要条件
D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省韶关市高三第一次调研考试文科数学 题型:解答题
.(本题满分14分) 已知函数 (a,b是不同时为零的常数),其导函数为
(a,b是不同时为零的常数),其导函数为 .
.
(1)当 时,若不等式
时,若不等式 对任意
对任意 恒成立,求
恒成立,求 的取值范围;
的取值范围;
(2)若函数 为奇函数,且在
为奇函数,且在 处的切线垂直于直线
处的切线垂直于直线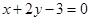 ,关于x的方程
,关于x的方程 在
在 上有且只有一个实数根,求实数t的取值范围.
上有且只有一个实数根,求实数t的取值范围.
查看答案和解析>>
科目:高中数学 来源:江西省09-10学年度高二下学期期末联考考试数学试题(文科) 题型:选择题
已知函数 若a,b,c均不相等,且
若a,b,c均不相等,且 ,则
,则 的取值范围是
的取值范围是
(A)(1,10) (B)(5,6) (C)(10,12) (D)(20,24)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com