
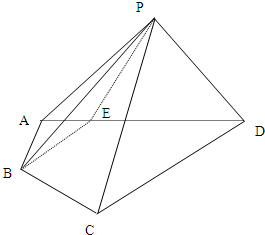
 (2006•朝阳区二模)四棱锥P-ABCD中,侧面APD⊥底面ABCD,∠APD=∠BAD=90°,∠ADC=60°,E为AD上一点,AE=2,AP=6,AD=CD=8,AB=2
(2006•朝阳区二模)四棱锥P-ABCD中,侧面APD⊥底面ABCD,∠APD=∠BAD=90°,∠ADC=60°,E为AD上一点,AE=2,AP=6,AD=CD=8,AB=2| 3 |
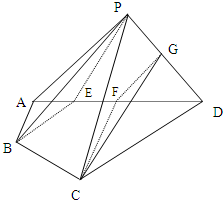 (Ⅰ)证明:
(Ⅰ)证明:| 3 |
| 3 |
| FC |
| FG |
4
| ||
| 3 |
4
| ||
| 3 |
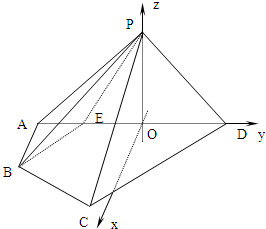
| 7 |
| 2 |
3
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| PD |
| 7 |
| 2 |
3
| ||
| 2 |
| PC |
| 3 |
| 1 |
| 2 |
3
| ||
| 2 |
| m |
|
|
| 3 |
| m |
| 3 |
| 7 |
| n |
| m |
| n |
| 3 |
| 7 |
| 3 |
| m |
| n |
| 3+9+7 |
| 19 |
| ||
|
| ||
| 19 |
| ||
| 19 |
| ||
| 19 |


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com