
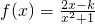 的定义域为[α,β].
的定义域为[α,β].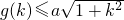 成立,
成立,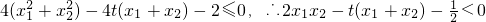

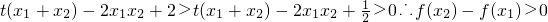
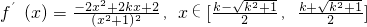
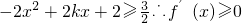
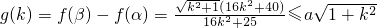 恒成立.
恒成立.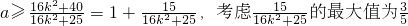 ,∴
,∴ …(13分)
…(13分) ,从而可判断
,从而可判断 的符号,即可判断函数f(x)在定义域内的单调性;
的符号,即可判断函数f(x)在定义域内的单调性;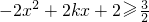 ,从而可判断f′(x)的符号,可以判断函数f(x)在定义域内的单调性;
,从而可判断f′(x)的符号,可以判断函数f(x)在定义域内的单调性;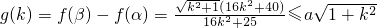 ,分离出a,即整理成k是a的函数,利用基本不等式可求得a的取值范围.
,分离出a,即整理成k是a的函数,利用基本不等式可求得a的取值范围. ”符号的确定及证法二中“
”符号的确定及证法二中“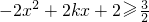 ”的分析,考查学生的综合分析与转化能力,属于难题.
”的分析,考查学生的综合分析与转化能力,属于难题. 

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
| b |
| a |
| c |
| a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com