
【题目】我国西部某省![]() 级风景区内住着一个少数民族村,该村投资了
级风景区内住着一个少数民族村,该村投资了![]() 万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按
万元修复和加强民俗文化基础设施,据调查,修复好村民俗文化基础设施后,任何一个月内(每月按![]() 天计算)每天的旅游人数
天计算)每天的旅游人数![]() 与第
与第![]() 天近似地满足
天近似地满足![]() (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费![]() 近似地满足
近似地满足![]() (元).
(元).
(1)求该村的第x天的旅游收入![]() ,并求最低日收入为多少?(单位:千元,
,并求最低日收入为多少?(单位:千元,![]() ,
,![]() );
);
(2)若以最低日收入的![]() 作为每一天的纯收入计量依据,并以纯收入的
作为每一天的纯收入计量依据,并以纯收入的![]() 税率收回投资成本,试问该村在两年内能否收回全部投资成本?
税率收回投资成本,试问该村在两年内能否收回全部投资成本?
【答案】(1) ,日最低收入为
,日最低收入为![]() 千元;(2)能.
千元;(2)能.
【解析】
(1)根据旅游收入p(x)等于每天的旅游人数f(x)与游客人均消费g(x)的乘积,然后去绝对值,从而得到所求;
(2)分别研究每一段函数的最值,第一段利用基本不等式求最小值,第二段利用函数的单调性研究最小值,再比较从而得到日最低收入,最后根据题意可判断该村在两年内能否收回全部投资成本.
(1)依据题意,有![]() (
(![]() ,
,![]() )
)
即 ,
,
![]() 当
当![]() 时,
时,![]()
(当且仅当![]() 时,等号成立) . 因此,
时,等号成立) . 因此,![]() (千元) .
(千元) .
![]() 当
当![]() 时,
时,![]() .
.
易知函数![]()
在![]() 上单调递减,于是,
上单调递减,于是,![]() (千元) .
(千元) .
又![]() ,所以,日最低收入为
,所以,日最低收入为![]() 千元.
千元.
(2)该村两年可收回的投资资金为![]() (千元)=
(千元)= ![]() (万元).
(万元).
因为![]() 万元
万元![]()
![]() 万元,所以,该村两年内能收回全部投资资金.
万元,所以,该村两年内能收回全部投资资金.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案科目:高中数学 来源: 题型:
【题目】过双曲线![]() 的左焦点
的左焦点![]() 作圆
作圆![]() 的切线交双曲线的右支于点
的切线交双曲线的右支于点![]() ,且切点为
,且切点为![]() ,已知
,已知![]() 为坐标原点,
为坐标原点,![]() 为线段
为线段![]() 的中点(
的中点(![]() 点在切点
点在切点![]() 的右侧),若
的右侧),若![]() 的周长为
的周长为![]() ,则双曲线的渐近线的方程为( )
,则双曲线的渐近线的方程为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,椭圆
为坐标原点,椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() .过焦点且垂直于
.过焦点且垂直于![]() 轴的直线与椭圆
轴的直线与椭圆![]() 相交所得的弦长为3,直线
相交所得的弦长为3,直线![]() 与椭圆
与椭圆![]() 相切.
相切.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)是否存在直线![]() :
:![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,使得
两点,使得![]() ?若存在,求
?若存在,求![]() 的取值范围;若不存在,请说明理由!
的取值范围;若不存在,请说明理由!
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数且
为参数且 ![]() )曲线
)曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数,且
为参数,且![]() ),以
),以![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为:
的极坐标方程为:![]() ,曲线
,曲线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求![]() 与
与![]() 的交点到极点的距离;
的交点到极点的距离;
(2)设![]() 与
与![]() 交于
交于![]() 点,
点,![]() 与
与![]() 交于
交于![]() 点,当
点,当![]() 在
在![]() 上变化时,求
上变化时,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
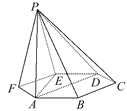
【题目】如图,已知六棱锥P-ABCDEF的底面是正六边形,PA⊥平面ABC,PA=2AB,则下列结论中:①PB⊥AE;②平面ABC⊥平面PBC;③直线BC∥平面PAE;④∠PDA=45°.
其中正确的有____________(把所有正确的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来大气污染防治工作得到各级部门的重视,某企业在现有设备下每日生产总成本![]() (单位:万元)与日产量
(单位:万元)与日产量![]() (单位:吨)之间的函数关系式为
(单位:吨)之间的函数关系式为![]() ,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为
,现为了配合环境卫生综合整治,该企业引进了除尘设备,每吨产品除尘费用为![]() 万元,除尘后当日产量
万元,除尘后当日产量![]() 时,总成本
时,总成本![]() .
.
(1)求![]() 的值;
的值;
(2)若每吨产品出厂价为48万元,试求除尘后日产量为多少时,每吨产品的利润最大,最大利润为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,半径为2的![]() 切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交
切直线MN于点P,射线PK从PN出发绕点P逆时针方向旋转到PM,旋转过程中,PK交![]() 于点Q,设
于点Q,设![]() 为x,弓形PmQ的面积为
为x,弓形PmQ的面积为![]() ,那么
,那么![]() 的图象大致是
的图象大致是![]()
![]()

A.  B.
B. 
C.  D.
D. 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com