
【题目】设数列![]() ,
,![]() ,
,![]() 的前
的前![]() 项和分别为
项和分别为![]() ,
,![]() ,
,![]() ,且对任意的
,且对任意的![]() 都有
都有![]() ,已知
,已知![]() ,数列
,数列![]() 和
和![]() 是公差不为0的等差数列,且各项均为非负整数.
是公差不为0的等差数列,且各项均为非负整数.
(1)求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() 的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列
的前4项删去1项后按原来顺序成等比数列,求所有满足条件的数列![]() ;
;
(3)若![]() ,且
,且![]() ,
,![]() ,求数列
,求数列![]() ,
,![]() 的通项公式.
的通项公式.
【答案】(1)见解析(2)![]() 或
或![]() 或
或![]() .(3)
.(3)![]() ,
,![]() ,
,![]() .
.
【解析】
(1)根据![]() 得
得![]() 作差即可得证;
作差即可得证;
(2)分类讨论删除的项,分析等比数列的通项公式;
(3)求出![]() ,根据
,根据![]() ,所以
,所以![]() ,转化为不等式恒成立求参数,即可得解.
,转化为不等式恒成立求参数,即可得解.
解:(1)因为![]() ,①
,①
所以![]() ,②
,②
②-①得![]() ,
,
即![]() ,③
,③
所以![]() .④
.④
④-③得![]() ,即
,即![]()
因为![]() ,所以数列
,所以数列![]() 是等差数列.
是等差数列.
(2)在![]() 中,令
中,令![]() 得
得![]() ,
,
设数列![]() 的公差为
的公差为![]() ,则
,则![]() ,
,
因为数列![]() 的前4项
的前4项![]() ,
,![]() ,
,![]() ,
,![]() 删去1项后成等比数列,所以有
删去1项后成等比数列,所以有
①若删去![]() 或
或![]() ,剩下的三项连续,若成等比数列,则
,剩下的三项连续,若成等比数列,则![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() ;
;
②若删去![]() ,即
,即![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,解得
,解得![]() 或
或![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() 或
或![]() ;
;
③若删去![]() ,即
,即![]() ,
,![]() ,
,![]() 成等比数列,则
成等比数列,则![]() ,解得
,解得![]() 或
或![]() ,则数列
,则数列![]() 的通项公式为
的通项公式为![]() 或
或![]() .
.
综上所述,满足条件的数列![]() 有
有![]() 或
或![]() 或
或![]() .
.
(3)![]() ,则
,则![]() ,
,![]() .
.
因为对任意的![]() 都有
都有![]() ,所以对任意的
,所以对任意的![]() 都有
都有![]() .
.
设数列![]() ,
,![]() 的公差分别为
的公差分别为![]() ,
,![]() ,则
,则
![]() ,
,![]() ,
,
所以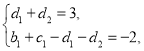 即
即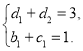 ①
①
因为对任意的![]() 都有
都有![]() ,
,
所以![]() ,
,
整理得![]() ,
,![]() ,
,
所以![]() ,且由
,且由![]() 可得
可得![]() ,②
,②
因为数列![]() ,
,![]() 的各项均为非负整数,
的各项均为非负整数,
所以由②得![]() ,
,![]() .③
.③
由①③得![]() 且
且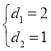 ,
,
故![]() ,
,![]() ,
,![]() .
.


 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案科目:高中数学 来源: 题型:
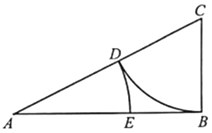
【题目】古希腊雅典学派算学家欧道克萨斯提出了“黄金分割”的理论,利用尺规作图可画出己知线段的黄金分割点,具体方法如下:(l)取线段AB=2,过点B作AB的垂线,并用圆规在垂线上截取BC=![]() AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:
AB,连接AC;(2)以C为圆心,BC为半径画弧,交AC于点D;(3)以A为圆心,以AD为半径画弧,交AB于点E.则点E即为线段AB的黄金分割点.若在线段AB上随机取一点F,则使得BE≤AF≤AE的概率约为( )(参考数据:![]() 2.236)
2.236)
A. 0.236B. 0.382C. 0.472D. 0.618
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P一ABCD中,AB=AD=2BC=2,BC∥AD,AB⊥AD,△PBD为正三角形.且PA=2![]() .
.
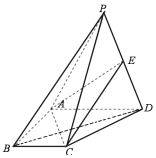
(1)证明:平面PAB⊥平面PBC;
(2)若点P到底面ABCD的距离为2,E是线段PD上一点,且PB∥平面ACE,求四面体A-CDE的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】随着医院对看病挂号的改革,网上预约成为了当前最热门的就诊方式,这解决了看病期间病人插队以及医生先治疗熟悉病人等诸多问题;某医院研究人员对其所在地区年龄在10~60岁间的![]() 位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.
位市民对网上预约挂号的了解情况作出调查,并将被调查的人员的年龄情况绘制成频率分布直方图,如下图所示.

(Ⅰ)若被调查的人员年龄在20~30岁间的市民有300人,求被调查人员的年龄在40岁以上(含40岁)的市民人数;
(Ⅱ)若按分层抽样的方法从年龄在![]() 以内及
以内及![]() 以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在
以内的市民中随机抽取5人,再从这5人中随机抽取2人进行调研,求抽取的2人中,至多1人年龄在![]() 内的概率.
内的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)求函数![]() 的单调区间;
的单调区间;
(2)若![]() 在
在![]() 上恒成立,求实数
上恒成立,求实数![]() 的取值范围;
的取值范围;
(3)在(2)的条件下(提示:可以用第(2)问的结论),任意的![]() ,证明:
,证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代典籍《周易》用“卦”描述万物的变化,每一卦由六爻组成.其中有一种起卦方法称为“金钱起卦法”,其做法为:取三枚相同的钱币合于双手中,上下摇动数下使钱币翻滚摩擦,再随意抛撒钱币到桌面或平盘等硬物上,如此重复六次,得到六爻.若三枚钱币全部正面向上或全部反面向上,就称为变爻.若每一枚钱币正面向上的概率为![]() ,则一卦中恰有两个变爻的概率为( )
,则一卦中恰有两个变爻的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
为参数),以坐标原点O为极点,x轴正半轴为极轴建立极坐标系,曲线C2:ρ2﹣4ρcosθ+3=0.
(1)求曲线C1的一般方程和曲线C2的直角坐标方程;
(2)若点P在曲线C1上,点Q曲线C2上,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“共享单车”的出现,为我们提供了一种新型的交通方式。某机构为了调查人们对此种交通方式的满意度,从交通拥堵不严重的A城市和交通拥堵严重的B城市分别随机调查了20个用户,得到了一个用户满意度评分的样本,并绘制出茎叶图如图:

(1)根据茎叶图,比较两城市满意度评分的平均值的大小及方差的大小(不要求计算出具体值,给出结论即可);
(2)若得分不低于80分,则认为该用户对此种交通方式“认可”,否则认为该用户对此种交通方式“不认可”,请根据此样本完成此2×2列联表,并据此样本分析是否有95%的把握认为城市拥堵与认可共享单车有关;
A | B | 合计 | |
认可 | |||
不认可 | |||
合计 |
(3)在A,B城市对此种交通方式“认可”的用户中按照分层抽样的方法抽取6人,若在此6人中推荐2人参加“单车维护”志愿活动,求A城市中至少有1人的概率。
参考数据如下:(下面临界值表供参考)
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式 ,其中
,其中![]() )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com