
【题目】已知函数![]()
(1)讨论函数f(x)的极值点的个数;
(2)若f(x)有两个极值点x1、x2,证明:f(x1)+f(x2)>3-4ln2.
【答案】(Ⅰ)(ⅰ)![]() 时,
时,![]() 仅有一个极值点;(ⅱ) 当
仅有一个极值点;(ⅱ) 当![]() 时,
时,![]() 无极值点;
无极值点;
(ⅲ)当![]() 时,
时,![]() 有两个极值点.(Ⅱ)详见解析
有两个极值点.(Ⅱ)详见解析
【解析】试题(Ⅰ)先求导数,再确定导函数零点情况,这需分类讨论:一次与二次的讨论,二次中有根与无根的讨论,两根情况分相等、一正一负、两不等正根,最后根据对应情况确定导函数符号变化规律,确定对应极值点个数;(Ⅱ)由(Ⅰ)先确定![]() 有两个极值点时,
有两个极值点时,![]() 的取值范围,以及
的取值范围,以及![]() 满足条件,再化简
满足条件,再化简![]() 为
为![]() 的函数,最后根据导数确定对应函数单调性,根据单调性证明不等式.
的函数,最后根据导数确定对应函数单调性,根据单调性证明不等式.
试题解析:解:(Ⅰ)由![]() 得,
得,
![]()
(ⅰ)![]() 时,
时,![]() ,
,![]()
所以![]() 取得极小值,
取得极小值,![]() 是
是![]() 的一个极小值点.
的一个极小值点.
(ⅱ)![]() 时,
时,![]() ,令
,令![]() ,得
,得![]()
显然,![]() ,所以
,所以![]() ,
,
![]() 在
在![]() 取得极小值,
取得极小值,![]() 有一个极小值点.
有一个极小值点.
(ⅲ)![]() 时,
时,![]() 时,即
时,即![]() 在
在![]() 是减函数,
是减函数,![]() 无极值点.
无极值点.
当![]() 时,
时,![]() ,令
,令![]() ,得
,得![]()
当![]() 和
和![]() 时
时![]() ,
,![]() 时,
时,![]() ,所以
,所以![]() 在
在![]() 取得极小值,在
取得极小值,在![]() 取得极大值,所以
取得极大值,所以![]() 有两个极值点.
有两个极值点.
综上可知:(ⅰ)![]() 时,
时,![]() 仅有一个极值点;
仅有一个极值点;
(ⅱ) 当![]() 时,
时,![]() 无极值点;
无极值点;
(ⅲ)当![]() 时,
时,![]() 有两个极值点.
有两个极值点.
(Ⅱ)由(Ⅰ)知,当且仅当![]() 时,
时,![]() 有极小值点
有极小值点![]() 和极大值点
和极大值点![]() ,且
,且
![]() 是方程
是方程![]() 的两根,所以
的两根,所以![]() ,
,
![]()
![]()
![]() ,
,
设![]() ,
,![]() ,
,
所以![]() 时,
时,![]() 是减函数,
是减函数,![]() ,则
,则![]()
所以![]() 得证.
得证.


 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)求![]() 的单调区间;
的单调区间;
(Ⅱ)求![]() 在区间
在区间![]() 上的最小值.
上的最小值.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】(Ⅰ)![]() .
.
令![]() ,得
,得![]() .
.

![]() 与
与![]() 的情况如上:
的情况如上:
所以,![]() 的单调递减区间是
的单调递减区间是![]() ,单调递增区间是
,单调递增区间是![]() .
.
(Ⅱ)当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,
时,
由(Ⅰ)知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
当![]() ,即
,即![]() 时,函数
时,函数![]() 在
在![]() 上单调递减,
上单调递减,
所以![]() 在区间
在区间![]() 上的最小值为
上的最小值为![]() .
.
综上,当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() ;
;
当![]() 时,
时,![]() 的最小值为
的最小值为![]() .
.
【题型】解答题
【结束】
19
【题目】已知抛物线![]() 的顶点在原点,焦点在坐标轴上,点
的顶点在原点,焦点在坐标轴上,点![]() 为抛物线
为抛物线![]() 上一点.
上一点.
(1)求![]() 的方程;
的方程;
(2)若点![]() 在
在![]() 上,过
上,过![]() 作
作![]() 的两弦
的两弦![]() 与
与![]() ,若
,若![]() ,求证: 直线
,求证: 直线![]() 过定点.
过定点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 为奇函数,
为奇函数, ![]() 为偶函数,且
为偶函数,且![]() .
.
(1)求![]() 及
及![]() 的解析式及定义域;
的解析式及定义域;
(2)若关于![]() 的不等式
的不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
(3)如果函数![]() ,若函数
,若函数![]() 有两个零点,求实数
有两个零点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市100户居民的月平均用电量(单位:度)以[160,180)[180,200)[200,220)[220,240)[240,260)[260,280)[280,300)分组的频率分布直方图如图所示:
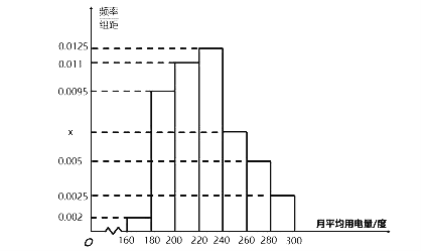
(1)求直方图中![]() 的值;
的值;
(2)用分层抽样的方法从[260,280)和[280,300)这两组用户中确定6人做随访,再从这6人中随机抽取2人做问卷调查,则这2人来自不同组的概率是多少?
(3)求月平均用电量的众数和中位数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】按文献记载,《百家姓》成文于北宋初年,表1记录了《百家姓》开头的24大姓氏:
表1:
赵 | 钱 | 孙 | 李 | 周 | 吴 | 郑 | 王 | 冯 | 陈 | 褚 | 卫 |
蒋 | 沈 | 韩 | 杨 | 朱 | 秦 | 尤 | 许 | 何 | 吕 | 施 | 张 |
表2记录了2018年中国人口最多的前10大姓氏:
表2:
1:李 | 2:王 | 3:张 | 4:刘 | 5:陈 |
6:杨 | 7:赵 | 8:黄 | 9:周 | 10:吴 |
从《百家姓》开头的24大姓氏中随机选取1个姓氏,则这个姓氏是2018年中国人口最多的前10大姓氏的概率为_____________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系,曲线
轴的正半轴为极轴建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ,曲线
,曲线![]() C的极坐标方程为
C的极坐标方程为![]() .
.
(1)求曲线![]() 的普通方程和
的普通方程和![]() 的直角坐标方程;
的直角坐标方程;
(2)设![]() 分别交
分别交![]() 于点
于点![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的两个焦点分别为
的两个焦点分别为![]() ,离心率为
,离心率为![]() ,过
,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,且
两点,且![]() 的周长为
的周长为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 分别交于
分别交于![]() 两点,且
两点,且![]() ,试问点
,试问点![]() 到直线
到直线![]() 的距离是否为定值,证明你的结论.
的距离是否为定值,证明你的结论.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com