Question

【题目】已知命题p：函数 在（﹣∞，+∞）上有极值，命题q：双曲线 的离心率e∈（1，2）．若p∨q是真命题，p∧q是假命题，求实数a的取值范围．

Answer 1

【答案】解：命题p：f′（x）=3x2+2ax+a+ ，
∵函数f（x）在（﹣∞，+∞）上有极值，
∴f′（x）=0有两个不等实数根，
∴△=4a2﹣4×3（a+ ）=4a2﹣4（3a+4）＞0，
解得a＞4或a＜﹣1；
命题q：双曲线 的离心率e∈（1，2），为真命题，
则 ∈（1，2），解得0＜a＜15．
∵命题“p∧q”为假命题，“p∨q”为真命题，
∴p与q必然一真一假，
则 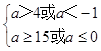或 ，
解得：a≥15或0＜a≤4或a＜﹣1
【解析】分别求出p，q为真时的a的范围，由于命题“p∧q”为假命题，“p∨q”为真命题，可得p与q必然一真一假．即可得出．
【考点精析】通过灵活运用复合命题的真假，掌握“或”、 “且”、 “非”的真值判断:“非p”形式复合命题的真假与F的真假相反；“p且q”形式复合命题当P与q同为真时为真，其他情况时为假；“p或q”形式复合命题当p与q同为假时为假，其他情况时为真即可以解答此题．