
【题目】
【答案】(1)![]() ,极小值为
,极小值为![]() 无极大值;(2)见解析;(3)见解析.
无极大值;(2)见解析;(3)见解析.
【解析】试题分析:(1)求导,由![]() ,由导数工具求得极值;(2)令,
,由导数工具求得极值;(2)令, ![]() ;(3)解法一:①若
;(3)解法一:①若![]() ,由(2)得,存在
,由(2)得,存在![]() 使得命题恒成立.②若
使得命题恒成立.②若![]() ,令
,令![]() ,命题转化为
,命题转化为![]() 成立,即只要
成立,即只要![]() 成立.令
成立.令![]() ,利用导数工具得:取
,利用导数工具得:取![]() ,
, ![]() .即存在
.即存在![]() ,使得原命题成立. 解法二:对任意给定的正数c,取
,使得原命题成立. 解法二:对任意给定的正数c,取![]() 由(2)知,当x>0时,
由(2)知,当x>0时, ![]()
![]() 当
当![]() 时,
时, ![]()
![]()
![]() ,故对任意给定的正数c,总存在
,故对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
试题解析:
(1)由![]() ,得
,得![]() .又
.又![]() ,得
,得![]() .所以
.所以
![]() .令
.令![]() ,得
,得![]() .当
.当![]() 时,
时, ![]() 单
单
调递减;当![]() 时,
时, ![]() 单调递增.所以当
单调递增.所以当![]() 时,
时, ![]() 取得极小值,且极
取得极小值,且极
小值为![]() 无极大值.
无极大值.
(2)令![]() ,则
,则![]() .由(I)得
.由(I)得![]() ,故
,故![]() 在R上单调递增,又
在R上单调递增,又![]() ,因此,当
,因此,当![]() 时,
时, ![]() ,即
,即![]() ,
,
(3)解法一:①若![]() ,则
,则![]() .又由(II)知,当
.又由(II)知,当![]() 时,
时, ![]() .所以当
.所以当![]() 时,
时, ![]() .取
.取![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
②若![]() ,令
,令![]() ,要使不等式
,要使不等式![]() 成立,只要
成立,只要![]() 成立.而要使
成立.而要使![]() 成立,则只要
成立,则只要![]() ,只要
,只要![]() 成立.令
成立.令![]() ,则
,则![]() .所以当
.所以当![]() 时,
时, ![]() 在
在![]() 内单调递增.取
内单调递增.取![]() ,所以
,所以![]() 在
在![]() 内单调递增.又
内单调递增.又![]() .易知
.易知![]() .所以
.所以![]() .即存在
.即存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
综上,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.
解法二:对任意给定的正数c,取![]()
由(2)知,当x>0时, ![]() ,所以
,所以![]()
当![]() 时,
时, ![]()
因此,对任意给定的正数c,总存在![]() ,当
,当![]() 时,恒有
时,恒有![]() .
.


科目:高中数学 来源: 题型:
【题目】有一种新型的洗衣液,去污速度特别快.已知每投放k(1≤k≤4,且k∈R)个单位的洗衣液在一定量水的洗衣机中,它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y=k·f(x),其中f(x)=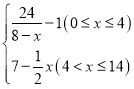 若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
若多次投放,则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和.根据经验,当水中洗衣液的浓度不低于4(克/升)时,它才能起到有效去污的作用.
(1)若只投放一次k个单位的洗衣液,两分钟时水中洗衣液的浓度为3(克/升),求k的值;
(2)若只投放一次4个单位的洗衣液,则有效去污时间可达几分钟?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)=2sin(x-![]() )-
)-![]() ,现将f(x)的图象向左平移
,现将f(x)的图象向左平移![]() 个单位长度,再向上平移
个单位长度,再向上平移![]() 个单位长度,得到函数g(x)的图象.
个单位长度,得到函数g(x)的图象.
(1)求f(![]() )+g(
)+g(![]() )的值;
)的值;
(2)若a,b,c分别是△ABC三个内角A,B,C的对边,a+c=4,且当x=B时,g(x)取得最大值,求b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
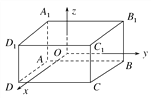
【题目】如图,已知长方体ABCD-A1B1C1D1的对称中心在坐标原点,交于同一顶点的三个面分别平行于三个坐标平面,顶点A(-2,-3,-1),求其他七个顶点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-8y+12=0,直线l经过点D(-2,0),且斜率为k.
(1)求以线段CD为直径的圆E的方程.
(2)若直线l与圆C相离,求k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点的零件的多少随机器的运转的速度的变化而变化,下表为抽样试验的结果:
转速 | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数 | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果![]() 对
对![]() 有线性相关关系,请画出一条直线近似地表示这种线性关系;
有线性相关关系,请画出一条直线近似地表示这种线性关系;
(3)在实际生产中,若它们的近似方程为![]() ,允许每小时生产的产品中有缺点的零件最多为
,允许每小时生产的产品中有缺点的零件最多为![]() 件,那么机器的运转速度应控制在什么范围内?
件,那么机器的运转速度应控制在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com