练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在三棱锥中，，平面和平面所成角为，则三棱锥外接球的体积为（ ）

    A. B. C. D.

    【答案】A

    【解析】分析：先明确球心的位置：过△ABC的外心作平面ABC的垂线，过△PBC的外心作平面PBC的垂线，设两条垂线交于点O，则O为三棱锥外接球的球心,然后把问题转化为解三角形的问题.

    详解：如图，过△ABC的外心作平面ABC的垂线，过△PBC的外心作平面PBC的垂线，设两条垂线交于点O，则O为三棱锥外接球的球心，过点作，连接，则BC⊥平面，BC⊥平面，所以四点共面，所以BC⊥,

    由BC⊥，BC⊥，所以∠为平面PBC和平面ABC所成角，即∠，

    由，得，由余弦定理得，

    由正弦定理得，即，又因为，所以由余弦定理得，所以，所以，三棱锥外接球的体积为

    故选：A

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某企业在第年年初购买一台价值为万元的设备，的价值在使用过程中逐年减少从第年到第年，每年年初的价值比上年年初减少万元；从第年开始，每年年初的价值为上年年初的.

    (1)求第年年初的价值的表达式．

    (2)设，若大于万，则继续使用；否则，必须在第年年初对更新．

    ①求；

    ②证明：必须在第年年初对更新．（若是递减数列，也是递减数列）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】“微信运动”是手机推出的多款健康运动软件中的一款，杨老师的微信朋友圈内有位好友参与了“微信运动”，他随机选取了位微信好友（女人，男人），统计其在某一天的走路步数.其中，女性好友的走路步数数据记录如下：

    5860 8520 7326 6798 7325 8430 3216 7453 11754 9860

    8753 6450 7290 4850 10223 9763 7988 9176 6421 5980

    男性好友走路的步数情况可分为五个类别： 步)(说明:“”表示大于等于,小于等于.下同), 步), 步), 步), 步及以),且三种类别人数比例为,将统计结果绘制如图所示的条形图.

    若某人一天的走路步数超过步被系统认定为“卫健型",否则被系统认定为“进步型”.

    （1）若以杨老师选取的好友当天行走步数的频率分布来估计所有微信好友每日走路步数的概率分布,请估计杨老师的微信好友圈里参与“微信运动”的名好友中,每天走路步数在步的人数；

    （2）请根据选取的样本数据完成下面的列联表并据此判断能否有以上的把握认定“认定类型”与“性别”有关?

    卫健型

    进步型

    总计

    男

    20

    女

    20

    总计

    40

    （3）若从杨老师当天选取的步数大于10000的好友中按男女比例分层选取人进行身体状况调查，然后再从这位好友中选取人进行访谈，求至少有一位女性好友的概率.

    附： ，

    0.10

    0.05

    0.025

    0.010

    2.706

    3.841

    5.024

    6.635

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知平面上动点到点的距离与到直线的距离之比为，记动点的轨迹为曲线.

    （1）求曲线的方程；

    （2）设是曲线上的动点，直线的方程为.

    ①设直线与圆交于不同两点， ，求的取值范围；

    ②求与动直线恒相切的定椭圆的方程；并探究：若是曲线： 上的动点，是否存在直线： 恒相切的定曲线？若存在，直接写出曲线的方程；若不存在，说明理由.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数

    （1）若曲线在点处的切线为， 与轴的交点坐标为，求的值；

    （2）讨论的单调性.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P－ABCD的底面是矩形，侧面PAD为等边三角形，AB＝，AD＝， PB＝.

    （1）求证：平面PAD⊥平面ABCD；

    （2）M是棱PD上一点，三棱锥M－ABC的体积为1.记三棱锥P－MAC的体积为，三棱锥M－ACD的体积为，求.

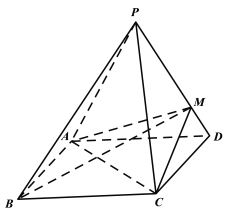
    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】据统计，在不考虑其他因素的条件下，某段下水道的排水量V（单位：立方米/小时）是垃圾杂物密度x（单位：千克/立方米）的函数。当下水道的垃圾杂物密度达到3千克/立方米时，会造成堵塞，此时排水量为0；当垃圾杂物密度不超过0.5千克/立方米时，排水量是80立方米/小时。研究表明，当时，排水量V是垃圾杂物密度x的一次函数.

    （1）当时，求函数的解析式；

    （2）当垃圾杂物密度x为多大时，垃圾杂物量（单位时间内通过某段下水道的垃圾杂物量，单位：千克/小时）可以达到最大？求出这个最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩，按成绩分组，得到的频率分布表如下：

    组号

    分组

    频率

    第1组

    [160，165)

    0.05

    第2组

    [165，170)

    0.35

    第3组

    [170，175)

    ①

    第4组

    [175，180)

    0.20

    第5组

    [180，185]

    0.10

    (1)请先求出频率分布表中①处应填写的数据，并完成如图所示的频率分布直方图；

    (2)为了能选拔出最优秀的学生，高校决定在笔试成绩高的第3，4，5组中用分层抽样的方法抽取6名学生进入第二轮面试，求第3，4，5组每组各应抽取多少名学生进入第二轮面试．

    (3)根据直方图估计这次自主招生考试笔试成绩的平均数和中位数；

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】青岛二中有羽毛球社乒乓球社和篮球社,三个社团的人数分别为27,9,18,现采用分层抽样的方法从这三个社团中抽取6人参加活动.

    (1)求应从这三个社团中分别抽取的学生人数;

    (2)将抽取的6名学生进行编号,编号分别为,,,,,,从这6名学生中随机抽出2名参加体育测试.

    ①用所给的编号列出所有可能的结果;

    ②设事件是“编号为,的两名学生至少有一人被抽到”,求事件发生的概率.

    查看答案和解析>>

    同步练习册答案