
 已知
已知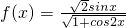 ,
,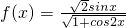 的解析式可得
的解析式可得 ,k∈Z}关于原点对称
,k∈Z}关于原点对称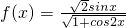 =
=
 =-
=- =-f(x)
=-f(x)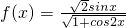 为奇函数..(4分)
为奇函数..(4分)

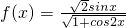 在(
在( )递增,在[
)递增,在[ )及(
)及(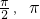 ]递减
]递减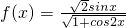 ,我们可以先求出函数的定义域A,验证A是否关于原点对称,若对称,再判断f(-x)与f(x)的关系,然后根据函数奇偶性的定义得到结论.
,我们可以先求出函数的定义域A,验证A是否关于原点对称,若对称,再判断f(-x)与f(x)的关系,然后根据函数奇偶性的定义得到结论.

科目:高中数学 来源:2009-2010学年湖北省孝感高中高一(上)期末数学试卷(解析版) 题型:解答题
 ,
,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com