
如图,制图工程师要用两个同中心的边长均为4的正方形合成一个八角形图形.由对称性,图中8个三角形都是全等的三角形,设 .
.
(1)试用 表示
表示 的面积;
的面积;
(2)求八角形所覆盖面积的最大值,并指出此时 的大小.
的大小.
(1)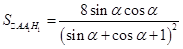 ;(2)
;(2)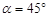 时面积的最大值为
时面积的最大值为 .
.
解析试题分析:(1)要求 的面积,关键是求出两直角边长,因此我们要把这两直角边与正方形的边长联系起来,由已知,
的面积,关键是求出两直角边长,因此我们要把这两直角边与正方形的边长联系起来,由已知, ,从而直
,从而直 的三边长之和为正方形的边长4,所以
的三边长之和为正方形的边长4,所以 的边长可以用
的边长可以用 表示,也就求出了它的面积;(2)由(1)
表示,也就求出了它的面积;(2)由(1)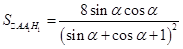 ,要求这个式子的最大值,我们要用换元法变形,这里我们设
,要求这个式子的最大值,我们要用换元法变形,这里我们设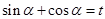 ,则
,则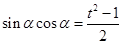 ,于是
,于是 就变为
就变为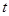 的代数函数
的代数函数 ,不能忘记的是
,不能忘记的是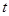 的范围是
的范围是 ,
,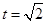 时
时 取最大值.
取最大值.
试题解析:(1)设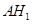 为
为 ,∴
,∴ ,
,  , 3分
, 3分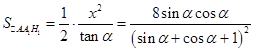 ,
, , 7分
, 7分
(2)令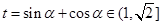 , 9分
, 9分
只需考虑 取到最大值的情况,即为
取到最大值的情况,即为 , 11分
, 11分
当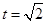 , 即
, 即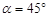 时,
时,  达到最大 13分
达到最大 13分
此时八角形所覆盖面积的最大值为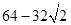 . 14分
. 14分
考点:(1)方程与三角形面积;(2)换元法与三角函数的最大值.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:高中数学 来源: 题型:解答题
在△ABC中,内角A,B,C所对的边分别是a,b,c.已知bsinA=3csinB,a=3,cosB= .
.
(1)求b的值;
(2)求sin(2B- )的值.
)的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C的对边分别为a,b,c,已知角A= , sin B=3sin C.
, sin B=3sin C.
(1)求tan C的值;
(2)若a= ,求△ABC的面积.
,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
辽宁广播电视塔位于沈阳市沈河区青年公园西侧,蜿蜒的南运河带状公园内,占地8000平方米.全塔分为塔座、塔身、塔楼和桅杆四部分.某数学活动小组在青年公园内的A处测得塔顶B处的仰角为45°. 在水平地面上,沿着A点与塔底中心C处连成的直线行走129米后到达D处(假设可以到达),此时测得塔顶B处的仰角为60°.
(1)请你根据题意,画出一个ABCD四点间的简单关系图形;
(2)根据测量结果,计算辽宁广播电视塔的高度(精确到1米).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A、B、C所对的边分别为a、b、c,且b2+c2=a2+bc.
(1)求角A的大小;(2)若sinB·sinC=sin2A,试判断△ABC的形状.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在△ABC中,角A,B,C对应的边分别是a,b,c.已知cos 2A-3cos(B+C)=1.
(1)求角A的大小;
(2)若△ABC的面积S=5 ,b=5,求sin Bsin C的值.
,b=5,求sin Bsin C的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com