
【题目】如图1,四边形![]() 为直角梯形,
为直角梯形,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,
上一点,![]() 为
为![]() 的中点,且
的中点,且![]() ,
,![]() ,现将梯形沿
,现将梯形沿![]() 折叠(如图2),使平面
折叠(如图2),使平面![]() 平面
平面![]() .
.

(1)求证:平面![]()
![]() 平面
平面![]() .
.
(2)能否在边![]() 上找到一点
上找到一点![]() (端点除外)使平面
(端点除外)使平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ?若存在,试确定点
?若存在,试确定点![]() 的位置,若不存在,请说明理由.
的位置,若不存在,请说明理由.
【答案】(1)证明见解析.(2)存在点,![]() 为线段
为线段![]() 中点
中点
【解析】
(1)根据线面垂直的判定定理和面面垂直的判定定理,即可证得平面![]()
![]() 平面
平面![]() ;
;
(2)以![]() 为坐标原点建立如图所示的空间直角坐标系,求得平面
为坐标原点建立如图所示的空间直角坐标系,求得平面![]() 和平面
和平面![]() 的法向量,利用向量的夹角公式,即可求解.
的法向量,利用向量的夹角公式,即可求解.
(1)在直角梯形![]() 中,作于
中,作于![]() 于
于![]() ,连接
,连接![]() ,
,
则![]() ,
,![]() ,则
,则![]() ,
,![]() ,
,
则![]() ,
,
在直角![]() 中,可得
中,可得![]() ,
,
则![]() ,
,
所以![]() ,
,
故![]() ,且折叠后
,且折叠后![]() 与
与![]() 位置关系不变.
位置关系不变.
又因为平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]()
![]()
![]() ,
,
所以![]() 平面
平面![]() ,
,
因为![]()
![]() 平面
平面![]() ,所以平面
,所以平面![]()
![]() 平面
平面![]() .
.
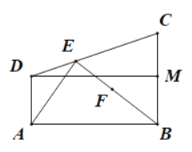
(2)在![]() 中,由
中,由![]() ,
,![]() 为
为![]() 的中点,可得
的中点,可得![]() .
.
又因为平面![]()
![]() 平面
平面![]() ,且平面
,且平面![]()
![]() 平面
平面![]()
![]()
![]() ,
,
所以![]()
![]() 平面
平面![]() ,则以
,则以![]() 为坐标原点建立如图所示的空间直角坐标系,
为坐标原点建立如图所示的空间直角坐标系,
则![]() ,
,![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,则
,则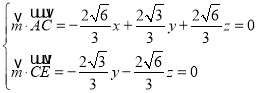 ,
,
令![]() ,可得平面
,可得平面![]() 的法向量为
的法向量为![]() ,
,
假设![]() 存在点
存在点![]() 使平面
使平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() ,且
,且![]() (
(![]() ),
),
∵![]() ,∴
,∴![]() ,故
,故![]() ,
,
又![]() ,∴
,∴![]() ,
,
又由![]() ,
,
设平面![]() 的法向量为
的法向量为![]() ,可得
,可得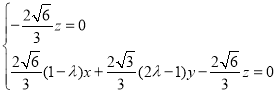 ,
,
令![]() 得
得![]() ,
,
∴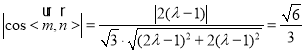 ,解得
,解得![]() ,
,
因此存在点![]() 且
且![]() 为线段
为线段![]() 中点时使平面
中点时使平面![]() 与平面
与平面![]() 所成角的余弦值为
所成角的余弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,抛物线
,抛物线![]() 上的点到准线的最小距离为2.
上的点到准线的最小距离为2.
(1)求抛物线![]() 的方程;
的方程;
(2)若过点![]() 作互相垂直的两条直线
作互相垂直的两条直线![]() ,
,![]() ,
,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,
两点,![]() ,
,![]() 分别为弦
分别为弦![]() ,
,![]() 的中点,求
的中点,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“中国式过马路”存在很大的交通安全隐患,某调查机构为了解路人对“中国式过马路”的态度是否与性别有关,从马路旁随机抽取30名路人进行了问卷调查,得到了如图的![]() 列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是
列联表.已知在这30人中随机抽取1人抽到反感“中国式过马路”的路人的概率是![]() .
.
(1)求![]() 列联表中的
列联表中的![]() ,
,![]() 的值;
的值;
男性 | 女性 | 合计 | |
反感 | 10 |
|
|
不反感 |
| 8 |
|
合计 |
|
| 30 |
(2)根据列联表中的数据,判断是否有95%把握认为反感“中国式过马路”与性别有关?
临界值表:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
参考公式: ,
,![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】新闻出版业不断推进供给侧结构性改革,深入推动优化升级和融合发展,持续提高优质出口产品供给,实现了行业的良性发展.下面是2012年至2016年我国新闻出版业和数字出版业营收增长情况,则下列说法错误的是( )
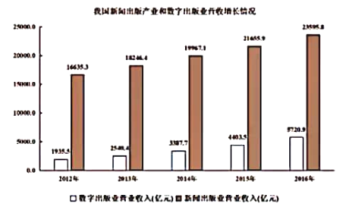
A. 2012年至2016年我国新闻出版业和数字出版业营收均逐年增加
B. 2016年我国数字出版业营收超过2012年我国数字出版业营收的2倍
C. 2016年我国新闻出版业营收超过2012年我国新闻出版业营收的1.5倍
D. 2016年我国数字出版营收占新闻出版营收的比例未超过三分之一
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() (
(![]() )的一个焦点为
)的一个焦点为![]() ,点
,点![]() 在C上.
在C上.
(1)求椭圆C的方程;
(2)过点![]() 且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为
且斜率不为0的直线l与椭圆C相交于M,N两点,椭圆长轴的两个端点分别为![]() ,
,![]() ,
,![]() 与
与![]() 相交于点Q,求证:点Q在某条定直线上.
相交于点Q,求证:点Q在某条定直线上.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场举行有奖促销活动,顾客购买一定金额商品后即可抽奖,每次抽奖都从装有4个红球、6个白球的甲箱和装有5个红球、5个白球的乙箱中,各随机摸出1个球,在摸出的2个球中,若都是红球,则获一等奖;若只有1个红球,则获二等奖;若没有红球,则不获奖.
(1)求顾客抽奖1次能获奖的概率;
(2)若某顾客有3次抽奖机会,记该顾客在3次抽奖中获一等奖的次数为![]() ,求
,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆G:![]() 的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
的右焦点为F,过F的直线l交椭圆于A、B两点,直线与l不与坐标轴平行,若AB的中点为N,O为坐标原点,直线ON交直线x=3于点M.
(1)求证:MF⊥l;
(2)求![]() 的最大值,
的最大值,
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com