一支步枪的发射速度为v0,有人每隔1s竖直向上打一枪,若不计空气阻力,求第一颗子弹射出后与第n(n≥2)颗射出的子弹彼此相遇的时间.(设子弹不相碰,且都在空中运动).
见分析
【试题分析】
【解析】根据题意可知,每颗子弹射出后都在做竖直上抛运动.由于初速度相同,所以每颗子弹的上升时间与下降时间都相等,则第一颗子弹必然在下降过程中与第n颗子弹在上升过程中相遇.
解法1:从第一颗子弹射出的时刻开始计时,设相遇第一颗子弹运动了ts.因为每隔1s发射一颗子弹,所以相遇时第n颗子弹运动的时间为
t
n=[t-(n-1)]①
由相遇时位移相等得 h
1=h
n②
又因为 h
1=v
0t-
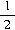
gt
2③
h
n=v
0t
n-
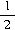
g
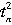
④
所以,将①、②、④式代入②式得: t=
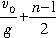
,(n≥2)
解法2:根据竖直上抛运动的特点可知:相遇时第n颗子弹与第一颗子弹的速度大小相等、方向相反,即 v
n=-v
1 ①
又因为 v
1=v
0-gt ②
v
n=v
0-gt
n ③
t
n=[t-(n-1)]④
所以,将②、③、④式代入①式得: t=
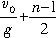
,(n≥2)
解法3:根据竖直上抛运动的特点可知:相遇时第n颗子弹与第一颗子弹运动的时间之和等于
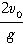
,即 t+t
n=
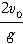
①
又因为 t
n=[t-(n-1)] ②
所以,将(2)式代入(1)式得: t=

,(n≥2)
解法4:因为相遇时第一颗子弹比第n颗子弹多运动了(n-1)s,所以根据竖直上抛运动的对称性可知:第一颗子弹从最高点下降到相遇点所经历的时间为1s,则相遇时第一颗子弹运动的时间为
t=t
上+
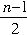
①
又因为 t
上=
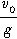
②
t=
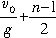
,(n≥2)

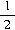 gt2③
gt2③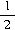 g
g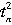 ④
④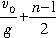 ,(n≥2)
,(n≥2)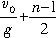 ,(n≥2)
,(n≥2)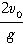 ,即 t+tn=
,即 t+tn=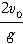 ①
① ,(n≥2)
,(n≥2)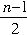 ①
①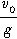 ②
②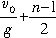 ,(n≥2)
,(n≥2) 
