练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    如图所示，在纸面内半径为R的圆形区域中充满了垂直于纸面向里、磁感应强度为B的匀强磁场，一点电荷从图中A点以速度v垂直磁场射入，当该电荷离开磁场时，速度方向刚好改变了180°，不计电荷的重力，下列说法正确的是（ ）

    A．该点电荷离开磁场时速度方向的反向延长线通过O点
    B．该点电荷的比荷为
    C．该点电荷在磁场中的运动时间t=
    D．该点电荷带正电
    【答案】分析：根据电荷在磁场中偏转180°和电荷在磁场中在洛伦兹力作用下做匀速圆周运动作出电荷在磁场中的运运轨迹，根据已知条件由几何关系和洛伦兹力提供向心力推导即可．
    解答：解：如图所示，点电荷在磁场中做匀速圆周运动，根据几何关系作出点电荷运动轨迹有：

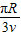
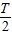    电荷在电场中刚好运动，电荷做圆周运动的半径r=Rsin30°所以有：
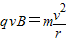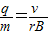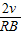    A、如图，电荷离开磁场时速度方向与进入磁场时速度方向相反，其反向延长线不通过O点，故A错误；
    B、根据洛伦兹力提供向心力有?=，故B正确；
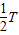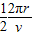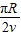    C、由图知该电荷在磁场中运动的时间t===，所以C错误；
    D、根据电荷偏转方向由洛伦兹力方向判定该电荷带负电，故D错误．
    故选B．
    点评：正确的判断带电粒子在磁场中的运动轨迹，利用几何关系求运动半径，洛伦兹力提供向心力是解决本题的关键．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：

    如图所示，在xoy平面内，直线MN与x轴正方向成30°角，MN下方是垂直于纸面向外的匀强磁场，MN与y轴正方向间存在电场强度E=
    4
    3
    ×105N/C的匀强电场，其方向与y轴正方向成60°角且指向左上方，一重力不计的带正电粒子，从坐标原点O沿x轴正方向进入磁场，已知粒子的比荷
    q
    m
    =107C/kg，结果均保留两位有效数字，试问：
    （1）若测得该粒子经过磁场的时间t1=
    π
    3
    ×10-6s    ，求磁感应强度的大小B；
    （2）若测得该粒子经过磁场的时间t1=
    π
    3
    ×10-6s    ，粒子从坐标原点开始到第一次到达y轴正半轴的时间t
    （3）若粒子的速度v0=1.0×106m/s，求粒子进入电场后最终离开电场时的位置坐标．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    在xoy竖直平面内，仅在第一、四象限分布着竖直向上的匀强电场E，第一象限还存在着垂直纸面向里的匀强磁场B，方向如图所示．在y轴负向A点处有一质量为1.0×10-6 kg，电量为q=1.0×10-6 c的带正电微粒以初速度v0=8m/s，垂直y轴射入第四象限内．其中电场强度E=20N/c，OA的长为d=1.8m，g取10m/s2．
    （1）微粒将打在x轴的P点，求OP的长l；
    （2）如果带电微粒在P点进入第一象限，刚好与一质量也为m、不带电的微粒碰撞粘合在一起，形成一个新带电微粒，新微粒的质量为2m，电量为q，速度大小变为原来的一半，方向不变，则要使新微粒能再次打到x轴的正半轴上，则磁感应强度B应满足什么条件？

    查看答案和解析>>

    科目：高中物理 来源： 题型：

    （2012?无锡二模）如图所示，在光滑的水平面上有一直角坐标系Oxy．现有一个质量m=O．lkg．带电荷量q=一2×10-4C的微粒，从y轴正半轴上的P1点以速度v0=0.6m/s垂直于y轴射入．已知在y＞0的空间内有与y轴方向平行的匀强电场，在y＜0的空间内存在方向与纸面垂直的匀强磁场．带电微粒从P1点射入电场后，经坐标（1.2，0）的P2点与x轴正方向成53°角射入y＜0的空间，最后从y轴负半轴上的P3点垂直于y轴射出．（已知：sin53=0.8，cos53°=0.6）求：
    （1）P1点的坐标；
    （2）匀强电场的电场强度E；
    （3）匀强磁场的磁感应强度B．

    查看答案和解析>>

    科目：高中物理 来源： 题型：

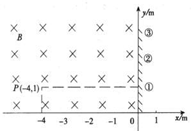    精英家教网如图所示，在直角坐标系的第二象限内有垂直纸面向里的匀强磁场，磁感应强度的大小为0.1T，在y轴的正半轴上竖有一挡板，板足够长，挡板平面垂直于纸面．在P（-4，1）点有一粒子放射源，能连续地向各个方向放射出速率相同的同种带正电粒子，粒子的质量m=1.0×10ˉ6kg，带电荷量为q=+1×10ˉ5 C，不计粒子重力，求（结果保留两位有效数字）：
    （1）要使粒子能够击中挡板，粒子的速度至少为多大？
    （2）若粒子的速度大小为3m/s，求粒子击中挡板的最高点距0点的距离．

    查看答案和解析>>

    科目：高中物理 来源：2012-2013学年福建省高三上期末考试物理试卷（解析版） 题型：计算题

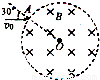
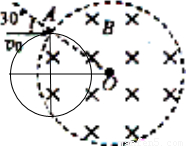
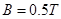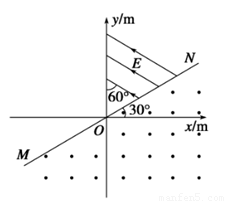
    (12分)如图所示，在xoy平面内，直线MN与x轴正方向成30o角，MN下方是垂直于纸面向外的匀强磁场，MN与y轴正方向间存在电场强度E=×105N/C的匀强电场，其方向与y轴正方向成60o角且指向左上方，一重力不计的带正电粒子，从坐标原点O沿x轴正方向进入磁场，已知粒子的比荷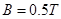=107C/kg，结果均保留两位有效数字，试问：

    （1）若测得该粒子经过磁场的时间t1=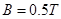，求磁感应强度的大小B；

    （2）若测得该粒子经过磁场的时间t1=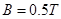，粒子从坐标原点开始到第一次到达y轴正半轴的时间t

    （3）若粒子的速度v0=1.0×106m/s，求粒子进入电场后最终离开电场时的位置坐标

     

    查看答案和解析>>

    同步练习册答案