
 ;
; ,
,
 ;
;

 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中物理 来源: 题型:
查看答案和解析>>
科目:高中物理 来源: 题型:
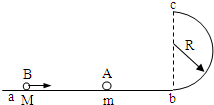 (2008?茂名一模)如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求:
(2008?茂名一模)如图所示,abc是光滑的轨道,其中ab是水平的,bc为与ab相切的位于竖直平面内的半圆,半径R=0.30m.质量m=0.20kg的小球A静止在轨道上,另一质量M=0.60kg、速度V0=5.5m/s的小球B与小球A正碰.已知相碰后小球A经过半圆的最高点c落到轨道上距b点为L=4R处,重力加速度g取10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:
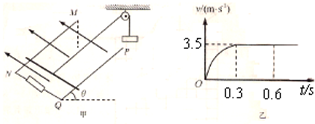 如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=3.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=300.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的
如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=3.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=300.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的| 1 | 3 |
查看答案和解析>>
科目:高中物理 来源: 题型:
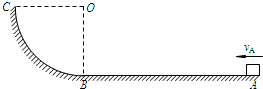 (2011?西城区一模)如图,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑块的质量m=0.60kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑块离开C点后竖直上升h=0.20m,取g=10m/s2.求:
(2011?西城区一模)如图,一滑块经水平轨道AB,进入竖直平面内的四分之一圆弧轨道BC.已知滑块的质量m=0.60kg,在A点的速度vA=8.0m/s,AB长x=5.0m,滑块与水平轨道间的动摩擦因数μ=0.15,圆弧轨道的半径R=2.0m,滑块离开C点后竖直上升h=0.20m,取g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:
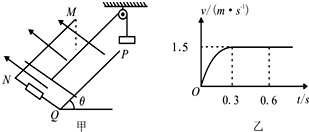 如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=1.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=30°.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的
如图甲所示,一足够长阻值不计的光滑平行金属导轨MN、PQ之间的距离L=1.0m,NQ两端连接阻值R=1.0Ω的电阻,磁感应强度为B的匀强磁场垂直于导轨所在平面向上,导轨平面与水平面间的夹角θ=30°.一质量m=0.20kg,阻值r=0.50Ω的金属棒垂直于导轨放置并用绝缘细线通过光滑的定滑轮与质量M=0.60kg的重物相连.细线与金属导轨平行.金属棒沿导轨向上滑行的速度v与时间t之间的关系如图乙所示,已知金属棒在0~0.3s内通过的电量是0.3~0.6s内通过电量的| 2 | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com