
1.下列有关数列的表述:①数列的通项公式是唯一的;②数列0,1,0,-1与数列-1,0,1,0是相同的数列;③数列若用图象表示,它是一群孤立的点;④数列中的数是按一定次序排列的.其中说法正确的是________.
2.如果数列{an}(an∈R)对任意m,n∈N*均满足am+n=aman,且a3=8,那么a10=________.
3.若a1=3,an=an-1+(n≥2),bn=,则数列{bn}的第3项是________.
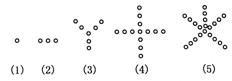
4.根据下面5个图形及相应点的个数的变化规律,猜测第n个图中有________个点.
5.已知数列{an}的通项公式是an=n2+kn+2,若对于n∈N*,都有an+1>an成立,则实数k的取值范围是________.
6.如果等差数列{an}中,a3+a4+a5=12,那么a1+a2+…+a7等于________.
7.已知等差数列{an}的前n项和为Sn,且满足-=1,则数列{an}的公差是________.
8.等比数列a+log23,a+log43,a+log163的公比是________.
9.已知{an}是首项为1的等比数列,Sn是{an}的前n项和,且9S3=S6,则数列{}的前5项和为________.
10.已知数列{an}为等差数列,若<-1,则数列{|an|}的最小项是第________项.
11.等比数列{an}的公比q>0,已知a2=1,am+2+am+1=6am,则{an}的前4项和是________.
12.设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0,则d的取值范围是________.
13.一直角三角形三边的长成等比数列,则较小锐角的正弦值为________.
14.已知{an}是递减等比数列,a2=2,a1+a3=5,则a1a2+a2a3+…+anan+1(n∈N*)的取值范围是________.
15.(本小题满分14分)
已知数列{an}满足a1=2,an+1=(n∈N*),求a1a2a3…a2011a2012的值.
16.(本小题满分14分)
已知等差数列{an}满足a4=6,a6=10.
(1)求数列{an}的通项公式;
(2)设等比数列{bn}的各项均为正数,其前n项和Tn,若b3=a3,T2=3,求Tn.
17.(本小题满分14分)
已知数列{an}满足a1=1,a2=-13,an+2-2an+1+an=2n-6.
(1)设bn=an+1-an,求数列{bn}的通项公式;
(2)求n为何值时,an最小.
18.(本小题满分14分)
在等差数列{an}中,a16+a17+a18=a9=-18,其前n项的和为Sn,
(1)求Sn的最小值,并求出Sn取最小值时n的值;
(2)求Tn=|a1|+|a2|+…+|an|.
19.(本小题满分16分)
已知数列{an}中,a1=2,a2=4,an+1=3an-2an-1(n≥2,n∈N*).
(1)证明:数列{an+1-an}是等比数列,并求出数列{an}的通项公式;
(2)记bn=(n∈N*),求数列{bn}的前n项和Sn.
20.(本小题满分16分)
设数列{an}的前n项和为Sn,已知a1=a,an+1=Sn+3n,n∈N*.
(1)设bn=Sn-3n,求数列{bn}的通项公式;
(2)若an+1≥an,n∈N*,求a的取值范围.
数列(1)参考答案
二参考答案
一、填空题:
1.答案:③④ 解析:如果数列{an}的第n项an与n之间的关系可以用一个公式来表示,那么这个公式就叫做这个数列的通项公式,但一个数列可以没有通项公式,也可以有几个通项公式,如:数列1,-1,1,-1,1,-1,…的通项公式可以是an=(-1)n+1,也可以是an=cos(n-1)p,故①错;由数列的概念知数列0,1,0,-1与数列-1,0,1,0是不同的数列,故②错;易知③④是正确的.
2.答案:1 024 解析:由题意知,a2=a,a3=a1a2=a⇒a1=2,a2=4,以此类推可得a10=210=1 024.
3. 答案: 解析:∵a1=3,an=an-1+(n≥2),∴a2=a1+=3+ =,a3=a2+=+=+=. ∵bn=,∴b3= = .
4. 答案:n2-n+1 解析:观察图中5个图形点的个数分别为1,1´2+1,2´3+1,3´4+1,4´5+1,故第n个图中点的个数为(n-1)´n+1=n2-n+1.
5. 答案:k>-3 解析:由an+1>an得(n+1)2+k(n+1)+2>n2+kn+2,∴k>-(2n+1),∴k>-3.
6. 答案:28 解析:∵a3+a4+a5=12,∴a4=4.∴a1+a2+…+a7==7a4=28.
7. 答案:2 解析:∵Sn=,∴=,由-=1得,-=1,即a3-a2=2,∴数列{an}的公差为2.
8. 答案: 解析:由已知得:(a+log43)2=(a+log23)(a+log163)
∴2alog43+(log43)2=(log23+log163)a+log23log163,∴2alog43+2=(log23+log23)a+(log23)2,
∴2a×log23=a,∴a=0,∴公比为==.
9. 答案: 解析:易知公比q≠1,由9S3=S6得9=,解得q=2,
∴{}是首项为1,公比为的等比数列,∴其前5项和为=.
10. 答案:6 解析:设等差数列{an}的公差为d,则由已知结合通项公式得<-1,即(a1+5d)(2a1+9d)<0,所以(a1+5d)×<0;分公差d的正负讨论,得:当d>0时,此时a5=a1+4d<a1+d<0,a6=a1+5d>0,故数列{|an|}的最小项只能是|a5|或|a6|,而|a6|-|a5|=(a1+5d)-[-(a1+4d)]=2a1+9d<0,故所求最小项是|a6|,即第6项;当d<0时,同样讨论可得.
11.答案: 解析:由已知条件am+2+am+1=6am可得a2qm+a2qm-1=6a2qm-2,即得q2+q-6=0,解得q=2或q=-3(舍去),则数列{an}的前四项的和为+1+2+4=.
12.答案:(-∞,-2]∪[2,+∞) 解析:∵S5S6+15=0,∴(5a1+10d)(6a1+15d)+15=0,即
2a+9da1+10d2+1=0.故(4a1+9d)2=d2-8,∴d2≥8,则d的取值范围是(-∞,-2]∪[2,+∞).
13. 答案: 解析:设三边a,b,c成等比数列,且a<b<c,
则b2=ac,且c2=a2+b2,∴ac=c2-a2,即=1-.
∵sin A=,∴sin2A+sin A-1=0,解得sin A=.
14.答案: 解析:∵a2=2,a1+a3=5,∴+2q=5,∵{an}递减,∴q=,a1=4,
∵数列{anan+1}是以a1a2为首项,q2为公比的等比数列,
∴a1a2+a2a3+…+anan+1===,
而是递增数列,≤1-n<1,∴8≤<.
二、解答题:
15.解:∵a1=2,an+1=,∴a2=-3,a3=-,a4=,a5=2,
∴数列{an}的周期为4,且a1a2a3a4=1,∴a1a2a3a4…a2011a2012=1.
16.解:(1)设等差数列{an}的公差为d,首项为a1,
∵a4=6,a6=10,∴解得
∴数列{an}的通项公式an=a1+(n-1)d=2n-2.
(2)设各项均为正数的等比数列{bn}的公比为q(q>0).
∵an=2n-2,∴a3=4,
解得q=2,b1=1或(舍去)
∴Tn===2n-1.
17.解: (1)由an+2-2an+1+an=2n-6得:(an+2-an+1)-(an+1-an)=2n-6,
∴bn+1-bn=2n-6.
当n≥2时,bn-bn-1=2(n-1)-6,bn-1-bn-2=2(n-2)-6,
b3-b2=2×2-6,b2-b1=2×1-6,
累加,得bn-b1=2(1+2+…+n-1)-6(n-1)=n(n-1)-6n+6=n2-7n+6.
又∵b1=a2-a1=-14,∴bn=n2-7n-8(n≥2),
当n=1时,b1也适合此式,故bn=n2-7n-8(n∈N*).
(2)由bn=(n-8)(n+1)得,an+1-an=(n-8)(n+1),
∴当n<8时,an+1<an;当n=8时,a9=a8;
当n>8时,an+1>an.
∴当n=8或n=9时,an的值最小.
18.解:(1)a16+a17+a18=a9=-18,∴a17=-6,又a9=-18,∴d==.
首项a1=a9-8d=-30,∴an=n-.
设前n项和为Sn最小,则,即,∴n=20或n=21.
这表明当n=20或21时,Sn取最小值,最小值为S20=S21=-315.
(2)由an=n-≤0⇒n≤21,∴当n≤21时,Tn=-Sn=(41n-n2),
当n>21时,Tn=-a1-a2-…-a21+a22+…+an=Sn-2S21=(n2-41n)+630.
19.解: (1)∵an+1=3an-2an-1(n≥2,n∈N*),∴(an+1-an)=2(an-an-1)(n≥2,n∈N*).
∵a1=2,a2=4,∴a2-a1=2≠0,∴an-an-1≠0(n≥2,n∈N*).
故数列{an+1-an}是首项为2,公比为2的等比数列,∴an+1-an=(a2-a1)2n-1=2n,
∴an=(an-an-1)+(an-1-an-2)+(an-2-an-3)+…+(a2-a1)+a1
=2n-1+2n-2+2n-3+…+21+2=+2=2n(n≥2,n∈N*).
又a1=2满足上式,∴an=2n(n∈N*).
(2)由(1)知bn==2=2=2-(n∈N*),
∴Sn=2n-=2n-=2n-2=2n-2+.
20.解:(1)依题意,Sn+1-Sn=an+1=Sn+3n,
即Sn+1=2Sn+3n,
∴Sn+1-3n+1=2(Sn-3n),即bn+1=2bn.
∴数列{bn}是首项b1=a-3,公比为2的等比数列.
∴所求通项公式为bn=Sn-3n=(a-3)2n-1,n∈N*①
(2)由①知Sn=3n+(a-3)2n-1,n∈N*,
于是,当n≥2时,
an=Sn-Sn-1=3n+(a-3)2n-1-3n-1-(a-3)2n-2=2×3n-1+(a-3)2n-2,
an+1-an=4×3n-1+(a-3)2n-2=2n-2×,
当n≥2时,∵an+1≥an,∴12×n-2+a-3≥0,∴a≥-9.
又a2=a1+3>a1,综上,所求a的取值范围是[-9,+∞).