
1.下列函数中,周期为π,且为偶函数的是 ( )
A. = | sin
= | sin | B.
| B. = 2sin
= 2sin .cos
.cos
C. = cos
= cos D.
D. =cos
=cos
2.已知全集U = Z ,A={1,3,5},B={  |
|  3
- 2
3
- 2 2 - 3
2 - 3 = 0},则B∩CuA等于( )
= 0},则B∩CuA等于( )
A.{1,3} B.{0,-1} C.{1,5} D.{0,1}
3.双曲线中心在原点,实轴长为2,它的一个焦点为抛物线 2 = 8
2 = 8 的焦点,则此双曲线方程为 (
)
的焦点,则此双曲线方程为 (
)
A. -
- 2 = 1 B.
2 = 1 B. -
- 2 = 1 C.
2 = 1 C. 2 -
2 - = 1 D.
= 1 D. 2-
2- = 1
= 1
4.设a.b为两条直线, .β为两个平面,则下列命题正确的是 (
)
.β为两个平面,则下列命题正确的是 (
)
A.a.b与 成等角,则a//b; B.若a∥
成等角,则a//b; B.若a∥ ,b∥β,
,b∥β, ∥β则a∥b;
∥β则a∥b;
C.a
 ,b
,b β,a∥b则
β,a∥b则 ∥β; D.a
∥β; D.a
 ,b
,b β,
β, ∥β则a∥b.
∥β则a∥b.
5.设a1 = 2,数列|1+2an|是以3为公比的等比数列,则a4的值为 ( )
A.67 B.77 C.22 D.202
6.已知向量 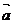 =(-1,2),
=(-1,2), =(2,1),则
=(2,1),则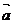 与
与 的位置关系是 (
)
的位置关系是 (
)
A.平行且同向 B.不垂直也不平行 C.垂直 D.平行且向反
7.随机变量 的分布列如下,其中a\b\c成等差数列,且E
的分布列如下,其中a\b\c成等差数列,且E =b,则a、b、c的值 分别为( )
=b,则a、b、c的值 分别为( )
 |
-1 |
0 |
1 |
|
p |
a |
b |
c |
A. ,
, ,
, B.
B. ,
, ,
, C.
C. ,
, ,
, D.
D. ,
, ,
,
8.若 (χ)= 3x的反函数为g(
(χ)= 3x的反函数为g( ),且g(a)+g(b)=2,则
),且g(a)+g(b)=2,则 +
+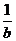 的最小值为 (
)
的最小值为 (
)
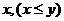 A.
A. B.
B. C.
C. D.1
D.1

9.定义运算
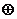 y
= 若|
m-2 |
y
= 若|
m-2 | 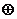 m = | m-2|,则m的取值范围是 ( )
m = | m-2|,则m的取值范围是 ( )
A.(- ,1) B.[1,+
,1) B.[1,+ ] C.(0,+
] C.(0,+ ) D.(-
) D.(- ,0)
,0)
|
 (
( ) =
) =  在
在 = 1处连续,则a的值为 (
)
= 1处连续,则a的值为 (
)
A.1 B.2 C.3 D.5
11.不等式log3( | – 5 | + |
– 5 | + | + 4
| ) > a对于
+ 4
| ) > a对于
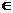 R恒成立,则a的取值范围是 (
)
R恒成立,则a的取值范围是 (
)
 A.(-
A.(- ,9) B.(-
,9) B.(- ,2) C.(2,9) D.[1,+
,2) C.(2,9) D.[1,+ ]
]
12.有n支球队参加单循环赛,其中两个队各赛了三场就退出了比赛,且此两队之间未进行比赛,这样到比赛结束时共赛了34场,那么n等于 ( )
A.12 B.11 C.10 D.9
|
13.某工厂生产A.B.C三种不同型号的产品,产品数量之比依次为3:4:7现用分层抽样方法取出一个容量为n的样本,样本中B型号产品有28件,那么此样本的容量n=
14.设实数 .
. 满足
满足 则
则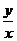 的最大值为
.
的最大值为
.
15.定义运算
 =
ad – bc,若复数
=
ad – bc,若复数 满足
满足
 =
=

则 .
.
16.点P在正方形ABCD所在的平面外,PD 平面ABCD,且PD=AD,则PA与BD所成角的大小为
.
平面ABCD,且PD=AD,则PA与BD所成角的大小为
.
17.(12分)某地一天从6时到14时的温度变化曲线如图示,它近似满足函数
 y=Asin(
y=Asin(
 +
+ )+b.
)+b.
(1)求这段时间的最大温差;
(2)试求这段曲线的函数解析式.
18.(12分)袋中有大小相同的5个白球和3个 黑球,现从中任意摸出4个,求下列事件发生的概率:
(1)摸出2个或3个白球;
(2)至少摸出一个黑球.
19.(12分)如图,在三棱锥P-ABC中,△ABC是边长为2的等边三角形,且∠PCA=∠PCB
(1)求证:PC AB;
AB;
(2)若O为△ABC的中心,G为△PAB的重心,求证:GO∥平面PAC;
 (3)若
(3)若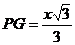 , 二面角
, 二面角 为锐角,求侧棱PC的取值范围.
为锐角,求侧棱PC的取值范围.
20.(12分)已知函数 (
( ) = a
) = a 3
+ b
3
+ b 2 + c(a,b,c∈R,a≠0)
的图像过点P( -1, 2 ),且在点P处的切线与直线
2 + c(a,b,c∈R,a≠0)
的图像过点P( -1, 2 ),且在点P处的切线与直线 - 3
- 3 = 0垂直.
= 0垂直.
(1)若c = 0试求函数 (
( )的单调区间;
)的单调区间;
(2)若 a > 0 , b > 0且 ( - , m ) , ( n ,+
, m ) , ( n ,+ )是
)是 (
( )的单调递增区间,试求n - m的范围.
)的单调递增区间,试求n - m的范围.
21.(12分)设椭圆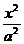 +
+ =
1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线
=
1( a > b > 0 )的左焦点为F,上顶点为A.过A做直线
 AF
AF
l分别交椭圆和 轴正半轴于P、Q两点,若
轴正半轴于P、Q两点,若 分AQ所成的比为8∶5.
分AQ所成的比为8∶5.
(1)求椭圆的离心率;
(2)若过A、Q、F三点的圆恰好与直线 +
+
 + 3 = 0相切,求椭圆方程.
+ 3 = 0相切,求椭圆方程.
22.(14分)
设函数g( )对任意的
)对任意的 、
、 ∈(0,+
∈(0,+ ),都有g(
),都有g( .
. )=g(
)=g( ) + g(
) + g( )成立,又g(2) = 1;已知点pn(an,bn)(n ∈ N* )都在直线
)成立,又g(2) = 1;已知点pn(an,bn)(n ∈ N* )都在直线 :
: = 2
= 2 +
2上,P1为直线
+
2上,P1为直线 与
与 轴的交点,数列{bn}满足n ≥ 2时,bn >0,且g(sn) = g(bn) + g(2+bn) - 2,(n ∈ N* ),其中Sn是数列{bn}的前n项和.
轴的交点,数列{bn}满足n ≥ 2时,bn >0,且g(sn) = g(bn) + g(2+bn) - 2,(n ∈ N* ),其中Sn是数列{bn}的前n项和.
(1)求数列{an}、{bn}的通项公式;
(2)若 (n) =
(n) = 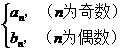 是否存在
是否存在 ∈N*,使得
∈N*,使得 (
( +5)=2
+5)=2 (
( )-2成立?
)-2成立?
若 存在,求出
存在,求出 值;若不存在,说明理由;
值;若不存在,说明理由;
(3)求证: +
+ 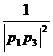 + … +
+ … +  <
<  .(n ≥ 2,n ∈ N* )
.(n ≥ 2,n ∈ N* )
08年宝鸡市高考理科数学教学质量检测(一) 数学(理科)试题 本试卷分第I卷(选择题)和第II卷(非选择题)两部分。考试时间120分钟。 第I卷(选择题,共60分) ●以下公式供解题时参考: 如果事件A、B互斥,那么P(A+B)=P (A)+P(B);如果事件A、B相互独立,那么 P(A.B)=P(A).P(B); 如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中参考答案
参考答案
选择题(本大题共12小题,每小题5分,共60分)
|
题号 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
||
|
答案 |
A |
B |
D |
D |
A |
C |
A |
B |
B |
D |
B |
|
13.98 14. 15.(理)-2±
15.(理)-2±

 (文)(
(文)( -1)2 + 4
-1)2 + 4 2 =
1 16.
2 =
1 16.
三、解答题
17.解:(1)由图示,这段时间的最大温差是30-10=20( )…………………………4′
)…………………………4′
(2)图中从6时到14时的图像是函数 =Asin(
=Asin(
 +
+ )+b的半个周期的图像.
)+b的半个周期的图像.
∴ .
. = 14-6,解得
= 14-6,解得 =
=  …………………………………………………………6′
…………………………………………………………6′
由图示A =  (30 - 10)=
10,b =
(30 - 10)=
10,b =  (30+10)
= 20,这时
(30+10)
= 20,这时 =10sin(
=10sin(
 +
+  )+ 20…
)+ 20…
………………………………………………………………………………………………8′
将 = 6,
= 6,  =
10代入上式可取
=
10代入上式可取 =
=
 ,…………………………………………… 10′
,…………………………………………… 10′
综上所求的解析式为 =10sin(
=10sin(
 +
+ 
 )+
20,
)+
20, ∈[6,14].
………………………12′
∈[6,14].
………………………12′
18.解:(1)设摸出的4个球中有2个白球、3个白球分别为事件A、B,
则P(A)=
 =
=  ,P(B)=
,P(B)=
 =
=  .……………………………4′
.……………………………4′
∵A、B为两个互斥时间,∴P(A+B)= P(A)+P(B)=
 .
.
即摸出的4个球中有2个或3个白球的概率为 ………………………………………6′
………………………………………6′
(2)设摸出的4个球中全是白球为事件C,则P(C)=  =
=  ,……………10′
,……………10′
“至少摸出一个黑球”为事件C的对立事件,其概率为P = 1- =
=  . ………12′
. ………12′
19.证明:(1)设H为AB中点,连PH、CH.……………………………………………2′
∠PCA=
 △PCA
△PCA △PCB
△PCB
|
在等边三角形ABC中,
 平面PCH
平面PCH ……
……
………………………………………………………………………………理8′(文12′)
(2)点G.O分别在PH.CH上, 平面PAC
平面PAC
(理)(3)由(1)可知∠PHC= 为二面角P – AB – C的平面角,
为二面角P – AB – C的平面角, 为锐角,cos
为锐角,cos > 0.
> 0.
在等边三角形ABC中,CH= ,PG=
,PG=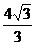
 PH
=
PH
=  PG=2
PG=2 ,
,
设PC
= ,则
,则 2 = 3 + 12 - 12 cos
2 = 3 + 12 - 12 cos
 cos
cos =
=  >
0,
>
0,
 即
即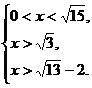

 <
<
 <
<  .……………12′
.……………12′
20.解:(1)由 (
( )过点P得-a
+ b + c = 2,
)过点P得-a
+ b + c = 2,  ˊ(
ˊ( )=3a
)=3a 2 + 2b
2 + 2b , ………………2′
, ………………2′
因为 (
( )在P处的切线与
)在P处的切线与 - 3
- 3 =
0垂直,所以3a –
2b = -3.
=
0垂直,所以3a –
2b = -3.
又c
= 0,解得a = 1,b = 3,所以 ′(
′( )=3
)=3 2
+ 6
2
+ 6 .………………………………4′
.………………………………4′
令 ˊ(
ˊ( ) = 0得
) = 0得 1 = 0,
1 = 0,  2 = -2;
2 = -2;
当x>0或 < -2,
< -2, ˊ(
ˊ( ) > 0,当 –2 <
) > 0,当 –2 < < 0 ,
< 0 , ˊ(
ˊ( ) < 0,
) < 0,
所以(- ,-2),(0,+
,-2),(0,+ )是f(
)是f( )的单调递增区间,(-2,0)是
)的单调递增区间,(-2,0)是 (
( )的单调递减区间.
)的单调递减区间.
…………………………………………………………………………………………… 6′
(2)由 ′(
′( ) = 3a
) = 3a 2 + 2b
2 + 2b =0,得
=0,得 1=0,
1=0,  2 = -
2 = - .……………………………… 8′
.……………………………… 8′
又因为a > 0,b > 0所以当 > 0,或χ<
> 0,或χ<  ,
, ˊ(
ˊ( ) > O,
) > O,
因此(- ,-
,- ),(
0,+
),(
0,+ )是
)是 (
( )的单调递增区间,……………………………10′
)的单调递增区间,……………………………10′
于是有n – m = 0 -(- ) =
) =  .由(1)知-a + b + c = 2,且3a
- 2b = -3,
.由(1)知-a + b + c = 2,且3a
- 2b = -3,
所以a
= 1 - 2c > 0,b = 3 - 3c > 0,从而得c < .
.
n– m =  =
=
 .
. = 1 -
= 1 -  >
1,故n – m >1.……………………12′
>
1,故n – m >1.……………………12′
21.解:(1)由F(-c,0),A(0,b)知直线AP方程为 – b = -
– b = - 
 ,令
,令 = 0得
= 0得
|
 ,0)………………………………………………………………………………2′
,0)………………………………………………………………………………2′
设P( 0,
0,  0),P分AQ所成的比为
0),P分AQ所成的比为 =
=  ,
,

|
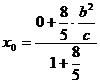

代入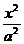 +
+  =
1 中得2b2 = 3ac,又b2
= a2-c2,解得离心率c =
=
1 中得2b2 = 3ac,又b2
= a2-c2,解得离心率c = .………………6′
.………………6′
(2)Rt△AOF中,|
AF | = a,sin∠FAO =  =
=  ∠FAO =
∠FAO =  ,∠AQF =
,∠AQF =  ,
,
则| FQ | = 2| AF |= 2a = 4c,故圆心B(c,0),
∴Rt△QAF的外接圆方程为( – c )2 +
– c )2 +  2 = a2,……………………………………10′
2 = a2,……………………………………10′
该圆与 +
+
 + 3 = 0相切,则d =
+ 3 = 0相切,则d =  = a .
= a .
即c
+ 3 = 2a = 2×2c c = 1,则a =2,b2
= 3.
c = 1,则a =2,b2
= 3.
∴所求椭圆方程为 +
+ =
1.……………………………………………………12′
=
1.……………………………………………………12′
22.解(1)(理)P1(a1,b1)为直线 = 2χ+ 2与
= 2χ+ 2与 轴交点,则a1 = -1,b1 = 0………2′
轴交点,则a1 = -1,b1 = 0………2′
由已知 、
、 ∈(0,+
∈(0,+ ),都有g(x.
),都有g(x. ) = g(
) = g( ) +
g(
) +
g( )成立,又g(2) = 1,
)成立,又g(2) = 1,
得g(4)
= =g(2 2) = g(2) + g(2) = 2,
2) = g(2) + g(2) = 2,
因为n ≥ 2时,bn > 0,且g(Sn) = g(bn) + g(2+bn) - 2,( n∈N* )
所以2 + g( Sn ) = g( bn ) + g( 2+bn ),即g(4) +g( Sn ) = g( bn ) + g( 2+bn ).
所以4Sn = bn(2+bn) b2 = 2, b2 – b1
= 2;
b2 = 2, b2 – b1
= 2;
由4Sn = bn
(2+bn)及4Sn+1 = bn+1(2 + bn+1) bn+1 - bn = 2
bn+1 - bn = 2
所以{bn}是以0为首项,2为公差的等差数列,∴bn = 2n-2 ………………………4′
因为Pn(
an,bn)( n ∈ N )在直线y = 2
)在直线y = 2 + 2上,
+ 2上,
则bn = 2an + 2,∴an = n - 2.………………………………………………………………6′
(1)(文)解:P1=(a1,b1)为直线 = 2
= 2 +
2与
+
2与 轴交点,则a1 = -1,b1 =
0 ……2′
轴交点,则a1 = -1,b1 =
0 ……2′
∴an
= -1 + ( n – 1 ) = n – 2, (n∈N*)在直线
(n∈N*)在直线 = 2
= 2 + 2上,
+ 2上,
则bn = 2an + 2,∴bn = 2n - 2.…………………………………………………………4′
(2) 为偶数时,
为偶数时, (
( + 5) = ak+ 5
=
+ 5) = ak+ 5
= + 3,2
+ 3,2  (
( ) – 2 = 2( 2
) – 2 = 2( 2 –
2 ) – 2 = 4
–
2 ) – 2 = 4 - 6
- 6
由 + 3 = 4
+ 3 = 4 - 6
- 6
 = 3
,与
= 3
,与 为偶数矛盾,
为偶数矛盾,
 为奇数时,
为奇数时, (
( +5) = bk+5 = 2
+5) = bk+5 = 2 + 8,2 ƒ (
+ 8,2 ƒ ( ) – 2 = 2
) – 2 = 2 - 6
- 6
由2 + 8 = 2
+ 8 = 2 - 6得
- 6得 不存在.故满足条件的
不存在.故满足条件的 不存在.…………………理10′(文9′)
不存在.…………………理10′(文9′)
(3)| P1Pn |2 =( n – 1 )2 + ( 2n – 2 )2 = 5( n – 1 )2,n ≥ 2,
 +
+  + … +
+ … + 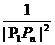 =
=  [
[ +
+ +
… +
+
… +  ]
]
≤ [
[ +
+
 … +
… +  ]
]
= 
∴ …
+
…
+  ………………………14′
………………………14′