
四川省双流县2009届高三第二次诊断性模拟考试
文科数学
考生注意;全卷满分150分,完成时间120分钟
第I卷(选择题共60分)
一、选择题:(本题只有12个题,每小题5分,共60分)在每小题给出的四个选项中,只有一个正确,把正确选项的代号填在机读卡的指定位置上。
1.已知A,B满足运算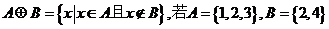 ,则
,则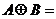
A.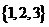 B.
B.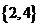 C.
C. 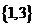 D.
D.
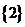
2.不等式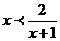 的解集是
的解集是
A.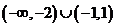 B.
B.
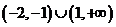
C. 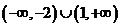 D.
D.
3.若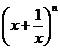 展开式的二项式系数之和为64,则展开式的常数项为
展开式的二项式系数之和为64,则展开式的常数项为
A.10 B.
4.若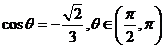 ,则
,则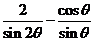 的值是
的值是
A.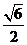 B.
B.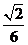 C.
C.
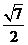 D.
D.
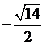
5.设等差数列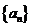 的公差
的公差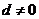 ,且
,且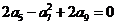 ,数列
,数列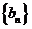 是等比数列,且
是等比数列,且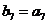 ,则
,则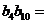
A.2 B.
6.在坐标平面上,横坐标与纵坐标均为整数的点称为整点,对任意自然数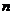 ,连结原点
,连结原点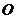 与点
与点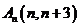 ,用
,用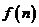 表示线段
表示线段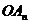 上除端点外的整点个数,则
上除端点外的整点个数,则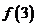
A.1 B.
7.函数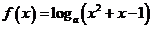 在区间上
在区间上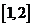 的最大值比最小值大2,则实数
的最大值比最小值大2,则实数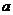 的值为
的值为
A.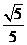 B.
B.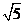 C.
C.
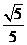 或
或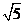 D.不能确定
D.不能确定
8.用1、2、3、4四个数字构造一个四位数,这个数个位数字是1,且恰好有两个相同数字的概率是
A. B.
B.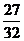 C.
C.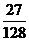 D.
D.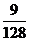
9.已知棱锥的顶点为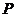 ,
,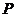 在底面上的射影为
在底面上的射影为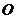 ,
,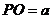 现用平行于底面的平面去截这个棱锥,截面交
现用平行于底面的平面去截这个棱锥,截面交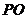 于点
于点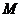 ,并使截得的两部分侧面积相等,设
,并使截得的两部分侧面积相等,设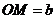 ,则
,则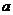 与
与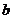 的关系是
的关系是
A.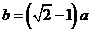 B.
B.
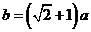
C. 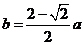 D.
D.
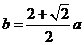
10. 已知平面上两点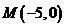 和
和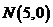 ,若直线上存在点P使
,若直线上存在点P使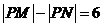 ,则称该直线为“单曲型直线”,下列直线中是“单曲型直线”的是
,则称该直线为“单曲型直线”,下列直线中是“单曲型直线”的是
①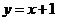 ②
②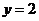 ③
③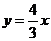 ④
④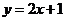
A.①③ B. ③④ C. ②③ D. ①②
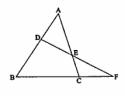 11.如图直线
11.如图直线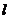 与
与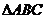 的三边交于
的三边交于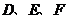 三点,若
三点,若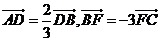 ,则
,则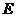 点分
点分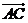 所成的比是
所成的比是
A.2 B.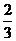 C.
C.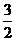 D.3
D.3
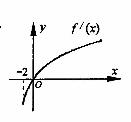 12.已知
12.已知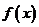 函数的定义域为
函数的定义域为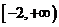 ,且
,且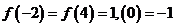 ,设
,设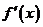 为
为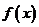 的导函数,函数
的导函数,函数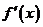 的图像如图所示,若两正数
的图像如图所示,若两正数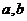 满足
满足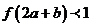 ,则
,则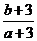 的取值范围是
的取值范围是
A.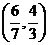 B.
B.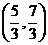
C.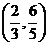 D.
D.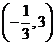
第II卷(非选择题共90分)
二、填空题(本大题共4小题,共16分)把答案填在题中横线上。
13.10名同学合影,站成了前排3人后排7人,现摄影师要从后排7人中抽2人站到前排,其他人的相对顺序不变,则不同调整方法的种数为
14.已知圆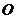 的半径为
的半径为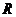 ,它的内接
,它的内接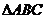 满足
满足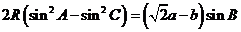 ,则
,则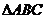 面积的最大值是
面积的最大值是
15.已知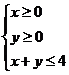 所确定的平面区域记为D.若圆
所确定的平面区域记为D.若圆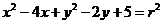 所有的点都在区域D上,则圆的面积的最大值为
所有的点都在区域D上,则圆的面积的最大值为
16.给出如下4个命题:①若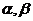 是两个不重合的平面,
是两个不重合的平面,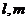 是两条不重合的直线,则
是两条不重合的直线,则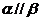 的一个充分而不必要条件是
的一个充分而不必要条件是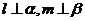 ,且
,且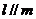 ;②对于任意一条直线
;②对于任意一条直线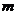 ,平面
,平面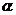 内必有无数条直线与
内必有无数条直线与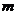 垂直;③已知命题
垂直;③已知命题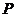 :“若四点不共面,那么这四点中任何三点都不共线。”则命题
:“若四点不共面,那么这四点中任何三点都不共线。”则命题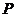 的逆否命题是假命题;④已知
的逆否命题是假命题;④已知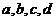 是四条不重合的直线,如果
是四条不重合的直线,如果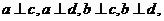 ,则“
,则“ ”与“
”与“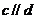 ”不可能都不成立。在以上4个命题中,正确命题的序号是
”不可能都不成立。在以上4个命题中,正确命题的序号是
(要求将所有你认为正确的命题序号都填上)
三、解答题(本大题共6个小题,共74分)
17.(本大题满分12分)
已知函数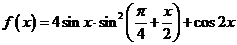
(1)
若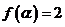 ,且
,且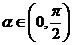 ,求
,求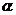 的值;
的值;
(2)设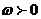 为常数,若
为常数,若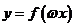 在区间
在区间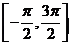 上是增函数,求
上是增函数,求 的取值范围。
的取值范围。
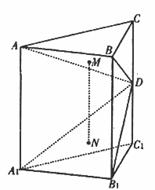
18. (本大题满分12分)
如图,直三棱柱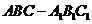 中,
中,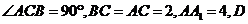 为棱
为棱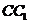 上的一动点,
上的一动点,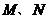 分别为
分别为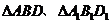 的重心。
的重心。
(1)求证: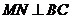
(2)若点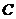 在
在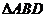 上的正射影正好为
上的正射影正好为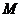
求二面角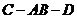 的大小;
的大小;
19. (本大题满分12分)
在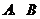 两只口袋中均放有2个红球和2个白球,先
两只口袋中均放有2个红球和2个白球,先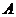 从袋中任取2个球放到
从袋中任取2个球放到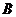 袋中,再从
袋中,再从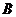 袋中任取一个球放到
袋中任取一个球放到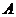 袋中,经过这样的操作之后。
袋中,经过这样的操作之后。
(1)求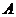 袋中没有红球的概率;
袋中没有红球的概率;
(2)求 袋中恰有一只红球的概率。
袋中恰有一只红球的概率。
20. (本大题满分12分)
已知数列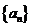 满足
满足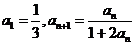
(1)证明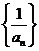 成等差数列,并求数列
成等差数列,并求数列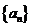 的通项公式
的通项公式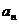 ;
;
(2)记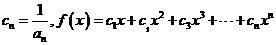 ,求证:
,求证: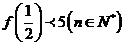
21. (本大题满分12分)
直线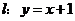 与椭圆
与椭圆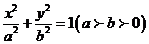 相交于
相交于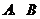 两个不同的点,与
两个不同的点,与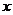 轴相交于点
轴相交于点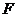 。
。
(1)证明: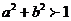 ;
;
(2)若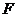 是椭圆的一个焦点,且
是椭圆的一个焦点,且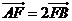 ,求椭圆的方程。
,求椭圆的方程。
22.(本题满分14分)
已知函数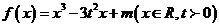 是奇函数。
是奇函数。
(1)试求函数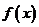 的单调区间;
的单调区间;
(2)若对任意的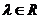 ,都存在
,都存在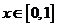 ,使得
,使得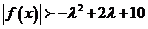 成立,求实数
成立,求实数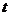 的取值范围。
的取值范围。
www.1010jiajiao.com
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com