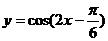广东省汕头市部分重点中学2009届高三毕业考试高考模拟数学(理)试题
考生注意:
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。满分150分,考试时间120分钟。考试结束后将第Ⅱ卷和答题卡一并交回。
第Ⅰ卷(选择题 共60分)
注意事项:
1.答第Ⅰ卷前,考生务必将自己的姓名、准考证号、考试科目、试卷类型用2B铅笔涂写在答题卡上。
2.每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净扫,再选涂其他答案,不能答在试题卷上。
一、选择题:本大题共12小题;每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.复数 (i是虚数单位)在复平面上对应的点位于 ( )
(i是虚数单位)在复平面上对应的点位于 ( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
试题详情
2.若集合 ”的 ( )
”的 ( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
试题详情
试题详情
试题详情
4.已知三条不重合的直线m、n、l两个不重合的平面 ,有下列命题
,有下列命题
试题详情
①若 ;
;
试题详情
②若 ;
;
试题详情
③若 ;
;
试题详情
④若 ;
;
其中正确的命题个数是 ( )
A.1 B.2 C.3 D.4
试题详情
5.由曲线 和直线x=1围成图形的面积是 ( )
和直线x=1围成图形的面积是 ( )
试题详情
试题详情
6.同时具有性质“①最小正周期是 ,②图象关于直线
,②图象关于直线 对称;③在
对称;③在 上是增
上是增
函数”的一个函数是 ( )
试题详情
A. B.
B.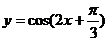
试题详情
C. D.
D.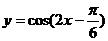
试题详情
|
试题详情
A. 的图象 B. 的图象 B. 的图象 的图象 试题详情
C. 的图象 D. 的图象 D. 的图象 的图象 试题详情
8.圆 关于直线 关于直线 对称,则ab的取值范 对称,则ab的取值范 围是 ( ) 试题详情
试题详情
|
试题详情
A. B. B.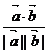 试题详情
C. D. D.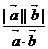
|
试题详情
试题详情
试题详情
A. B. B.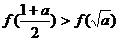 试题详情
C. D. D.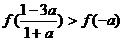 试题详情
12.如果一条直线与一个平面平行,那么称此直线与平面构成一个“平行线面组”,在一个长方体中,由两个顶点确定的直线与含有四个顶点的平面构成的“平行
线面组”的个数是 ( ) A.60 B.48 C.36 D.24
|
试题详情
二、填空题:本大题共4小题,每小题4分,共16分。把答案填在题中横线上。 13.某企业三月中旬生产,A、B、C三种产品共3000件,根据分层抽样的结果;企业统计员制作了如下的统计表格: 产品类别 A B C 产品数量(件) 1300 样本容量(件) 130 由于不小心,表格中A、C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10,根据以上信息,可得C的产品数量是
件。 试题详情
14.一个几何体的三视图如图所示,则该几何体外接球的表面积为
。 试题详情
|
试题详情
试题详情
试题详情
试题详情
①命题“ ”的否定是“ ”的否定是“ ”; ”; ②线性相关系数r的绝对值越接近于1,表明两个随机变量线性相关性越强; 试题详情
试题详情
④函数 上恒为正,则实数a的取值范围是 上恒为正,则实数a的取值范围是 。 。 其中真命题的序号是
。(填上所有真命题的序号) 试题详情
三、解答题:本大题共6小题,共计74分,解答应写出文字说明、证明过程或推演步骤。
试题详情
试题详情
(Ⅰ)求 的取值范围; 的取值范围; 试题详情
(Ⅱ)求 的最小值。 的最小值。 试题详情
18.(本小题满分12分) 一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球,取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分。
(Ⅰ)若从袋子里一次随机取出3个球,求得4分的概率; 试题详情
(Ⅱ)若从袋子里每次摸出一个球,看清颜色后放回,连续摸3次,求得分 的概率分布列及数学期望。 的概率分布列及数学期望。 试题详情
19.(本小题满分12分) 如图,棱柱ABCD―A1B1C1D1的所有棱长都等于2,∠ABC=60°,平面AA1C1C⊥平面ABCD,∠A1AC=60°。
(Ⅰ)证明:BD⊥AA1;
(Ⅱ)求二面角D―A1A―C的平面角的余弦值; 试题详情
|
试题详情
试题详情
已知函数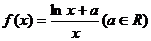 试题详情
(Ⅰ)求 的极值; 的极值; 试题详情
(Ⅱ)若函数 的图象与函数 的图象与函数 =1的图象在区间 =1的图象在区间 上有公共点,求实数a的取值范围。 上有公共点,求实数a的取值范围。 试题详情
21.(本小题满分12分) 如图,O是坐标原点,已知三 点E(0,3),F(0,1),G(0,-1),直线L:y=-1,M是直线L上的动点,H、P是坐标平面上的动点,且 试题详情
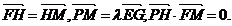
(Ⅰ)求动点P的轨迹方程; 试题详情
|
试题详情
试题详情
对 所表示的平面区域为Dn,Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列。 所表示的平面区域为Dn,Dn内的整点(横坐标与纵坐标均为整数的点)按其到原点的距离从近到远排成点列。 试题详情
试题详情
(Ⅰ)求 ; ; 试题详情
试题详情
(Ⅲ)在(Ⅱ)的条件下,试比较 与4的大小关系。 与4的大小关系。 试题详情
一、选择题(每小题5分,共12小题,满分60分)
2,4,6 二、填空题(每小题4分,共4小题,满分16分) 13.800 14. 15.625 16.②④ 15.625 16.②④ 三、解答题(本大题共6小题,满分74分) 17.解
(Ⅰ)由题意知 

……………………3分 
 ……………………4分 ……………………4分
 的夹角 的夹角

 ……………………6分 ……………………6分
(Ⅱ)  ……………………9分 ……………………9分


 有最小值。 有最小值。
 的最小值是 的最小值是 ……………………12分 ……………………12分
18.解: (Ⅰ)设“一次取出3个球得4分”的事件记为A,它表示取出的球中有1个红球和2个黑球的情况 则 ……………………4分 ……………………4分 (Ⅱ)由题意, 的可能取值为3、4、5、6。因为是有放回地取球,所以每次取到红球的概率为 的可能取值为3、4、5、6。因为是有放回地取球,所以每次取到红球的概率为 ……………………6分 ……………………6分 



 的分布列为 的分布列为

3 4 5 6 P 



……………………10分

19.解: 连接BD交AC于O,则BD⊥AC, 连接A1O 在△AA1O中,AA1=2,AO=1, ∠A1AO=60° ∴A1O2=AA12+AO2-2AA1?Aocos60°=3 ∴AO2+A1O2=A12 ∴A1O⊥AO,由于平面AA1C1C⊥ 平面ABCD, 所以A1O⊥底面ABCD ∴以OB、OC、OA1所在直线为x轴、y轴、z轴建立如图所示空间直角坐标系,则A(0,-1,0),B( ,0,0),C(0,1,0),D(- ,0,0),C(0,1,0),D(- ,0,0),A1(0,0, ,0,0),A1(0,0, ) ) ……………………2分 (Ⅰ)由于 
则 ∴BD⊥AA1……………………4分 (Ⅱ)由于OB⊥平面AA1C1C ∴平面AA1C1C的法向量 设 ⊥平面AA1D ⊥平面AA1D 则 得到 ……………………6分 ……………………6分 
所以二面角D―A1A―C的平面角的余弦值是 ……………………8分 ……………………8分 (Ⅲ)假设在直线CC1上存在点P,使BP//平面DA1C1 设 则 得 ……………………9分 ……………………9分 设 则 设 设 得到 ……………………10分 ……………………10分 又因为 平面DA1C1 平面DA1C1 则 ? ? 即点P在C1C的延长线上且使C1C=CP……………………12分 法二:在A1作A1O⊥AC于点O,由于平面AA1C1C⊥平面 ABCD,由面面垂直的性质定理知,A1O⊥平面ABCD, 又底面为菱形,所以AC⊥BD

……………………4分 (Ⅱ)在△AA1O中,A1A=2,∠A1AO=60° ∴AO=AA1?cos60°=1 所以O是AC的中点,由于底面ABCD为菱形,所以 O也是BD中点 由(Ⅰ)可知DO⊥平面AA1C 过O作OE⊥AA1于E点,连接OE,则AA1⊥DE 则∠DEO为二面角D―AA1―C的平面角 ……………………6分 在菱形ABCD中,AB=2,∠ABC=60° ∴AC=AB=BC=2 ∴AO=1,DO= 在Rt△AEO中,OE=OA?sin∠EAO= DE= ∴cos∠DEO= ∴二面角D―A1A―C的平面角的余弦值是 ……………………8分 ……………………8分 (Ⅲ)存在这样的点P 连接B1C,因为A1B1 AB AB DC DC ∴四边形A1B1CD为平行四边形。 ∴A1D//B1C 在C1C的延长线上取点P,使C1C=CP,连接BP……………………10分 因B1B CC1,……………………12分 CC1,……………………12分 ∴BB1 CP CP ∴四边形BB1CP为平行四边形 则BP//B1C ∴BP//A1D ∴BP//平面DA1C1 20.解: (Ⅰ) 令 ……………………2分 ……………………2分 当 是增函数 是增函数 当 是减函数……………………4分 是减函数……………………4分 ∴ ……………………6分 ……………………6分 (Ⅲ)(i)当 时, 时, ,由(Ⅰ)知 ,由(Ⅰ)知 上是增函数,在 上是增函数,在 上是减函数 上是减函数  ……………………7分 ……………………7分
又当 时, 时, 所以 所以 的图象在 的图象在 上有公共点,等价于 上有公共点,等价于 …………8分 …………8分 解得 …………………9分 …………………9分 (ii)当 时, 时, 上是增函数, 上是增函数, ∴ 所以原问题等价于 又 ∴无解………………11分
| | | | | | | | | | | | | | | | | | | |

 (i是虚数单位)在复平面上对应的点位于 ( )
(i是虚数单位)在复平面上对应的点位于 ( ) ”的 ( )
”的 ( ) 的展开式中含
的展开式中含 项的系数,则数列
项的系数,则数列 的前n项和为 ( )
的前n项和为 ( ) B.
B. C.
C. D.
D.
 ,有下列命题
,有下列命题 ;
; ;
; ;
; ;
; 和直线x=1围成图形的面积是 ( )
和直线x=1围成图形的面积是 ( )  C.
C. D.
D.
 ,②图象关于直线
,②图象关于直线 对称;③在
对称;③在 上是增
上是增 B.
B.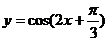
 D.
D.