
2009年高考数学难点突破专题辅导十四
难点14 数列综合应用问题
纵观近几年的高考,在解答题中,有关数列的试题出现的频率较高,不仅可与函数、方程、不等式、复数相联系,而且还与三角、立体几何密切相关;数列作为特殊的函数,在实际问题中有着广泛的应用,如增长率,减薄率,银行信贷,浓度匹配,养老保险,圆钢堆垒等问题.这就要求同学们除熟练运用有关概念式外,还要善于观察题设的特征,联想有关数学知识和方法,迅速确定解题的方向,以提高解数列题的速度.
●难点磁场
(★★★★★)已知二次函数y=f(x)在x= 处取得最小值-
处取得最小值- (t>0),f(1)=0.
(t>0),f(1)=0.
(1)求y=f(x)的表达式;
(2)若任意实数x都满足等式f(x)?g(x)+anx+bn=xn+1[g(x)]为多项式,n∈N*),试用t表示an和bn;
(3)设圆Cn的方程为(x-an)2+(y-bn)2=rn2,圆Cn与Cn+1外切(n=1,2,3,…);{rn}是各项都是正数的等比数列,记Sn为前n个圆的面积之和,求rn、Sn.
●案例探究
[例1]从社会效益和经济效益出发,某地投入资金进行生态环境建设,并以此发展旅游产业,根据规划,本年度投入800万元,以后每年投入将比上年减少 ,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加
,本年度当地旅游业收入估计为400万元,由于该项建设对旅游业的促进作用,预计今后的旅游业收入每年会比上年增加 .
.
(1)设n年内(本年度为第一年)总投入为an万元,旅游业总收入为bn万元,写出an,bn的表达式;
(2)至少经过几年,旅游业的总收入才能超过总投入?
命题意图:本题主要考查建立函数关系式、数列求和、不等式等基础知识;考查综合运用数学知识解决实际问题的能力,本题有很强的区分度,属于应用题型,正是近几年高考的热点和重点题型,属★★★★★级题目.
知识依托:本题以函数思想为指导,以数列知识为工具,涉及函数建模、数列求和、不等式的解法等知识点.
错解分析:(1)问an、bn实际上是两个数列的前n项和,易与“通项”混淆;(2)问是既解一元二次不等式又解指数不等式,易出现偏差.
技巧与方法:正确审题、深刻挖掘数量关系,建立数量模型是本题的灵魂,(2)问中指数不等式采用了换元法,是解不等式常用的技巧.
解:(1)第1年投入为800万元,第2年投入为800×(1- )万元,…第n年投入为800×(1-
)万元,…第n年投入为800×(1- )n-1万元,所以,n年内的总投入为
)n-1万元,所以,n年内的总投入为
an=800+800×(1- )+…+800×(1-
)+…+800×(1- )n-1=
)n-1= 800×(1-
800×(1- )k-1
)k-1
第1年旅游业收入为400万元,第2年旅游业收入为400×(1+ ),…,第n年旅游业收入400×(1+
),…,第n年旅游业收入400×(1+ )n-1万元.所以,n年内的旅游业总收入为
)n-1万元.所以,n年内的旅游业总收入为
bn=400+400×(1+ )+…+400×(1+
)+…+400×(1+ )k-1=
)k-1= 400×(
400×( )k-1.
)k-1.
(2)设至少经过n年旅游业的总收入才能超过总投入,由此bn-an>0,即:
1600×[( )n-1]-4000×[1-(
)n-1]-4000×[1-( )n]>0,令x=(
)n]>0,令x=( )n,代入上式得:5x2-7x+2>0.解此不等式,得x<
)n,代入上式得:5x2-7x+2>0.解此不等式,得x< ,或x>1(舍去).即(
,或x>1(舍去).即( )n<
)n< ,由此得n≥5.
,由此得n≥5.
∴至少经过5年,旅游业的总收入才能超过总投入.
[例2]已知Sn=1+ +…+
+…+ ,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2-
,(n∈N*)设f(n)=S2n+1-Sn+1,试确定实数m的取值范围,使得对于一切大于1的自然数n,不等式:f(n)>[logm(m-1)]2- [log(m-1)m]2恒成立.
[log(m-1)m]2恒成立.
命题意图:本题主要考查应用函数思想解决不等式、数列等问题,需较强的综合分析问题、解决问题的能力.属★★★★★级题目.
知识依托:本题把函数、不等式恒成立等问题组合在一起,构思巧妙.
错解分析:本题学生很容易求f(n)的和,但由于无法求和,故对不等式难以处理.
技巧与方法:解决本题的关键是把f(n)(n∈N*)看作是n的函数,此时不等式的恒成立就转化为:函数f(n)的最小值大于[logm(m-1)]2- [log(m-1)m]2.
[log(m-1)m]2.
∴f(n+1)>f(n)
∴f(n)是关于n的增函数
∴要使一切大于1的自然数n,不等式
f(n)>[logm(m-1)]2- [log(m-1)m]2恒成立
[log(m-1)m]2恒成立
只要 >[logm(m-1)]2-
>[logm(m-1)]2- [log(m-1)m]2成立即可
[log(m-1)m]2成立即可
此时设[logm(m-1)]2=t 则t>0
由此得0<[logm(m-1)]2<1
●锦囊妙计
1.解答数列综合题和应用性问题既要有坚实的基础知识,又要有良好的思维能力和分析、解决问题的能力;解答应用性问题,应充分运用观察、归纳、猜想的手段,建立出有关等差(比)数列、递推数列模型,再综合其他相关知识来解决问题.
2.纵观近几年高考应用题看,解决一个应用题,重点过三关:
(1)事理关:需要读懂题意,明确问题的实际背景,即需要一定的阅读能力.
(2)文理关:需将实际问题的文字语言转化数学的符号语言,用数学式子表达数学关系.
(3)事理关:在构建数学模型的过程中;要求考生对数学知识的检索能力,认定或构建相应的数学模型,完成用实际问题向数学问题的转化.构建出数学模型后,要正确得到问题的解,还需要比较扎实的基础知识和较强的数理能力.
●歼灭难点训练
一、选择题
1.(★★★★★)已知二次函数y=a(a+1)x2-(2a+1)x+1,当a=1,2,…,n,…时,其抛物线在x轴上截得的线段长依次为d1,d2,…,dn,…,则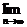 (d1+d2+…+dn)的值是( )
(d1+d2+…+dn)的值是( )
A.1 B.2 C.3 D.4
二、填空题
2.(★★★★★)在直角坐标系中,O是坐标原点,P1(x1,y1)、P2(x2,y2)是第一象限的两个点,若1,x1,x2,4依次成等差数列,而1,y1,y2,8依次成等比数列,则△OP1P2的面积是_________.
3.(★★★★)从盛满a升酒精的容器里倒出b升,然后再用水加满,再倒出b升,再用水加满;这样倒了n次,则容器中有纯酒精_________升.
4.(★★★★★)据
三、解答题
5.(★★★★★)已知数列{an}满足条件:a1=1,a2=r(r>0),且{anan+1}是公比为q(q>0)的等比数列,设bn=a2n-1+a2n(n=1,2,…).
(1)求出使不等式anan+1+an+1an+2>an+2an+3(n∈N*)成立的q的取值范围;
6.(★★★★★)某公司全年的利润为b元,其中一部分作为奖金发给n位职工,奖金分配方案如下:首先将职工按工作业绩(工作业绩均不相同)从大到小,由1到n排序,第1位职工得奖金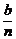 元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
元,然后再将余额除以n发给第2位职工,按此方法将奖金逐一发给每位职工,并将最后剩余部分作为公司发展基金.
(1)设ak(1≤k≤n)为第k位职工所得奖金金额,试求a2,a3,并用k、n和b表示ak(不必证明);
(2)证明ak>ak+1(k=1,2,…,n-1),并解释此不等式关于分配原则的实际意义;
7.(★★★★)据有关资料,1995年我国工业废弃垃圾达到7.4×108吨,占地562.4平方公里,若环保部门每年回收或处理1吨旧物资,则相当于处理和减少4吨工业废弃垃圾,并可节约开采各种矿石20吨,设环保部门1996年回收10万吨废旧物资,计划以后每年递增20%的回收量,试问:
(1)2001年回收废旧物资多少吨?
(2)从1996年至2001年可节约开采矿石多少吨(精确到万吨)?
(3)从1996年至2001年可节约多少平方公里土地?
8.(★★★★★)已知点的序列An(xn,0),n∈N,其中x1=0,x2=a(a>0),A3是线段A1A2的中点,A4是线段A2A3的中点,…,An是线段An-2An-1的中点,….
(1)写出xn与xn-1、xn-2之间关系式(n≥3);
(2)设an=xn+1-xn,计算a1,a2,a3,由此推测数列{an}的通项公式,并加以证明;
难点磁场
解:(1)设f(x)=a(x- )2-
)2- ,由f(1)=0得a=1.
,由f(1)=0得a=1.
∴f(x)=x2-(t+2)x+t+1.
(2)将f(x)=(x-1)[x-(t+1)]代入已知得:
(x-1)[x-(t+1)]g(x)+anx+bn=xn+1,上式对任意的x∈R都成立,取x=1和x=t+1分别代入上式得:
 且t≠0,解得an=
且t≠0,解得an= [(t+1)n+1-1],bn=
[(t+1)n+1-1],bn= [1-(t+1
[1-(t+1 n)
n)
(3)由于圆的方程为(x-an)2+(y-bn)2=rn2,又由(2)知an+bn=1,故圆Cn的圆心On在直线x+y=1上,又圆Cn与圆Cn+1相切,故有rn+rn+1= |an+1-an|=
|an+1-an|= (t+1)n+1?
(t+1)n+1?
∴Sn=π(r12+r22+…+rn2)= [(t+1)2n-1]
[(t+1)2n-1]
歼灭难点训练
一、1.解析:当a=n时y=n(n+1)x2-(2n+1)x+1
答案:A
二、2.解析:由1,x1,x2,4依次成等差数列得:2x1=x2+1,x1+x2=5解得x1=2,x2=3.又由1,y1,y2,8依次成等比数列,得y12=y2,y1y2=8,解得y1=2,y2=4,
答案:1
3.解析:第一次容器中有纯酒精a-b即a(1- )升,第二次有纯酒精a(1-
)升,第二次有纯酒精a(1- )-
)- ,即a(1-
,即a(1- )2升,故第n次有纯酒精a(1-
)2升,故第n次有纯酒精a(1- )n升.
)n升.
4.解析:从2001年到2005年每年的国内生产总值构成以95933为首项,以7.3%为公比的等比数列,∴a5=95933(1+7.3%)4≈120000(亿元).
答案:120000
三、
5.解:(1)由题意得rqn-1+rqn>rqn+1.由题设r>0,q>0,故从上式可得:q2-q-1<0,解得 <q<
<q< ,因q>0,故0<q<
,因q>0,故0<q< ;
;
(2)∵ .b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列,从而bn=(1+r)qn-1.
.b1=1+r≠0,所以{bn}是首项为1+r,公比为q的等比数列,从而bn=(1+r)qn-1.
当q=1时,Sn=n(1+r),
 ,从上式可知,当n-20.2>0,即n≥21(n∈N*)时,Cn随n的增大而减小,故
,从上式可知,当n-20.2>0,即n≥21(n∈N*)时,Cn随n的增大而减小,故
当n-20.2<0,即n≤20(n∈N*)时,Cn也随n的增大而减小,故1>Cn≥C20=1+ =-4 ②
=-4 ②
综合①②两式知,对任意的自然数n有C20≤Cn≤C21,故{Cn}的最大项C21=2.25,最小项C20=-4.
6.解:(1)第1位职工的奖金a1= ,第2位职工的奖金a2=
,第2位职工的奖金a2= (1-
(1- )b,第3位职工的奖金a3=
)b,第3位职工的奖金a3= (1-
(1- )2b,…,第k位职工的奖金ak=
)2b,…,第k位职工的奖金ak= (1-
(1- )k-1b;
)k-1b;
(2)ak-ak+1= (1-
(1- )k-1b>0,此奖金分配方案体现了“按劳分配”或“不吃大锅饭”的原则.
)k-1b>0,此奖金分配方案体现了“按劳分配”或“不吃大锅饭”的原则.
(3)设fk(b)表示奖金发给第k位职工后所剩余数,则f1(b)=(1- )b,f2(b)=(1-
)b,f2(b)=(1- )2b,…,fk(b)=(1-
)2b,…,fk(b)=(1- )kb.得Pn(b)=fn(b)=(1-
)kb.得Pn(b)=fn(b)=(1- )nb,
)nb,
7.解:设an表示第n年的废旧物资回收量,Sn表示前n年废旧物资回收总量,则数列{an}是以10为首项,1+20%为公比的等比数列.
(1)a6=10(1+20%)5=10×1.25=24.8832≈25(万吨)
∴从1996年到2000年共节约开采矿石20×99.3≈1986(万吨)
(3)由于从1996年到2001年共减少工业废弃垃圾4×99.3=397.2(万吨),
∴从1996年到2001年共节约:
证法一:因为a1=a>0,且
证法二:用数学归纳法证明:
(?)当n=1时,a1=x2-x1=a=(- )0a,公式成立;
)0a,公式成立;
(?)假设当n=k时,公式成立,即ak=(- )k-1a成立.
)k-1a成立.
那么当n=k+1时,
据(?)(?)可知,对任意n∈N,公式an=(- )n-1a成立.
)n-1a成立.
(3)当n≥3时,有xn=(xn-xn-1)+(xn-1-xn-2)+…+(x2-x1)+x1
=an-1+an-2+…+a1,
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com