
2009届高考数学第三轮复习精编模拟四
参考公式:
如果事件 互斥,那么
球的表面积公式
互斥,那么
球的表面积公式


如果事件 相互独立,那么
其中
相互独立,那么
其中 表示球的半径
表示球的半径
 球的体积公式
球的体积公式
如果事件 在一次试验中发生的概率是
在一次试验中发生的概率是 ,那么
,那么

 次独立重复试验中事件
次独立重复试验中事件 恰好发生
恰好发生 次的概率
其中
次的概率
其中 表示球的半径
表示球的半径

第一部分 选择题(共50分)
一.选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的
1、设复数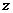 满足关系式
满足关系式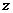 +│
+│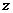 │=2+
│=2+ ,那么
,那么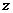 等于( )
w.w.w.k.s.5.u.c.o.m
等于( )
w.w.w.k.s.5.u.c.o.m
(A) - +
+ ;(B)
;(B)  -
- ;(C) -
;(C) - -
- ; (D)
; (D)  +
+ .
.
2 设函数
设函数 为 ( )
为 ( )
 A.周期函数,最小正周期为
A.周期函数,最小正周期为 B.周期函数,最小正周期为
B.周期函数,最小正周期为
C.周期函数,数小正周期为 D.非周期函数
D.非周期函数
3、设 则以下不等式中不恒成立的是 ( )
则以下不等式中不恒成立的是 ( )
A. ; B.
; B. ;
;
C. ; D.
; D.
4、如果 的展开式中各项系数之和为128,则展开式中的系数是( )
的展开式中各项系数之和为128,则展开式中的系数是( )
(A)7 (B)-7 (C)21 (D)-21
5、若直线 与直线
与直线 的交点位于第一象限,则直线
的交点位于第一象限,则直线 的倾斜角的取值范围是 ( )
的倾斜角的取值范围是 ( )
(A) , (B)
, (B) ,
,
(C)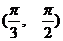 , (D)
, (D)
6、 如果 ,
, ,…,
,…, 为各项都大于零的等差数列,公差
为各项都大于零的等差数列,公差 ,则
,则
(A)


 ;(B)
;(B)


 ;(C)
;(C) +
+

 +
+ ;(D)
;(D)
 =
= .
.
7、设三棱柱ABC―A1B
A. B.
B. C.
C. D.
D.
 8、函数
8、函数 的部分图象如图,则( )
的部分图象如图,则( )
A. ; B.
; B. ;
;
C. ; D.
; D.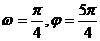
9、若椭圆经过原点,且焦点F1(1,0),F2(3,0),则其离心率为 ( )
A、 B、
B、 C、
C、 D、
D、
10、《中华人民共和国个人所得税法》规定,公民全月工资、薪金所得不超过800元的部分不必纳税,超过800元的部分为全月应纳税所得额.此项税款按下表分段累进计算:
全月应纳税所得额
税率
不超过500元的部分
5%
超过500元至2000元的部分
10%
超过2000元至5000元的部分
15%
……
…
某人一月份应交纳此项税款26.78元,则他的当月工资、薪金所得介于
 800~900元
800~900元
 900~1200元
900~1200元
 1200~1500元
1200~1500元
 1500~2800元
1500~2800元
第二部分 非选择题(共100分)
二、填空题:本大题共5小题,其中14~15题是选做题,考生只能选做一题,两题全答的,只计算前一题得分.每小题5分,满分20分.
11、已知集合为 ,它的所有的三个元素的子集的和是
,它的所有的三个元素的子集的和是 ,则
,则 =
。
=
。
12、若函数 上为增函数,则实数a、b的取值范围是___________;
上为增函数,则实数a、b的取值范围是___________;
13、椭圆 的焦点为
的焦点为 ,点P为其上的动点,当
,点P为其上的动点,当 为钝角时,点P横坐标的取值范围是_______________________;
为钝角时,点P横坐标的取值范围是_______________________;
 14、(坐标系与参数方程选做题) 极坐标系中,曲线
14、(坐标系与参数方程选做题) 极坐标系中,曲线 和
和 相交于点
相交于点 ,则
,则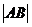 =
;
=
;
15.(几何证明选讲选做题) 如图:PA与圆O相切于A,PCB为圆O的割线,
并且不过圆心O,已知∠BPA= , PA=
, PA= ,PC=1,
,PC=1,
则圆O的半径等于 .
三.解答题:本大题共6小题,共80分,解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
已知:复数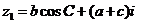 ,
, ,且
,且 ,其中
,其中 、
、 为△ABC的内角,
为△ABC的内角, 、
、 、
、 为角
为角 、
、 、
、 所对的边.
所对的边.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ) 若 ,求△ABC的面积.
,求△ABC的面积.
17.(本小题满分12分)
某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金 元,答对问题B可获奖金2
元,答对问题B可获奖金2 元;先答哪个题由观众自由选择;只有第一个问题答对,才能再答第二个问题,否则终止答题.设某幸运观众答对问题A、B的概率分别为
元;先答哪个题由观众自由选择;只有第一个问题答对,才能再答第二个问题,否则终止答题.设某幸运观众答对问题A、B的概率分别为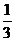 、
、 .你觉得他应先回答哪个问题才能使获得奖金的期望较大?说明理由.
.你觉得他应先回答哪个问题才能使获得奖金的期望较大?说明理由.
18.(本小题满分14分)
在以O为原点的直角坐标系中,点A(4,-3)为△OAB的直角顶点,已知|AB|=2|OA|,且点B的纵坐标大于0。
(Ⅰ)求 的坐标;
的坐标;
(Ⅱ)求圆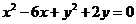 关于直线OB对称的圆的方程。
关于直线OB对称的圆的方程。
19.(本小题满分14分)
已知函数f(x)的定义域为R,对任意的 ,且当
,且当 时,
时, .
.
(Ⅰ)求证:函数f(x)为奇函数;
(Ⅱ)求证:
(Ⅲ)求函数 在区间[-n,n](n
在区间[-n,n](n )上的最大值和最小值。
)上的最大值和最小值。
20.(本小题满分14分)
如图,已知三棱柱ABC-A1B
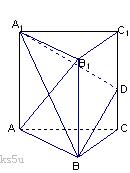 B沿棱柱侧面经过棱C C1到点A1的最短路线长为
B沿棱柱侧面经过棱C C1到点A1的最短路线长为 ,设这条最短路线与CC1的交
,设这条最短路线与CC1的交
点为D.
(1)求三棱柱ABC-A1B
(2)在平面A1BD内是否存在过点D的直线与平面ABC平行?证明你的判断;
(3)证明:平面A1BD⊥平面A1ABB1.
2. (本小题满分14分)
已知函数
(Ⅰ)若函数y=f(x)的图象切x轴于点(2,0),求a、b的值;
(Ⅱ)设函数y=f(x)  的图象上任意一点的切线斜率为k,试求
的图象上任意一点的切线斜率为k,试求 的充要条件;
的充要条件;
(Ⅲ)若函数y=f(x)的图象上任意不同的两点的连线的斜率小于1,求证 。
。
一.选择题:DBBCB BCCCC
解析:1:因为 =(2 -│
=(2 -│ │)+
│)+  ,由选择支知│
,由选择支知│ │<2,所以
│<2,所以 的实部为正数,虚部为1,根据这个隐含条件,(A),(B),(C)均可筛去,所以选(D).
的实部为正数,虚部为1,根据这个隐含条件,(A),(B),(C)均可筛去,所以选(D).
2:先将周期最小的选项(A)的周期T= 代入
代入 检验,不成立则排除(A);再检验(B)成立. 所以选(B).
检验,不成立则排除(A);再检验(B)成立. 所以选(B).
3:∵ ∴可取
∴可取 代入四个选项验证,发现B错误,∴应选(B).
代入四个选项验证,发现B错误,∴应选(B).
4:“ 的展开式中各项系数之和为
的展开式中各项系数之和为
由通项公式Tr+1= =
= ,
,
令7-=-3,解得r=6,此时T7= ,故选C

5:作两直线的图象,从图中可以看出:
直线 的倾斜角的取值范围应选(B).
的倾斜角的取值范围应选(B).
6:取特殊数列 =
= ,排除(A)、(C)、(D). ∴选(B).
,排除(A)、(C)、(D). ∴选(B).
7:如图所示,
作
∴柱体体积

 故选C.
故选C.
8:由图象可知,x=1时 =1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
=1. 由此可排除(A)、(D);再由周期T=8,可排除(B).
∴应选(C).
9:利用椭圆的定义可得 故离心率
故离心率 故选C。
故选C。
10:设某人当月工资为1200元或1500元,则其应纳税款分别为:400 5%=20元,500
5%=20元,500 5%+200
5%+200 10%=45元,可排除
10%=45元,可排除 、
、 、
、 .故选
.故选 .
.
二.填空题:11、2; 12、a>0且 ;13、
;13、 ;14、
;14、 ;15、7;
;15、7;
解析:11:因为包含了 任意一个元素
任意一个元素 的三元素集合共
的三元素集合共 个,所以在
个,所以在 中,每个元素都出现了
中,每个元素都出现了 次,所以
次,所以

 ,所以
,所以
 。
。
12:由已知可画出下图,符合题设,故a>0且 。
。
13:设P(x,y),则当 时,点P的轨迹为
时,点P的轨迹为 ,由此可得点P的横坐标
,由此可得点P的横坐标 。
。
又当P在x轴上时, ,点P在y轴上时,
,点P在y轴上时, 为钝角,由此可得点P横坐标的取值范围是:
为钝角,由此可得点P横坐标的取值范围是: ;
;
 14.解:在平面直角坐标系中,曲线
14.解:在平面直角坐标系中,曲线 和
和 分别表示圆
分别表示圆 和直线
和直线 ,易知
,易知 =
=
15.解:  由圆的性质PA
由圆的性质PA =PC?PB,得,PB=12,连接OA并反向延长
=PC?PB,得,PB=12,连接OA并反向延长
交圆于点E,在直角三角形APD中可以求得PD=4,DA=2,故CD=3,
DB=8,J记圆的半径为R,由于ED?DA=CD?DB
因此,(2R-2) ?2=3?8,解得R=7
三.解答题:
16.解:(Ⅰ)∵ ∴
∴ ----①,
----①, ----②
----②
由①得 ------③
------③
在△ABC中,由正弦定理得 =
= ,设
,设
 =
=
则 ,代入③得
,代入③得

∵  ∴
∴ ∴
∴ ,∵
,∵ ∴
∴ ……………………6分
……………………6分
(Ⅱ) ∵ ,由余弦定理得
,由余弦定理得

 ,--④
,--④
由②得 -⑤ 由④⑤得
-⑤ 由④⑤得 ,∴
,∴ =
= . ……………………………12分
. ……………………………12分
17.解:设该观众先答A题所获奖金为 元,先答B题所获奖金为
元,先答B题所获奖金为 元,………………………1分
元,………………………1分
依题意可得 可能取的值为:0,
可能取的值为:0,  ,3
,3 ,
,  的可能取值为:0,2
的可能取值为:0,2 ,3
,3
………………………2分
∵ ,
, ,
, ,
,
∴ ,
………………………6分
,
………………………6分
∵ ,
, ,
, 
∴ ………………………10分
………………………10分
∵
 ∴
∴ ,即
,即
∴该观众应先回答B题所获奖金的期望较大. ……………………………12分
18.解:(Ⅰ)设 ,由
,由 得
得 ,解得
,解得 或
或 ,若
,若 则
则 与
与 矛盾,所以
矛盾,所以 不合舍去。
不合舍去。
即 。---------------------------------------------------------------------------6
。---------------------------------------------------------------------------6
(Ⅱ)圆 即
即 ,其圆心为C(3,-1),半径
,其圆心为C(3,-1),半径 ,
,
∴直线OB的方程为 ,-----------------------------------------------------------------10
,-----------------------------------------------------------------10
设圆心C(3,-1)关于直线 的对称点的坐标为(a,b),则
的对称点的坐标为(a,b),则

解得: ,则所求的圆的方程为
,则所求的圆的方程为 。-----------------------------14
。-----------------------------14
19.(Ⅰ)证明:∵对任意的 ①
①
令 得
得 ②…………1分
②…………1分
令 得
得 ……………………2分
……………………2分
∴ 由②得
由②得
∴函数 为奇函数………………………………3分
为奇函数………………………………3分
(Ⅱ)证明:(1)当n=1时等式显然成立
(2)假设当n=k(k )时等式成立,即
)时等式成立,即 ,…………4分
,…………4分
则当n=k+1时有
 ,由①得
,由①得 ………………6分
………………6分
∵ ∴
∴
∴当n=k+1时,等式成立。
综(1)、(2)知对任意的 ,
, 成立。………………8分
成立。………………8分
(Ⅲ)解:设 ,因函数
,因函数 为奇函数,结合①得
为奇函数,结合①得
 =
= ,……………………9分
,……………………9分
∵
又∵当 时,
时,
∴
 ,∴
,∴
∴函数 在R上单调递减…………………………………………12分
在R上单调递减…………………………………………12分
∴

由(2)的结论得 ,
,
∵ ,∴
,∴ =-2n
=-2n
∵函数 为奇函数,∴
为奇函数,∴
∴
 ,
, =2n。……………………14分
=2n。……………………14分
20.解:(1)如图,将侧面BB
∵CD∥AA1 ∴D为CC1的中点,……………………………2分
在Rt△A1AB2中,由勾股定理得 ,
,
即 解得
解得 ,……………………4分
,……………………4分
∵ ∴
∴ ……………………………………6分
……………………………………6分
(2)设A1B与AB1的交点为O,连结BB2,OD,则 ……………………………7分
……………………………7分
∵ 平面
平面 ,
, 平面
平面 ∴
∴ 平面
平面 ,
,
即在平面A1BD内存在过点D的直线与平面ABC平行 ……………………………9分
(3)连结AD,B1D ∵ ≌
≌ ≌
≌
∴ ∴
∴ ……………………………11分
……………………………11分
∵ ∴
∴ 平面A1ABB1 ……………………………13分
平面A1ABB1 ……………………………13分
又∵ 平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
平面A1BD ∴平面A1BD⊥平面A1ABB1 ……………………………………14分
21.解:(Ⅰ)
 …………………………………………1分
…………………………………………1分
由 得
得 , ………………………………………………2分
, ………………………………………………2分
又 得
得 ……………………………………………………3分
……………………………………………………3分
(Ⅱ) k=
k=
 ,
,
 对任意的
对任意的
 ,即
,即 对任意的
对任意的 恒成立……4分
恒成立……4分
等价于 对任意的
对任意的 恒成立。…………………………5分
恒成立。…………………………5分
令g(x)= ,h(x)=
,h(x)= ,
,
则 ,
, …………………………………………6分
…………………………………………6分
 ,当且仅当
,当且仅当 时“=”成立,
时“=”成立,
 …………7分
…………7分
 h(x)=
h(x)= 在(0,1)上为增函数,
在(0,1)上为增函数, h(x)max<2……………………………8分
h(x)max<2……………………………8分

 ……………………………………………………………………9分
……………………………………………………………………9分
(Ⅲ)设 则
则 =
= ……10分
……10分
即 ,对
,对 恒成立…………………………11分
恒成立…………………………11分

 ,对
,对 恒成立
恒成立
即 对
对 恒成立…………………………13分
恒成立…………………………13分


解得 ……………………………………………………14分
……………………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com