
崇文区2008―2009学年度第二学期高三统一练(一)
数 学(理科) 2009.3
本试卷分第I卷(选择题)和第Ⅱ卷(非选择题)两部分,第I卷1至2页,第Ⅱ卷3至9爷页,共150分。考试时间120分钟。考试结束,将本试卷和答题卡一并交回。
第I卷(选择题 共40分)
注意事项:
1.答第I卷前,考生务必将自己的姓名、准考证号、考试科目涂写在答题卡上。
2.每小题选出答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。不能答在试卷上。
一、选择题:本大题共8小题,每小题5分,共40分。在每小题给出的四个选项中,只有
1.设集合 则
则
A. B.
B. C.
C. D.
D.
2.抛物线 的焦点坐标是
的焦点坐标是
A. B.
B. C.(0,1) D.(1,0)
C.(0,1) D.(1,0)
3.已知 ,则
,则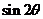 的值为
的值为
A. B.
B. C.
C. D.
D.
4.若函数 的图象与函数
的图象与函数 的图象关于直线
的图象关于直线 对称,则
对称,则
A. B.
B. C.
C. D.
D.
5.已知 是两条不重合的直线,
是两条不重合的直线, 是三个重合的平面,则
是三个重合的平面,则 的一个充分条件是
的一个充分条件是
A. B.
B.
C. D.
D. 是异面直线,
是异面直线,
 6.在如图所示的坐标平面的可行域内(阴影部分且包括边
6.在如图所示的坐标平面的可行域内(阴影部分且包括边
界),若目标函数 取得最小值的最优解有无数个,
取得最小值的最优解有无数个,
则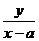 的最大值是
的最大值是
A. B.
B.
C. D.
D.
7.直角坐标系中横坐标、纵坐标均为整数的点称为格点,如果函数 的图象恰好通过
的图象恰好通过 个格点,则称函数
个格点,则称函数 为
为 阶格点函数,下列函数:
阶格点函数,下列函数:
① ; ②
; ② ; ③
; ③ ; ④
; ④
其中是一阶格点函数的有
A.①② B.①④ C.①②④ D.①②③④
8.已知函数 的定义域为
的定义域为 ,当
,当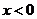 时,
时, ,且对任意的
,且对任意的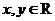 ,等式
,等式 成立,若数列
成立,若数列 满足
满足 ,且
,且
 则
则 的值为
的值为
A.4016 B.4017 C.4018 D.4019
二、填空题:本大题共6小题,每小题5分,共30分。把答案填在题中横线上。
9.已知 是复数,i是虚数单位,若
是复数,i是虚数单位,若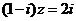 ,则
,则 =__________________________
=__________________________
 10.极限
10.极限
11.如图,等腰梯形 中,
中, ,
, 分别是
分别是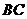 上三等分点,
上三等分点,
 ,若把三角形
,若把三角形 和
和 分别沿
分别沿
和 折起,使得
折起,使得 两点重合于一点
两点重合于一点 ,则二面角
,则二面角
 的大小为_________________________
的大小为_________________________
12.设集合 ,定义在
,定义在 上的映射
上的映射 ,满足对任意
,满足对任意 ,均有
,均有
 且
且 ,若
,若
 不共线,则
不共线,则 ______;
______;
若 ,且
,且 ,则
,则 =____________________________。
=____________________________。
13.已知 是椭圆
是椭圆 =1(
=1( 的右焦点,以坐标原点
的右焦点,以坐标原点 为圆心,
为圆心, 为半径作圆
为半径作圆 ,过
,过 垂直于
垂直于 轴的直线与圆
轴的直线与圆 交于
交于 两点,过点
两点,过点 作圆
作圆 的切线交
的切线交 轴于点
轴于点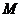 若直线
若直线 过点
过点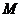 且垂直于
且垂直于 轴,则直线
轴,则直线 的方程为_______________________;若
的方程为_______________________;若 =
= ,则椭圆的离心率等于______________。
,则椭圆的离心率等于______________。
14.对于集合 的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合|1,2,4,6,9|的交替和是9-6+4-2+1=6,集合
的每一个非空子集,定义一个“交替和”如下:按照递减的次序重新排列该子集,然后从最大数开始交替地减,加后继的数,例如集合|1,2,4,6,9|的交替和是9-6+4-2+1=6,集合 的交替和为5,当集合
的交替和为5,当集合 中的
中的 时,集合
时,集合 的所有非空子集为|1|,|2|,|1,2|,则它的“交替和”的总和
的所有非空子集为|1|,|2|,|1,2|,则它的“交替和”的总和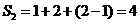 请你尝试对
请你尝试对 的情况,计算它的“交替和”的总和
的情况,计算它的“交替和”的总和 ,并根据其结果猜测集合
,并根据其结果猜测集合 的每一个非空子集的“交替和”的总和
的每一个非空子集的“交替和”的总和 =________________。
=________________。
三、解答题:本大题共6小题,共80分。解答应写出文字说明,证明过程或演算步骤。
15.(本小题满分13分)
在 中,角
中,角 所对的边分别为a,b,c已知向量
所对的边分别为a,b,c已知向量
 满足
满足
(I)求 的大小;
的大小;
(Ⅱ)求 的值
的值
17.(本小题满分13分)
高三(1)班和高三(2)班各已选出3名学生组成代表队,进行乒乓球对抗赛,比赛规则是:
①按“单打、双打、单打”顺序进行三盘比赛;
②代表队中每名队员至少参加一盘比赛,但不得参加两盘单打比赛;
③先胜两盘的队获胜,比赛结束,已知每盘比赛双方胜出的概率均为
(I)根据比赛规则,高三(1)班代表队共可排出多少种不同的出场阵容?
(Ⅱ)高三(1)班代表队连胜两盘的概率为多少?
(Ⅲ)设高三(1)班代表队获胜的盘数为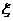 ,求
,求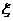 的分布列和数学期望。
的分布列和数学期望。
18.(本小题满分13分)
已知函数 且
且
(I)若曲线 在点P
在点P 处的切线垂直于
处的切线垂直于 轴,求实数
轴,求实数 的值;
的值;
(Ⅱ)当 时,求函数
时,求函数 的最大值和最小值。
的最大值和最小值。
19.(本小题满分14分)
已知动圆 过点
过点 并且与圆
并且与圆 想外切,动圆圆心
想外切,动圆圆心 的轨迹为
的轨迹为 ,轨迹
,轨迹 与
与 轴的交点为D
轴的交点为D
(I)求轨迹 的方程;
的方程;
(Ⅱ)设直线 过点
过点 且与轨迹
且与轨迹 有两个不同的交点
有两个不同的交点 求直线
求直线 的斜率
的斜率 的取值范围;
的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若 ,证明直线
,证明直线 过定点,并求出这个定点的坐标。
过定点,并求出这个定点的坐标。
20.(本小题满分13分)
已知函数 数列
数列 满足条件:
满足条件: ,
,

(I)求数列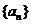 的通项公式;
的通项公式;
(Ⅱ)求数列 的前项
的前项 和
和 ,并求使得
,并求使得 对任意
对任意 都成立的最大正整数m;
都成立的最大正整数m;
(Ⅲ)求证:







湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com