|
试题详情
试题详情
试题详情
试题详情
试题详情
12.已知O是平面上的一个定点,A、B、C是平面上不共线的三个点,动点P满足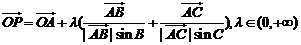 ,则动点P的轨迹一定通过△ABC的( ) ,则动点P的轨迹一定通过△ABC的( ) 试题详情
A.垂心 B.重心 C.外心 D.内心 试题详情
二、填空题:(本大题共4小题,每小题4分,共16分,请把答案填在答题卡上。)
试题详情
试题详情
试题详情
16.给出下列命题: 试题详情
试题详情
试题详情
C.底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥。 试题详情
试题详情
其中正确的命题是
(把所有正确的命题的选项都填上) 试题详情
三、解答题:(本大题共6小题,共74分。解答应写出文字说明,证明过程或演算步骤。) 17.(本小题满分12分) 试题详情
试题详情
(Ⅰ)求角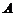 的大小; 的大小; 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
18.(本小题满分12分) 试题详情
试题详情
(Ⅰ)求在5月13日恰有1支队伍抵达灾区的概率; 试题详情
(Ⅱ)求在5月13日抵达灾区的队伍数为多少时概率最大。 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
19.(本小题满分12分) 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
20.(本小题满分12分) 试题详情
如图,已知正三棱柱ABC-A1B1C1的侧棱长和底面边长均为1, 试题详情
M是底面BC边上的中点,N是侧棱CC1上的点,且CN=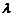 NC1. NC1. 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
21.(本小题满分12分) 试题详情
试题详情
试题详情
试题详情
(Ⅰ)求 的解析式; 的解析式; 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(Ⅱ)试根据(Ⅰ)中的结论猜测:椭圆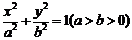 的“左特征点”M是一个怎样的点?并证明你的结论. 的“左特征点”M是一个怎样的点?并证明你的结论. 2009届师大附中、鹰潭一中高三联考 试题详情
一、选择题 1--5 ADACB 6--10 ABACD 11―12 CB 二、填空题 13.8 14.7 15.12 16.AB 三、解答题 17.解:(Ⅰ)  , ,  , ,
 .…………………………(4分) .…………………………(4分)
  , ,  .………………………(6分) .………………………(6分)
(Ⅱ)由余弦定理 ,得 ,得  .………(8分) .………(8分)  , ,  . .
  所以 所以 的最小值为 的最小值为 ,当且仅当 ,当且仅当 时取等号.………………(12分) 时取等号.………………(12分)
 18.(Ⅰ)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且 18.(Ⅰ)解法一:依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且 .……………………………(2分) .……………………………(2分)
在5月13日恰有1支队伍抵达灾区的概率是  .……………………(6分) .……………………(6分)
解法二:在5月13日恰有1支队伍抵达灾区的概率是  .…………(6分) .…………(6分)
(Ⅱ)依据题意,因为队伍从水路或陆路抵达灾区的概率相等,则将“队伍从水路或陆路抵达灾区”视为同一个事件. 记“队伍从水路或陆路抵达灾区”为事件C,且B、C相互独立,而且 . . 设5月13日抵达灾区的队伍数为 ,则 ,则 =0、1、2、3、4. ……………………(7分) =0、1、2、3、4. ……………………(7分) 由已知有: ; ;  ; ;
 ; ;
 ; ;
 . .
答:在5月13日抵达灾区的队伍数为2时概率最大……………………(12分) 19. (I)由已知a2-a1=-2, a3-a2=-1, -1-(-2)=1 ∴an+1-an=(a2-a1)+(n-1)?1=n-3 n≥2时,an=( an-an-1)+( an-1-an-2)+…+( a3-a2)+( a2-a1)+ a1 =(n-4)+(n-5) +…+(-1)+(-2)+6 = n=1也合适. ∴an= (n∈N*) ……………………3分 (n∈N*) ……………………3分 又b1-2=4、b2-2=2 .而 ∴bn-2=(b1-2)?( ∴bn-2=(b1-2)?( )n-1即bn=2+8?( )n-1即bn=2+8?( )n……(6分) )n……(6分) ∴数列{an}、{bn}的通项公式为:an= ,bn=2+( ,bn=2+( )n-3 )n-3  (II)设 (II)设
  当k≥4时 当k≥4时 为k的增函数,-8?( 为k的增函数,-8?( )k也为k的增函数,而f(4)= )k也为k的增函数,而f(4)= 
 ∴当k≥4时ak-bk≥ ∴当k≥4时ak-bk≥ ………………10分 ………………10分
又f(1)=f(2)=f(3)=0 ∴不存在k, 使f(k)∈(0, )…………12分 )…………12分 20解法1:(Ⅰ)因为M是底面BC边上的中点,且AB=AC,所以AM BC, BC,  在正三棱柱ABC-A1B1C1中, 在正三棱柱ABC-A1B1C1中, 底面 底面 , ,  AM AM  又 又 .所以AM .所以AM 平面 平面  . .
(或:连结 , , 又 又 , , .)…………(5分) .)…………(5分) (II)因为AM 平面 平面  且 M M 平面 平面  ,NM ,NM 平面 平面  ∴AM  M, AM M, AM NM, NM, ∴  MN为二面角 MN为二面角 ―AM―N的平面角. …………(7分) ―AM―N的平面角. …………(7分) ∴ ,设C1N= ,设C1N= ,则CN=1- ,则CN=1- 又 M= M=  ,MN= ,MN= , ,  连 连 N,得 N,得 N= N= , ,
在  MN中,由余弦定理得 MN中,由余弦定理得  , …(10分) , …(10分)
得 = = .故 .故 =2. … (12分) =2. … (12分) 解法2:(Ⅰ)建立如图所示的空间直角坐标系,则 (0,0,1),M(0, (0,0,1),M(0, ,0), ,0), C(0,1,0), A ( ),设N (0,1,a) ,所以, ),设N (0,1,a) ,所以,  , , , ,
因为 所以 所以 ,同法可得 ,同法可得 .又 .又 故AM 故AM 面BC 面BC  . . (II)由(Ⅰ)知? ?为二面角 ?为二面角 ―AM―N的平面角,以下同法一. ―AM―N的平面角,以下同法一. 21解(Ⅰ)由已知  ∴ ∴ ∴ ∴ ………………(2分) ………………(2分)
又 且 且 ∴ ∴ (舍去 (舍去 ) ) ∴ …(4分) …(4分) (Ⅱ)令 即 即 的增区间为 的增区间为 、 、 ∵ 在区间 在区间 上是增函数 上是增函数 ∴ 或 或 则 则 或 或 ……(8分) ……(8分) (Ⅲ)令 或 或 ∵ ∴ 在 在 上的最大值为4,最小值为0………………(10分) 上的最大值为4,最小值为0………………(10分) ∴ 、 、 时, 时, ……………(12分) ……………(12分) 22.解 (1)设 为椭圆 为椭圆 的左特征点,椭圆的左焦点为 的左特征点,椭圆的左焦点为 ,可设直线 ,可设直线 的方程为 的方程为 .并将它代入 .并将它代入 得: 得: ,即 ,即 .设 .设 ,则 ,则 ,……(3分) ,……(3分) ∵ 被 被 轴平分,∴ 轴平分,∴ .即 .即 . . 即 ,∴ ,∴ .……………(5分) .……………(5分) 于是 . . ∵ ,即 ,即 .………………(7分) .………………(7分) (2)对于椭圆 .于是猜想:椭圆 .于是猜想:椭圆 的“左特征点”是椭圆的左准线与 的“左特征点”是椭圆的左准线与 轴的交点. ………………(9分) 轴的交点. ………………(9分)  证明:设椭圆的左准线 证明:设椭圆的左准线 与 与 轴相交于M点,过A,B分别作 轴相交于M点,过A,B分别作 的垂线,垂足分别为C,D. 的垂线,垂足分别为C,D.
据椭圆第二定义: ∵ ∵  于是 即 即 .∴ .∴ ,又 ,又 均为锐角,∴ 均为锐角,∴ ,∴ ,∴ . . ∴ 的平分线.故M为椭圆的“左特征点”. ………(14分) 的平分线.故M为椭圆的“左特征点”. ………(14分)
| 



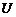 ={1,2,3,4,5,6},集合
={1,2,3,4,5,6},集合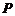 ={1,2,3,4},
={1,2,3,4},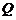 ={3,4,5,6},则
={3,4,5,6},则 =( )
=( )
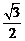 D.1
D.1
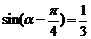 ,则
,则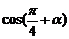 的值等于( )
的值等于( )
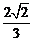 B.-
B.-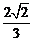 C.
C.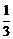 D.-
D.-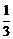

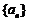 是等差数列,且
是等差数列,且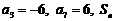 是数列
是数列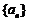 的前n项和,则( )
的前n项和,则( )
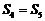 B.
B.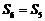 C.
C. D.
D.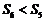

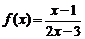 的反函数是
的反函数是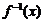 ,则
,则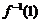 =( )
=( )

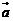 与
与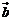 的夹角为
的夹角为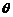 ,定义
,定义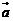 与
与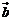 的“向量积”:
的“向量积”: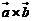 是一个向量,它的模
是一个向量,它的模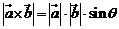 ,若
,若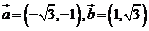 ,则
,则 ( )
( )
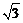 B.2 C.
B.2 C.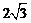 D.4
D.4
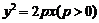 的焦点作直线交抛物线于
的焦点作直线交抛物线于 ,
,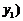 、
、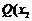 ,
,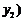 两点,若
两点,若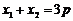 ,则
,则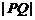 等于( )
等于( )

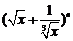 的各项系数之和大于
的各项系数之和大于 ,小于
,小于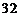 ,则展开式中系数最大的项是( )
,则展开式中系数最大的项是( ) 
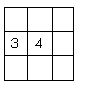 A.
A.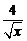 B.
B.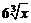 C.
C.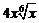 D.
D.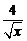 或
或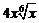



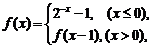 若方程
若方程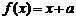 有且只有两个不相等的实数根,则实数
有且只有两个不相等的实数根,则实数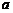 的取值范围为( )
的取值范围为( )
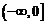 B.
B.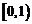 C.
C.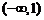 D.
D.