
湖南省衡阳市祁东县育贤中学高三文科数学试题(2007年2月)
(按全国卷文科格式加以改编)
湖南省衡阳市祁东县育贤中学 高明生 (421600)
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。第Ⅰ卷1至12题。第Ⅱ卷13至22题。
参考公式:
如果时间A、B互斥,那么
如果时间A、B相互独立,那么
如果事件A在一次试验中发生的概率是P,那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 ,其中R表示球的半径
,其中R表示球的半径
球的体积公式 ,其中R表示球的半径
,其中R表示球的半径
第Ⅰ卷
本卷共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
一、选择题
1.已知: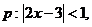

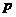 是
是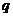 的( )
的( )
A.充分不必要条件 B。必要不充分条件 C.充要条件 D。既不充分也不必要条件
2.点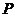 在曲线
在曲线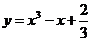 上移动,在点
上移动,在点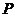 处的切线的倾斜角为
处的切线的倾斜角为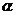 ,则
,则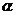 的取值范围是( )
的取值范围是( )
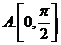
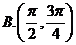
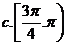
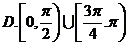
3.已知函数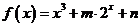 是奇函数,则( )
是奇函数,则( )
A. B。
B。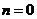 C。
C。 且
且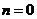 D。
D。 或
或
4.向量 ,若
,若 与
与 共线(其中
共线(其中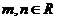 且
且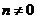 ),则
),则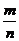 等于( )
等于( )
A.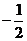 B。
B。 D。
D。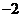
5.对于实数 ,符号
,符号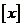 表示不超过
表示不超过 的最大整数,例如
的最大整数,例如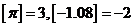 ,定义函数
,定义函数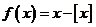 ,则下列命题中正确的是( )
,则下列命题中正确的是( )
A. B。方程
B。方程 有且仅有一个解
有且仅有一个解
C。函数 是周期函数
D。函数
是周期函数
D。函数 是增函数
是增函数
6.设 为椭圆
为椭圆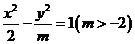 的离心率,且
的离心率,且 ,则实数
,则实数 的取值范围为( )
的取值范围为( )

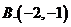

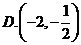
7.已知 是定义在R上的周期为2的偶函数,当
是定义在R上的周期为2的偶函数,当 时,
时, 设
设 ,则
,则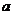 、
、 、
、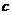 的大小关系为( )
的大小关系为( )
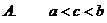
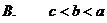
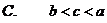
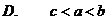
8.线段AB长为2,两个端点A、B分别在一个直二面角的两个面上,AB和两个面所成的角分别是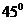 和
和 ,那么点A、B在这个二面角的棱上的射影C、D间的距离是( )
,那么点A、B在这个二面角的棱上的射影C、D间的距离是( )
A.1 B。 C。2 D。
C。2 D。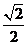
9.已知非零向量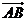 与
与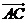 满足
满足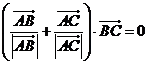 且
且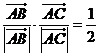 ,则
,则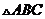 为( )
为( )
A.三边均不相等的三角形 B。直角三角形
C.等腰非等边三角形 D。等边三角形

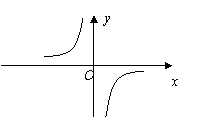 10.函数y=f(x)与y=g(x)的图象如下图:
10.函数y=f(x)与y=g(x)的图象如下图:
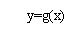
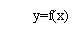
 则函数y=f(x)g(x)的图象可能为( )
则函数y=f(x)g(x)的图象可能为( )
A B C D
11..由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为( )
A. 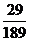 B.
B. 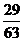 C.
C. 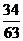 D.
D. 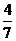
12.给出下列四个命题:
①若函数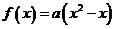 在区间
在区间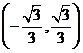 为减函数,则
为减函数,则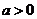 ;
;
②函数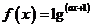 的定义域是
的定义域是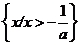 ;
;
③当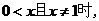
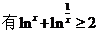 ;
;
④若M是圆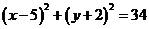 上的任意一点,
上的任意一点,
则点M关于 的对称点
的对称点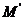 也在该圆上。
也在该圆上。
所有正确命题的序号是( )
A.①④ B。②④ C。①③ D。③④
第Ⅱ卷
注意事项:
请用黑色签字笔在答题卡上各题的答题区域内作答,在试题卷上作答无效。
本卷共10小题,共90分。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上。
13.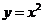 上一点
上一点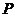 (非原点),在
(非原点),在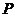 处引切线交
处引切线交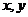 轴于
轴于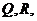 则
则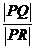 = 。
= 。
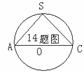 14.正四棱锥S―ABCD的5个顶点都在球O的表面上,过球心O的一个截面如图,棱锥的底面边长为1,则球心O到侧面SAB的距离为
。
14.正四棱锥S―ABCD的5个顶点都在球O的表面上,过球心O的一个截面如图,棱锥的底面边长为1,则球心O到侧面SAB的距离为
。
15.二项式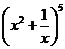 的展开式中
的展开式中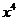 的系数为
。
的系数为
。
16.如果函数 的导函数的图象如右图所示,给出下列判断:
的导函数的图象如右图所示,给出下列判断:
①函数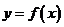 在区间
在区间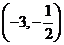 内单调递增;
内单调递增;
②函数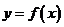 在区间
在区间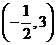 内单调递减;
内单调递减;
③函数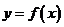 在区间
在区间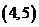 内单调递增;
内单调递增;
④当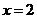 时,函数
时,函数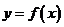 有极小值;
有极小值;
⑤当 时,函数
时,函数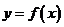 有极大值;
有极大值;
则上述判断中正确的是 。
(17)(本小题满分12分)求由正整数组成的集合S,使S中的元素之和等于元素之积。
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
(18)(本小题满分12分)已知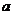 、
、 为非负数,
为非负数,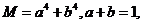 求
求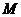 的最值。
的最值。
(19)(本小题满分12分)过正方体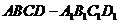 的8个顶点中任意两点的直线,与平面
的8个顶点中任意两点的直线,与平面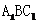 垂直的直线条数有多少?并加以证明。
垂直的直线条数有多少?并加以证明。
(20)。(本小题满分12分)湖南是劳务输出大省,据劳动村村长统计,第一季度,劳动村有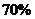 的农民在外打工,第二季度,劳动村有
的农民在外打工,第二季度,劳动村有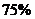 的农民在外打工,第三季度,劳动村有
的农民在外打工,第三季度,劳动村有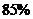 的农民在外打工,第四季度,劳动村有
的农民在外打工,第四季度,劳动村有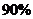 的农民在外打工,问劳动村至少有百分之几的农民全年在外打工?
的农民在外打工,问劳动村至少有百分之几的农民全年在外打工?
(21)、(本小题满分14分)两根等长的绳子挂一个物体,绳子受到的拉力大小为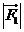 ,物体的重量为
,物体的重量为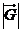 ,两绳子间的夹角为
,两绳子间的夹角为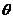 。
。
① 求绳子受到的拉力大小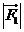 与两绳子间的夹角
与两绳子间的夹角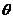 的关系;
的关系;
② 当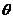 逐渐增大时,
逐渐增大时,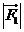 的大小怎样变化?
的大小怎样变化?
③ 当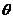 为何值时,
为何值时,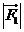 最小,最小值是多少?
最小,最小值是多少?
④当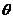 为何值时,
为何值时,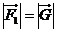 ?
?
(22)、(本小题满分12分)给定抛物线C:y2=4x,F是C的焦点,过点F的直线l与C相交于A、B两点。
(Ⅰ)设l的斜率为1,求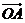 与
与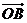 的夹角的大小;
的夹角的大小;
(Ⅱ)设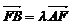 ,若λ∈[4,9],求l在y轴上截距的变化范围.
,若λ∈[4,9],求l在y轴上截距的变化范围.
湖南省衡阳市祁东县育贤中学高三文科数学试题(2007年2月)
一、选择题:本大题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.答案:A
解:依题意可知:由
 显然:
显然: 但
但 不能推出
不能推出 。
。
故选A ;
2.答案:D
解:依题意可知:设点 ,则在点P处的切线的斜率为
,则在点P处的切线的斜率为 ,即
,即 ,又
,又
故选D ;
3.答案:C
解:依题意可知:由 是奇函数,
是奇函数,


故选C ;
4.答案:A
解:依题意可知:由


故选A;
 5.答案:C
5.答案:C
解:如图:函数 是周期函数,T=1。
是周期函数,T=1。
故选C;
6.答案:A
解:依题意可知:由
 ,
,
 ,
,
又
 。
。
故选A ;
 7.答案:B
7.答案:B
解:依题意可知:由图可知:
 。
。
8.答案:A
解:依题意可知:如图,

 ,
,
则在 中,
中, ;
;
则在 中,
中, ;
;
则在 中,
中, ;
;
故选A ;
9.答案:D
解:依题意可知:因 表示与
表示与 同方向的单位向量,
同方向的单位向量,
 表示与
表示与 同方向的单位向量,故
同方向的单位向量,故
 ,而
,而



 ,
,
又( +
+ )
) ,说明
,说明 向量与
向量与 向量垂直,根据向量加法的平行四边形法则可知:
向量垂直,根据向量加法的平行四边形法则可知: 向量所在直线 过
向量所在直线 过 向量所在线段中点,根据等腰三角形三线合一的性质,可逆推
向量所在线段中点,根据等腰三角形三线合一的性质,可逆推 为等腰三角形。又
为等腰三角形。又 与
与 夹角为
夹角为 ,故
,故 为等边三角形。
为等边三角形。
故选D ;
10.答案:A
解:设 ,在
,在
 上,
上, ,
, ,
, ,排除D;在
,排除D;在
 上,
上, ,
, ,
, ,排除B与C;故选A。
,排除B与C;故选A。
11.答案:B
解法一:正方体的八个顶点可确定 条直线;
条直线; 条直线组成
条直线组成 对直线;正方体的八个顶点可确定
对直线;正方体的八个顶点可确定 个面,其中12个四点面(6个表面,4个面对角面,2个体对角面),8个三点面;每个四点面上有
个面,其中12个四点面(6个表面,4个面对角面,2个体对角面),8个三点面;每个四点面上有 条直线,6条直线组成
条直线,6条直线组成 对直线,12个四点面由12×15=180对直线组成;每个三点面上有
对直线,12个四点面由12×15=180对直线组成;每个三点面上有 条直线,3条直线组成
条直线,3条直线组成 对直线,8个三点面由8×3=24对直线组成;由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为
对直线,8个三点面由8×3=24对直线组成;由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ;
;
解法二:正方体的八个顶点可确定 个四面体,每个四面体中有三对异面直线,由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为
个四面体,每个四面体中有三对异面直线,由正方体的八个顶点中的两个所确定的所有直线中,取出两条,这两条直线是异面直线的概率为 ;
;
12.答案:A
解:①正确;①中依题意可令 ,
,
当 时,
时,
 在
在 上为减函数,
上为减函数,
又因 在区间
在区间 为减函数,故
为减函数,故 ;
;
②错误;②中 当
当
当
③错误;③中当 时,
时,
④正确;
 圆的对称轴为直径所在的直线,故原命题正确。
圆的对称轴为直径所在的直线,故原命题正确。
故答案为:A。
二、填空题:本大题共4小题,每小题4分,共16分,把答案填在横线上。
13.答案:
解:设P点的坐标为 ,则
,则
 直线PQ的方程为:
直线PQ的方程为: 即
即 ,
,
 Q点的坐标为
Q点的坐标为 ,R点的坐标为
,R点的坐标为 ,
,


故答案为: ;
;
14.答案:
解:依题意可知:正四棱锥S―ABCD的底面正方形ABCD在过球心O的大圆上,设球半径为R,AC=2R= ,
,
 ;
;
设球心O到侧面SAB的距离为 ,连接
,连接
 ,
, ,过
,过 作
作 于
于 ,
,
连接SM,则 ,
,


 ,
,
又 4
4 。
。
故答案为: ;
;
15.答案:10
解:依题意可知:由 令
令 ,故
,故 的系数为
的系数为 。
。
故答案为:10 ;
16.答案:③
解:依题意可知:①错,因在 上,
上, 为减函数,而在
为减函数,而在 上,
上, 为增函数。
为增函数。
②错,因在 上,
上, 为增函数,而在
为增函数,而在 上,
上, 为减函数。
为减函数。
③正确。因在 上,
上, 为增函数。
为增函数。
④错,因在 上,
上, 为增函数,而在
为增函数,而在 上,
上, 为减函数,故
为减函数,故 时,函数
时,函数 有极大值。
有极大值。
⑤错,因在 上,
上, 为增函数,故
为增函数,故 时,函数
时,函数 没有极大值。
没有极大值。
故答案为:③;
三、解答题:本大题共6小题,共74分,解答应写出文字说明,证明过程或演算步骤。
(17)解: ,设
,设 中有
中有 个元素,显然有
个元素,显然有 ,其中最大的一个是
,其中最大的一个是 ,由于
,由于 是正整数集合,故
是正整数集合,故 且
且 ;
;
当 时,
时, ,此时不符合题意;
,此时不符合题意;
当 时,
时, 或
或 或
或 ,显然只有
,显然只有 符合题意;
符合题意;
当 时,设
时,设 其中
其中 ,
,
此时令
 ,
,
若 ,则
,则
 ,
,
 不符合题意;
不符合题意;
若 ,由于
,由于 是正整数集合,故
是正整数集合,故 ,
,


 故
故 时不符合题意;
时不符合题意;
综上所述 。
。
(18)解:令


故当
 (19)。答:与平面
(19)。答:与平面 垂直的直线条数有1条为
垂直的直线条数有1条为 ;
;
证法一:依题意由图可知:连 ,
,

连 ,
,
 ;
;
证法二:依题意由图建立空间直角坐标系:

 ,
,
设与 垂直的法向量为
垂直的法向量为 ,则有:
,则有:

 ,而
,而 ,故
,故 。
。
(20)解:设S为劳动村全体农民的集合, 为
为 季度劳动村在外打工的农民的集合,则
季度劳动村在外打工的农民的集合,则 为
为 季度劳动村没有在外打工的农民的集合,由题意有
季度劳动村没有在外打工的农民的集合,由题意有

所以
劳动村的农民全年在外打工为 ,则
,则

 ,
,
但
 ,
,
所以
 ,
,
即
 。
。
故劳动村至少有 的农民全年在外打工。
的农民全年在外打工。
(21)解:①作图进行受力分析,如下图示;
由向量的平行四边形法则,力的平衡及解直角三角形等知识,得出:


② ∵
 ,∴
,∴
故 在
在 上为减函数,
上为减函数,
∴当 逐渐增大时,
逐渐增大时, 也逐渐增大。
也逐渐增大。
③要 最小,则
最小,则 为最大,∴当
为最大,∴当 为
为 时,
时, 最小,最小值是
最小,最小值是 。
。
④要 ,则
,则 ,∴当
,∴当 为
为 时,
时, 。
。
(22)解:(Ⅰ)C的焦点为F(1,0),直线l的斜率为1,所以l的方程为
将 代入方程
代入方程 ,并整理得
,并整理得 
设 则有
则有 



所以 夹角的大小为
夹角的大小为
(Ⅱ)由题设 得
得 
|