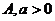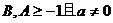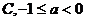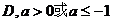|
试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
(文)函数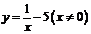 的反函数是
( ) 的反函数是
( ) 试题详情
A.在定义域内单调递减
B、在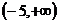 单调递增. 单调递增. 试题详情
试题详情
9、(理)已知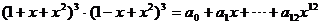 则 则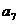 =( ) =( ) 试题详情
A、0 B、1 C、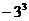 D、 D、 试题详情
(文) 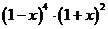 的展开式中 的展开式中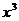 的系数为
( ) 的系数为
( ) 试题详情
A.4
B.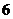 C.7 D. C.7 D.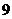 试题详情
试题详情
试题详情
试题详情
12. ( ) ( ) 试题详情
试题详情
二、填空题 13.已知A={x-y|y=x2},B={x|x2-5x-6>0},则A B=
. B=
. 试题详情
14.30名武警排成5行6列的队形,现从中选出 人,要求其中任意 人,要求其中任意 人不同行也不同列,则不同的选出方法种数为
. 人不同行也不同列,则不同的选出方法种数为
. 试题详情
15、(理)设函数 则关于x的方程|f(x)|=2x的解的个数------------------------- 试题详情
试题详情
若 ,则a1
,a2,a3的大小关系为 ,则a1
,a2,a3的大小关系为 试题详情
16. 已知曲线C:x2+ay2=a,设直线l1交曲线C于不同两点P1,P2,记线段P1P2的中点为P,直线l2过P点和坐标原点O,若对任意直线l1,都有 ,则a的值为 ,则a的值为 试题详情
三、解答题
试题详情
18. 已知:命题 :“函数 :“函数 的图象与x轴负半轴有两个不同交点”; 的图象与x轴负半轴有两个不同交点”; 试题详情
命题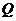 :“不等式|x-1|-1 :“不等式|x-1|-1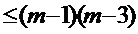 的解集为空集””.若命题 的解集为空集””.若命题 或 或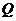 为真, 为真, 且 且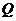 为假.求实数t的取值范围. 为假.求实数t的取值范围. 试题详情
试题详情
试题详情
试题详情
试题详情
试题详情
20.某公司今年计划投资10万元给甲、乙两地的水产养殖场,经市场营销部评估,若不受洪水影响,每投入1万元资金,在甲地可获利1.5万元,若遭受洪水影响的话,则将损失0.5万元;同样的情况,在乙地可获利1万元,否则将损失0.2万元.而气象部门的统计资料表明,甲、乙两地发生洪水的概率分别为0.6和0.5. 试题详情
(1)(文、理)若在甲、乙两地分别投资5万元,求获利12.5万元的概率. (2)若限定在两地的投资额相差不超过2万元. (理)问在甲、乙两地怎样分配资金可平均获利最大? (文)假设今年两地均不发生洪水,问在甲、乙两地怎样分配资金可获利最大? 试题详情
21.已知椭圆 试题详情

(1)求P点轨迹C的方程; 试题详情
(2)设A,B为曲线C上的两点,F(0, 试题详情
求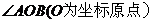 的最大值. 的最大值. 试题详情
文)已知函数f(x)=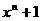  (1)讨论函数f(x)图象的对称性,并指出其一条对称轴或一个对称中心 试题详情
试题详情
试题详情
试题详情
试题详情
设 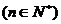 ,试问Tn是否存在最大值?若存在求出n的值; ,试问Tn是否存在最大值?若存在求出n的值; 若不存在,请说明理由?
试题详情
(文)已知椭圆 试题详情

(1)求P点轨迹C的方程; 试题详情
(2)设A,B为曲线C上的两点,F(0, 求 求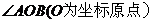 的最大值. 的最大值. 试题详情
一、选择题
B文(B)ACDB CACB(文A)B AD 二、填空题 13. 14.1200
15. (理)3(文)
14.1200
15. (理)3(文) 1
16.2 1
16.2 三、解答题 17. 解: ,且 ,且 . .   ① ………………3分 ① ………………3分
 ② ②


又A为三角形的内角,所以sinA= ………………6分 ………………6分 ………………9分 ………………12分 18.解:由题意p,q中有且仅有一个为真,一个为假,…………2分 由p真  m>2,……5分 m>2,……5分 q真 <0 <0 1<m<3, ……7分 1<m<3, ……7分 所以,若p假q真,则  1<m≤2……9分 1<m≤2……9分 若p真q假,则  m≥3……11分 m≥3……11分 综上所述:m∈(1,2)∪[3,+∞].…………12分 19.证明(1):过点D作  ,垂足为H.连结HB、GH, ,垂足为H.连结HB、GH,

所以 又 ,且 ,且 = = 所以 由三垂线定理得 …………(理、文)6分 …………(理、文)6分 (2)(理)  知 所以 连结DG,则 垂足G,所以 垂足G,所以 …………9分 …………9分 作 垂足为M,连结DM,则 垂足为M,连结DM,则 为二面角D-BF-C的平面角 为二面角D-BF-C的平面角 
所以,在 中, 中,  .…………12分 .…………12分 (注:也可用空间向量来解,步骤略) (文) 又∵AD∥面BFC 所以  = = = …………9分 …………9分   =0,得x= =0,得x=

所以x= 时 时 有最大值,其值为 有最大值,其值为 .…………12分 .…………12分 20.解:(1)由已知条件分析可知,在甲、乙两地分别投资5万元的情况下欲获利12.5万元,须且必须两地都不发生洪水. 故所求的概率为P=(1-0.6)×(1-0.5)=0.2………………(理)5分(文)6分 (2)设投资1万元在甲地获利 万元,则 万元,则 的可能取值为15万元和-5万元. 的可能取值为15万元和-5万元. 又此地发生洪水的概率为0.6 故投资1万元在甲地获利的期望为1.5×0.6+(-0.5)×0.4=0.7万元.…………(理)7分 同理在乙地获利的期望为1×0.5+(-0.2)×0.5=0.4万元. …………(理)8分 设在甲、乙两地的投资分别为x,y万元, 则平均获利z=0.7x+0.4y万元.……(理)9分  (则获得的利润z=1.5x+y万元.…………(文)7分) (则获得的利润z=1.5x+y万元.…………(文)7分)
其中x,y满足: 如右图,因为A点坐标为(6,4) 所以,在甲、乙两地的投资分别为6、4万元时, 可平均获利最大, 其最大值为(理)5.8万元、(文)13万元. …………(理、文)12分 (注:若不用线性规划的格式求解,只要结果正确同样给分) 21.解:(1)设平移后的右焦点为P(x,y), 易得已知椭圆的右焦点为F2(3,0),
………………1分 
(2)易知F(0, 为曲线C上的焦点,又 为曲线C上的焦点,又 所以A,B,F三点共线………………5分 设 
 ………………12分 ………………12分
(文)21.解:(1)当n为偶数时,因为f(-x)=(-x)n+1=xn+1=f(x),即函数f(x)为偶函数 所以其图象关于y轴对称………………2分 当n为奇数时,因为f(-x)=(-x)n+1=-xn+1,所以 所以其图象关于点(0,1)中心对称. ………………4分 (或:令g(x)=f(x)-1=xn,所以g(-x)=(-x)n=-xn=-g(x) ,即g(x)为奇函数, 所以g(x)的图象关于原点对称,故函数f(x)的图象关于点(0,1)中心对称.)………4分 (2) = = …………6分 …………6分 所以 …………# …………# 当 时 时 ;…………8分 ;…………8分 当 时,#式两边同乘以x,得 时,#式两边同乘以x,得 …* …* *式-#式可得, …………12分 …………12分 22.(理)解:(1)易得f(x)= + + 的定义域为[0,n] 的定义域为[0,n] 令 ,得x= ,得x= ------------1分 ------------1分 所以,函数f(x)在(0, )上单调递增,在( )上单调递增,在( ,n)单调递减, ,n)单调递减, 所以 = = ------------3分 ------------3分 由于 ,所以 ,所以 -------------5分 -------------5分 因为  , , 所以 --------8分 --------8分 (2)令 所以 = = ------------10分 ------------10分 由  ; ;

所以    -------------12分 -------------12分
又 ,所以 ,所以 相除得 ,由 ,由 得 得 ,所以 ,所以  
 最大
-----------14分 最大
-----------14分
| 
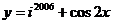 (其中
(其中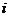 为虚数单位)的最大值和最小正周期分别是( )
为虚数单位)的最大值和最小正周期分别是( ) B 0,
B 0, 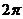 C
-2,
C
-2, 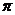 D
1,
D
1,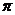
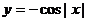 最小正周期是( )
最小正周期是( )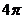 B
B 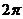 C
C 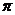 D
D 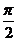
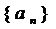 ( n
( n )满足
)满足 ,且
,且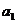 =-
=-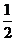 ,
, = ( ) A、
= ( ) A、 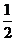 B、
B、
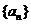 中,若
中,若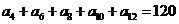 ,则其前15项的和为 ( )
,则其前15项的和为 ( ) 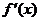 ,则f(1)+
,则f(1)+ 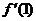 的值为 A. -2 B
的值为 A. -2 B 的解集为
的解集为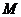 若
若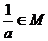 则a的取值范围
则a的取值范围