
2005学年海珠区九年级数学综合调研测试
选择题部分
一、选择题(本大题共10小题,每小题3分,共30分)
1、一元二次方程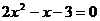 的一次项系数是
(
)
的一次项系数是
(
)
A. 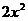 B. -
B. -
2、已知圆锥的侧面展开图的面积是 ,母线长是
,母线长是
A.
3、 化简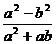 的结果是
(
)
的结果是
(
)
A.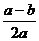 B.
B.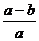 C.
C.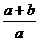 D.
D.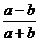
4、下列每张方格纸上都画有一个圆,只用不带刻度的直尺就能确定圆心位置的是
( )
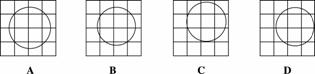
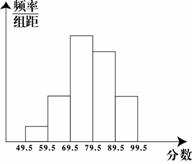 5、某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,现将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图(如右图),已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30那么在这次评比中被评为优秀的调查报告有
(
)
5、某校组织学生进行社会调查,并对学生的调查报告进行了评比,分数大于或等于80分为优秀,且分数为整数,现将某年级60篇学生调查报告的成绩进行整理,分成5组画出频率分布直方图(如右图),已知从左至右4个小组的频率分别是0.05,0.15,0.35,0.30那么在这次评比中被评为优秀的调查报告有
(
)
A、27篇 B、21篇 C、18篇 D、9篇
6、已知:一次函数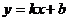 中,
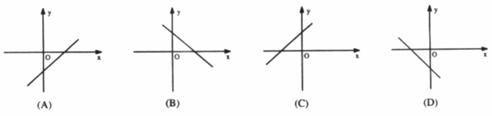
中,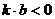 且y随x的增大而减小,则它的图象是
(
)
且y随x的增大而减小,则它的图象是
(
)
7、一张桌子上摆放着若干个碟子,从三个方向上看在眼里,三种视图如下图所示,则这张桌子上共有碟子为 ( )

(A)6个 (B)8个 (C)12个 (D)17个
8、若不等式组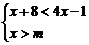 的解集是
的解集是 >3,则m的取值范围是 ( )
>3,则m的取值范围是 ( )
(A)m>3 (B)m≥3 (C) m<3 (D) m≤3
9、如图1,等边△ABC中,D是BC上的一点,△ABD经过旋转后到△ACE的位置,若
∠BAD=15度,那么旋转角是 ( )
 A、15度
B、45度
C、60度
D、35度
A、15度
B、45度
C、60度
D、35度
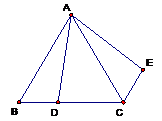
图1 图2
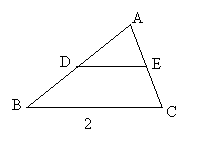
10、如图2,若DE是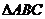 的中位线,则
的中位线,则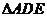 与四边形DECB的面积之比是
(
)
与四边形DECB的面积之比是
(
)
A.1∶2
B.1∶
非选择题部分(共120分)
二、填空题(本大题共6小题,每小题3分,共18分)
 11、函数y=
11、函数y=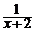 中,自变量x的取值范围是___________________;函数y=
中,自变量x的取值范围是___________________;函数y=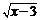 中,自变量x的取值范围是___________________。
中,自变量x的取值范围是___________________。
12、一串有黑有白,其排列有一定规律的珠子,被盒子遮住了一部分(如图),则这串珠子被盒子遮住的部分有_________粒。
 13、有一直角梯形零件ABCD,AD∥BC,斜腰DC的长为
13、有一直角梯形零件ABCD,AD∥BC,斜腰DC的长为
14、抛物线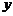 =-(
=-( +2)2-3的对称轴为直线________;顶点坐标为____________。
+2)2-3的对称轴为直线________;顶点坐标为____________。
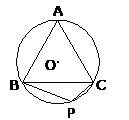
15、已知:如图,等边三角形ABC内接于⊙O,点P在 上,则
上,则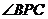 的度数为___________。
的度数为___________。
16、在Rt△ABC中,∠C=90°,AC=6,BC= 8,则其外接圆的半径为 。
三、解答题(本大题共9小题,满分102分)
17、(本大题满分9分)求不等式组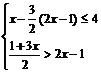 的整数解。
的整数解。
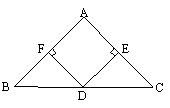 18、(本大题满分9分)已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,
18、(本大题满分9分)已知:如图,D是△ABC的BC边上的中点,DE⊥AC,DF⊥AB,
垂足分别是E、F,且BF=CE.求证:
(1)△ABC是等腰三角形;
(2)当∠A=90°时,试判断四边形AFDE是怎样的
四边形,证明你的结论。
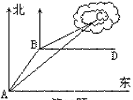 19、(本大题满分10分)一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
19、(本大题满分10分)一艘渔船在A处观测到东北方向有一小岛C,已知小岛C周围4.8海里范围内是水产养殖场.渔船沿北偏东30°方向航行10海里到达B处,在B处测得小岛C在北偏东60°方向,这时渔船改变航线向正东(即BD)方向航行,这艘渔船是否有进入养殖场的危险?
20、(本大题满分10分)如图,有两个可以自由转动的均匀转盘A、B,转盘A被均匀地分成4等分,每份分别标上1,2,3,4四个数字;转盘B被均匀地分成6等份,每份分别标上1,2,3,4,5,6六个数字。 有人为甲、乙两人设计了一个游戏,其规则如下:
(1)同时自由转动转盘A、B;
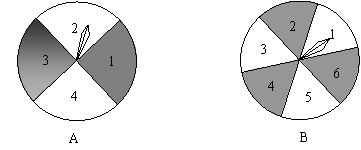 (2)转盘停止后,指针各指向一个
(2)转盘停止后,指针各指向一个
数字(如果指针恰好指在分格线上,那
么重转一次,直到指针指向某一数字为
止),用所指的两个数字作成积. 如果得
到的积是偶数,那么甲胜;如果得到的
积是奇数,则乙胜(如果转盘A指针指
向3,转盘B指针指向5,3×5=15,按
规则乙胜).
你认为这样的规则是否公平?请说
明理由;如果不公平,请你设计一个公平的规则,并说明理由.
21、(本大题满分12分)某产品每件成本是120元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间关系如下表:
x(元)
130
150
165
y(件)
70
50
35
若日销售量y是销售价x的一次函数,要获得最大销售利润,每件产品的销售价定为多少元?此时每日销售利润是多少?
22、(本大题满分12分)如果将点P绕定点M旋转180°后与点Q重合,那么称点P与点Q关于点M对称,定点M叫做对称中心。此时,M是线段PQ的中点。
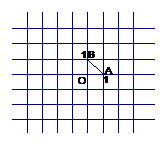 如图,在直角坐标系中,ㄓABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0)。点列P1、P2、P3、…中的相邻两点都关于ㄓABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…。对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环。已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标。
如图,在直角坐标系中,ㄓABO的顶点A、B、O的坐标分别为(1,0)、(0,1)、(0,0)。点列P1、P2、P3、…中的相邻两点都关于ㄓABO的一个顶点对称:点P1与点P2关于点A对称,点P2与点P3关于点B对称,点P3与P4关于点O对称,点P4与点P5关于点A对称,点P5与点P6关于点B对称,点P6与点P7关于点O对称,…。对称中心分别是A、B,O,A,B,O,…,且这些对称中心依次循环。已知点P1的坐标是(1,1),试求出点P2、P7、P100的坐标。
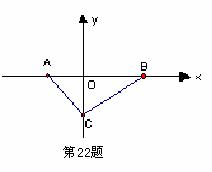 23、(本大题满分12分)如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C
23、(本大题满分12分)如图,在平面直角坐标系中,Rt△ABC的斜边AB在x轴上,顶点C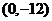 在y轴的负半轴上,tan∠ABC=
在y轴的负半轴上,tan∠ABC=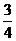 ,点P
,点P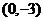 在线段OC上,
在线段OC上,
(1)求AP的长;
(2)在x轴上是否存在点Q,使以点A、C、P、Q为顶点的四边形是梯形?若存在,请直接写出直线PQ的解析式;若不存在,请说明理由.
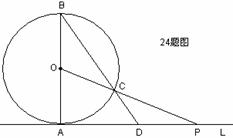 24、(本大题满分14分)如图,已知直线L与◎○相切于点A,直径AB=6,点P在L上移动,连接OP交◎○于点C,连接BC并延长BC交直线L于点D,
24、(本大题满分14分)如图,已知直线L与◎○相切于点A,直径AB=6,点P在L上移动,连接OP交◎○于点C,连接BC并延长BC交直线L于点D,
(1) 若AP=4, 求线段PC的长(5分)
(2) 若ΔPAO与ΔBAD相似,求∠APO
的度数和四边形OADC的面积(答
案要求保留根号)(9分)
25、(本大题满分14分)已知:如图,△ABC中,∠C=90°,AC=3厘米,CB=4厘米.两个动点P、Q分别从A、C两点同时按顺时针方向沿△ABC的边运动.当点Q运动到点A时,P、Q两点运动即停止.点P、Q的运动速度分别为1厘米/秒、2厘米/秒,设点P运动时间为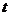 (秒).
(秒).
(1)当时间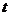 为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
为何值时,以P、C、Q三点为顶点的三角形的面积(图中的阴影部分)等于2厘米2;
(2)当点P、Q运动时,阴影部分的形状随之变化.设PQ与△ABC围成阴影部分面积为S(厘米2),求出S与时间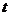 的函数关系式,并指出自变量
的函数关系式,并指出自变量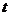 的取值范围;
的取值范围;
 (3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由。
(3)点P、Q在运动的过程中,阴影部分面积S有最大值吗?若有,请求出最大值;若没有,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com