
题目列表(包括答案和解析)
已知一次函数y=mx+4具有性质:y随x的增大而减小,又直线y=mx+4分别与直线x=1与x=4相交于点A、D,且点A在第一象限内,直线x=1,x=4分别与x轴相交于点B、C.
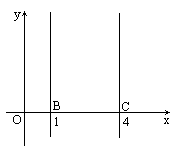
(1)要使四边形ABCD为凸四边形,求m的取值范围.
(2)已知四边形ABCD为凸四边形,直线y=mx+4与x轴相交于点E,当![]() =
=![]() 时,求这个一次函数的解析式.
时,求这个一次函数的解析式.
(3)在(2)条件下,设直线y=mx+4与y轴相交于点F,求证:D为EF的中点.
| kb |
| x |
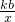 的图象在第二、四象限
的图象在第二、四象限| 某县决定鼓励农民开荒种植牡丹并实行政府补贴,规定每新种植一亩牡丹一次性补贴农户若干元经调查,种植亩数y(亩)与补贴数额x(元)之间成一次函数关系,且补贴与种植情况如下表: | ||||||||
(1)分别求出政府补贴政策实施后,种植亩数y(亩)、每亩牡丹的收益z(元)与政府补贴数额x(元)之间的函数关系式; (2)要使全县新种植的牡丹总收益W(元)最大,又要从政府的角度出发,政府应将每亩补贴数额x定为多少元?并求出总收益W的最大值和此时种植亩数;(总收益=每亩收益×亩数) (3)在(2)问中取得最大总收益的情况下,需占用其中不超过50亩的新种牡丹园,利用其树间空地种植新品种“黑桃皇后”已知引进该新品种平均每亩的费用为530元,此外还要购置其它设备,这项费用(元)等于种植面积(亩)的平方的25倍这样混种了“黑桃皇后”的这部分土地比原来种植单一品种牡丹时每亩的平均收益增加了2000元,这部分混种土地在扣除所有费用后总收益为85000元,求混种牡丹的土地有多少亩? |
| 补贴数额x(元) | 100 | 200 | … |
| 种植亩数y(亩) | 1600 | 2400 | … |
| 2 |
| 3 |
| 5 |
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com