1.2的倒数是          .

2．计算：(ab²)²=          .

3．右图是某物体的三视图，那么物体形状是          .

4．因式分解：2x²-8=          .

5．计算：          .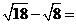

6．某班有7名同学参加校“综合素质智能竞赛”，成绩（单位：分）分别是87，92，87，89，91，88，76.则它们成绩的众数是      .分，中位数     .分.

7．已知圆椎的母线长为5cm，底面半径为3cm，则它的侧面积是    .cm²（结果可保留л）

8．用6个球（除颜色外没有区别）设计满足以下条件的游戏：摸到白球的概率为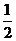，摸到红球的概率为，摸到黄球的概率为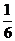.则应设    .个白球，   .个红球，  .个黄球.

9．在四边形ABCD中，AC是对角线.下列三个条件：①∠BAC=∠DAC；②BC=DC；③AB=AD.请将其中的两个作为已知条件，另一个作为结论构成一个真命题：如果                          那么             .

10．如右图，两个半径都是4cm的圆外切于点C，一只蚂蚁由点A开始依ABCDEFCGA的顺序沿着圆周上的8段长度相等的路径绕行，蚂蚁在这8段路径上不断地爬行，直到行走2006cm后才停下来.请问这只蚂蚁停在那一个点？答：停在    点.

11．下列各组数中，相等的是（     ）

A.(-1)³和1                 B.(-1)²和-1

C.|-1|和-1                 D.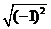和1

12．下列时间为必然事件的是（     ）

A.明天一定会下雨                    B.太阳从西边升起

C.5枚1元硬币分给4人，至少1个人得到2枚硬币

D.掷一个普通正方体骰子，掷的点数一定是6

13．将方程x+4x+1=0配方后，原方程变形为

A.(x+2)²=3                           B.(x+4)²=3

C.(x+2)²=-3                          D.(x+2)²=-5

14．在统计中，样本的标准差可以反映这组数据的（     ）

A.平均状态            B.分布规律    C.离散程度            D.数值大小

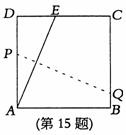
15．如图，将一块边长为12的正方形纸片ABCD的顶点A折叠至DC  边上的点E，使DE=5，这痕为PQ，则PQ的长为（    ）

A.12              B.13         C.14              D.15

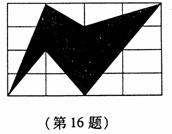
16．右图是某广告公司为某种商品设计的商标图案，若图中每个小长方形的面积都是1，则阴影部分的面积是（     ）

A.6             B.6.5        C.7           D.7.5

17.(7分)

化简：3（a+5b）-2(b-a)

18．（7分）

解不等式组：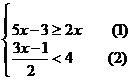

19．（8分）

解分式方程：

20．（8分）

请在下列王阁图中画出所给图形绕点O顺时针依次旋转90⁰、180⁰、270⁰后所成的图形（注意：有阴影部分图形旋转后的对应图形要涂上阴影.不要求写画法）

21．（8分）

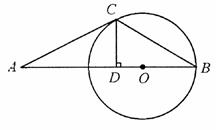
如图，B、C是⊙O上的点，线段AB经过圆心O 连结AC、BC，过点C作CD⊥AB于D, ∠ACD=2∠B.AC是O的切线吗？为什么？

22．（8分）

为了帮助贫困失学儿童，某团市委发起“爱心储蓄”          活动，鼓励学生将自己的压岁钱和零花钱存入银行，

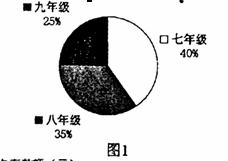
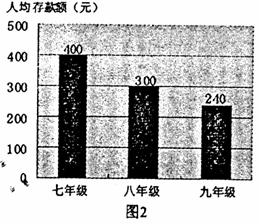
定期一年，到期后可取回本金，而把利息捐给贫困失学儿童.某中学共有学生1200人，图1是该校各年级学生人数比例分布的扇形统计图，图2是该校学生人均存款情况的条形统计图.

（1）九年级学生人均存款元；

（2）该校学生人均存款多少元？

（3）已知银行一年期定期存款的年利率是2.25% （“爱心储蓄”免收利息税），且每351元能提供 给一位失学儿童一学年的基本费用，那么该校一学年能帮助多少为贫困失学儿童. 23．（10分）

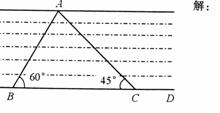
如图，为测河宽，小丽在河对岸岸边任意选取一点A，再在河这边B处观察A，此时视线BA与河岸BD所成的夹角为60⁰；小丽沿河岸BD向前走了50米到CA与河岸BD所成的夹角为45⁰.根据小丽提供的信息能测出河宽吗？若能，请写出求解过程；若不能，请说明理由.（结果精确到1米）

24．（12分）小明暑假到华东第一高峰-黄岗山（位于武夷山境内）旅游，导游提醒大家上山要多带一件衣服，并介绍当地山区气温会随海拔高度的增加而下降.沿途小明利用随身带的登山表（具有测定当前位置高度和气温等功能）测得以下数据：

海拔高度x米

400

500

600

700

…

气温y(⁰C）

28.6

28.0

27.4

26.8

…

（1）以海拔高度为x轴，气温为y轴，根据上表提供的数据在下列直角坐标系中描点；

（2）观察（1）中所苗点的位置关系，猜想y与x之间的函数关系，求出所猜想的函数表达式，并根据表中提供的数据验证你的猜想；

（3）如果小明到达山顶时，只告诉你山顶的气温为18.1，你能计算出黄岗山的海拔高度大约是多少米吗？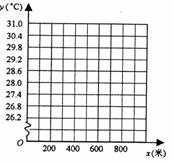

25．（14分）某公司2005年1-3月的月利润y（万元）与月份x之间的关系如图所示.图中的折线可近似看作是抛物线的一部分.

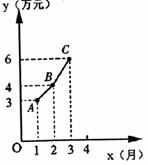
（1）根据图像提供的信息，求出过A、B、C三点的二次函数关系式；

（2）公司开展技术革新活动，定下目标：今年6月份的利润仍以图中抛物线的上升趋势上升.6月份公司预计将达到多少万元？

（3）如果公司1月份的利润率为13%，以后逐月增加1个百分点.已知6月上旬平均每日实际销售收入为3.6万元，照此推算6月份公司的利润是否会超过（2）中所确定的目标？

（成本总价=利润利润率，销售收入=成本总价+利润）

26．（14分）

定义：若某个图形可分割为若干个都与他相似的图形，则称这个图形是自相似图形. 探究：

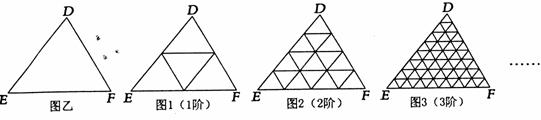
（1）如图甲，已知△ABC中∠C=90⁰，你能把△ABC分割成2个与它自己相似的小直角三角形吗？若能，请在图甲中画出分割线，并说明理由.

（2）一般地，“任意三角形都是自相似图形”，只要顺次连结三角形各边中点，则可将原三角形分割为四个都与它自己相似的小三角形.我们把△DEF(图乙)第一次顺次连结各边中点所进行的分割，称为1阶分割（如图1）；把1阶分割得出的4个三角形再分别顺次连结它的各边中点所进行的分割，称为2阶分割（如图2）…依次规则操作下去.n阶分割后得到的每一个小三角形都是全等三角形（n为正整数），设此时小三角形的面积为S_N.

①若△DEF的面积为10000，当n为何值时，2<S_n<3?

（请用计算器进行探索，要求至少写出三次的尝试估算过程）

②当n>1时，请写出一个反映S_n-1,S_n,S_n+1之间关系的等式（不必证明）