
2007年莘县中考模拟考试(一)
数学试题
注意事项:
1.试题分值150分。考试时间120分钟。
2.本试卷分试题和答卷两部分。答案直接写在答卷上,考试结束时只交答卷,不交试题部分。
一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一个选项符合题目要求)
1.在5,0.1,-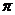 ,
,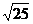 ,-
,-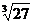 ,
,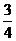 ,
,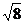 ,
,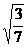 八个实数中,无理数有:
八个实数中,无理数有:
A.5个 B.4个 C.3个 D.2个
2.如图,

数轴上表示1, 的对应点分别为A、B,点B关于点A的对称点为点C,则点C表示的实数为:
的对应点分别为A、B,点B关于点A的对称点为点C,则点C表示的实数为:
A. -1
B.1-
-1
B.1- C.2-
C.2- D.
D. -2
-2
3.如图,是一个比例尺为l:100000000的我国地图,北京到佛山的图上距离是1.6cm,则北京、佛山两地之间的实际直线距离大约是:
A.1.8×103km B.1.8×10skm
C.1.6×103b D.1.6×106km
 (3题图)
(3题图)
4.如图,小明和爸爸、妈妈三个玩跷跷板.三人的体重一共为150千克,爸爸坐在跷跷板的一端,体重只有妈妈一半的小明和妈妈一同坐在跷跷板的另一端,这时爸爸那端仍然着地,那么小明的体重应小于:
A.49千克
B.50千克
C.24千克
D.25千克 
5.不改变分式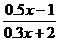 的值,把它的分子和分母中的各项系数都化为整数。所得的结果为:
的值,把它的分子和分母中的各项系数都化为整数。所得的结果为:
A.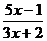 B.
B.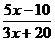 C.
C.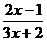 D.
D.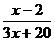
6.已知直线y=kx+b经过点Al(X1,y1)和A2(x2,y2),若k<0,且xl<X2,则y1与y2的大小关系是:
A.yl< y2 B.y1=y2 C.yl>y2 D.不确定
7.某青年排球队12名队员的年龄情况如右表所示,则这个队队员年龄的众数和中位数是:
年龄(岁)
18
19
20
2l
22
人数
l
4
3
2
2
A.19,20 B.19,19 C.19,20.5 D.20,19
8.设M表示直角三角形,N表示等腰三角形,P表示等边三角形,Q表示等腰直角三角形,则下列四个图中,能表示它们之间关系的是:
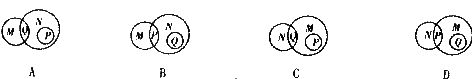
9.如图,一位篮球运动员站在罚球线上投篮,球入篮得分.下列图象中可以大致反映篮球出手后到入篮筐这一时间段内,篮球的高度h(米)与时间t(秒)之间的变化关系是:


10.如图,正方形硬纸片ABCD的边长是4,点E、F分别是AB、BC的中点,若把纸片沿左图中的虚线剪开,拼成右图的“小别墅”,则图中阴影部分的面积是:
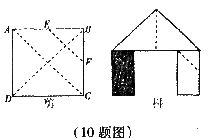
A.2 B.4 C.8 D.10
11.如图,有一等腰直角三角形纸片,以它的对称轴为折痕,将三角形对折,得到的三角形还是等腰直角三角形,仿照上述方法将原等腰直角三角形折叠四次,所得小等腰直角三角形的周长是原等腰直角三角形周长的:

A.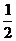 B.
B.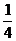 C.
C.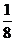 D.
D.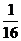

12.如图,⊙ A、⊙B、⊙C、⊙D相互外离,它们的半径都是1,顺次连结四个圆心得到四边形ABCD,则图中四个扇形(阴影部分)的面积之和为:
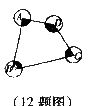
A.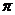 B.1.5
B.1.5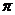 C.
2
C.
2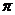 .
D.5
.
D.5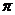
二、填空题(本题共5个小题。每小题4分,共20分.只要求填写最后结果)
13.若a,b都是无理数,且a+b=2,则a、b的值可以是:_______.(填上一组满足条件的值即可)
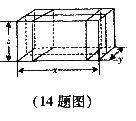
14.如图,要给这个长、宽、高分别为x、y、z的箱子打包,其打包方式如图所示,则打包带的长至少要____________.(用x、y、z的代数式表示)
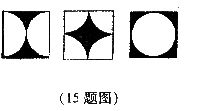
15.如图中的三个正方形边长都相等,其中的阴影部分面积相等吗?________.(填“相等”或“不相等”)
16.已知二次函数的图像开口向上,且顶点在y轴的负半轴上,请你写出一个满足条 件的二次函数的解析式__________.
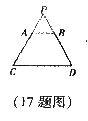
17.如图,电灯P在横杆AB的正上方,AB在灯光下的影子为CD,AB//CD,AB=2m,CD=5m,点P到CD的距离为3m,则点P到AB的距离为:________.
三、解答题(本题共8个小题'满分82分.解答应写出文字说明、证明过程或演算步骤)
18.(本题满分6分)如图,a、b、c是数轴上三个点A、B、C所对应的实数.

试化简: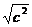 +|a-b|+
+|a-b|+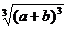 -|b+c|.
-|b+c|.
19.(本题满分6分)按下列程序计算,把答案填在表格内,然后看看有什么规律,想想为什么会有这个规律.
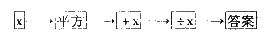
(1)填写表内空格:
输入x
3
2
-2

….
输出答案
….
(2)发现的规律是:_____________________.
(3)用简要的过程证明你发现的规律.
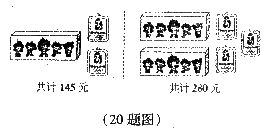
20.(本题满分10分)某商场正在热销2008年北京奥运会吉祥物“福娃”玩具和徽章两种奥运商品,根据图中提供的信息,求一盒“福娃”玩具和一枚徽章的价格.
21.(本题满分12分)如图,在网格中有一个四边形图案.
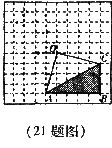
(1)请你分别画出此图案绕点O顺时针方向旋转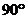 、
、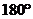 、
、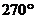 的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错噢;
的图案,你会得到一个美丽的图案,千万不要将阴影位置涂错噢;
(2)若网格中每个小正方形的边长为1,旋转后点A的对应点,依次为A1、A2、A3,求四边形AA1A2A3的面积;
(3)这个美丽图案能够说明一个著名结论的正确性,请写出这个结论.
22.(本题满分12分)某种汽车油箱可储油60升,加满油开始行驶,油箱中的剩余油量y(升)与行驶里程x(千米)之间的函数关系为一次函数,如图所示。

(1)求y与x的函数关系式;
(2)加满一箱汽油可以行驶多少千米?
23.(本题满分12分)某校课外活动小组对本校八年级500名学生进行了一次每周课余“上网”时间的抽样调查,结果如图所示(t为上网时间).
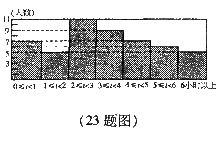
根据图中提供的信息,解答下列问题:
(1)本次抽样调查的学生人数是多少?
(2)每周上网时间在2≤t<3小时这组的频率是多少?
(3)每周上网时间的中位数落在哪个时间段?
(4)请估计该校八年级学生每周上网时问不少于4小时的人数.
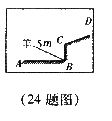
24.(本题满分12分)如图为一草地的平面图,ABCD为护栏,∠ABC=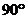 ,∠ BCD=
,∠ BCD=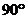 ,AB=6m,BC=3m,CD=8m.一根5m长的绳子,一端拴在柱子B上,另一端拴着一只羊(羊只能在草地上活动,不能越过护栏),请画出羊活动的最大区域,并求出其活动区域的面积.(保留精确值)
,AB=6m,BC=3m,CD=8m.一根5m长的绳子,一端拴在柱子B上,另一端拴着一只羊(羊只能在草地上活动,不能越过护栏),请画出羊活动的最大区域,并求出其活动区域的面积.(保留精确值)
25.(本题满分12分)某企业信息部进行市场调研发现:
信息一:如果单独投资A种产品,则所获利润yA。(万元)与投资金额X(万元)之间存在正比例函数关系:yA=kx,并且当投资5万元时,可获利润2万元.
信息二:如果单独投资B种产品,则所获利润yB。(万元)与投资金额X(万元)之间存在二次函数关系:yB=aX2+bx,并且当投资2万元时,可获利润2.4万元;当投资4万元时,可获利润3.2万元。
如果企业同时对A、B两种产品共投资10万元,请你设计一个能获得最大利润的投资方案,并求出按此方案能获得的最大利润.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com