1．在同一平面内，两条直线可能的位置关系是

    A．平行    B．相交    C．平行或相交    D．平行、相交或垂直

2．点到直线的距离是

A．点到直线上一点的连线  

B．点到直线的垂线

C．点到直线的垂线段       

D．点到直线的垂线段的长度

3．下列判断两角相等，方法错误的是

A．对顶角相等               

B. 两条直线被第三条直线所截，内错角相等

C．两直线平行，同位角相等   

D．∵∠1=∠2，∠2=∠3，∴∠1=∠3．

4．如图，点E在BC的延长线上，则下列条件中，不能判定AB∥CD的是

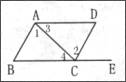
    A．∠3=∠4      B．∠B=∠DCE 

    C．∠l=∠2．    D．∠D+∠DAB=180°

5．下列图中，哪个可以通过左边图形平移得到

6．已知点A(-3，a)是点B(3，-4)关于原点的对称点，那么a的值的是

  A．-4         B．4         C．4或-4        D．不能确定

7．已知点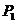 (-4，3)和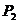(-4，-3)，则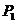和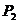

  A．关于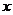轴对称  B．关于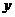轴对称  C．关于原点对称  D．不存在对称关系

8．在平面直角坐标系中，将三角形各点的纵坐标都减去3，横坐标保持不变，所得图形与原图形相比

  A．向右平移了3个单位    B．向左平移了3个单位

  C．向上平移了3个单位    D．向下平移了3个单位

9．点M(-7，0)在

  A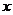．轴正半轴上  B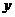．轴负半轴上  C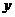．轴正半轴上   D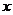．轴负半轴上

10．已知点P位于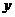轴右侧，距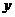轴3个单位长度，位于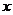轴上方，距离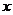轴4个单位长度，则点P坐标是

  A．(-3，4)    B．(3，4)    C．(-4，3)     D．(4，3)

11．将下列长度的三条线段首尾顺次相接，能组成三角形的是

  A．4cm 3cm 5cm   B．1cm 2cm 3cm   C．25cm l2cm 11cm   D．2cm 2cm 4cm

12．用一批完全相同的多边形地砖铺地面，不能进行镶嵌的是

  A、正三角形    B、正方形    C、正八边形    D、正六边形

13．已知线段a、b、c，有a>b>c，则组成三角形必须满足的条件是

  A．a+b>c    B．b+c>a    C．c+a>b     D．a-b>c

14．能把三角形的面积平分的是

  A．三角形的角平分线      B．三角形的高

  C．三角形的中线          D．以上都不对

15．如图，直线EF分别交CD、AB于M、N，且∠EMD=65°，∠MNB=115°，则下列结论正确的是

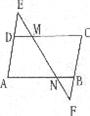
A．∠A=∠C    B．∠E=∠F    C．AE∥FC    D．AB∥DC

第Ⅱ卷  综合分析题(共12小题 总分75分)

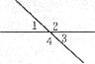
16．如图，已知两直线相交，∠1=30°则∠2=        ，∠3=         ，∠4=           

17．如果两个角是对顶角，且互补，则这两个角的大小为     ____    .

18．命题“同角的补角相等”的题设是               ，结论是                   ．

19．三角形的两边的长分别为2cm和7cm，若第三边的长为奇数，则三角形的周长是      ．

20．在△ABC中，∠A：∠B：∠C=2：3：4，则∠B=             .

21．如图，EF∥AD，∠l=∠2，∠BAC=70°．将求∠AGD的过程填写完整．(8分)

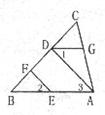
解：  因为EF∥AD，

    所以∠2=        (                    )．

    又因为∠l=∠2，

    所以∠l=∠3(                        )，

    所以AB∥          (                         )，

    所以∠BAC+            =180°(                             )．

    因为∠BAC=70°，

    所以∠AGD=           .

22．在图所示的平面直角坐标系中表示下面各点   (10分)

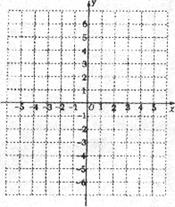
    A(0，3)，      B(1，-3)，   C(3，-5)，

    D(-3，-5)，    E(3，5)，    F(5，7)。

   (1)A点到原点O的距是                              。

   (2)将点C向轴的负方向平移6个单位，它与点         重合。

   (3)连接CE，则直线CE与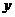轴是什么关系?

   (4)点F分别到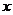、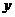轴的距离是多少?

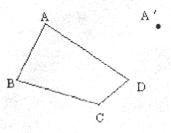
23．如图：将四边形ABCD进行平移后，使点A的对应点为点A′，请你画出平移后所得的四边形A′B′C′D′(画图工具不限，只作图即可)。(5分)

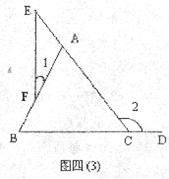
24．如图四(3)，E是△ABC的边CA延长线上一点，F是AB上一点，D点在BC的延长线上，试说明： ∠1<∠2。(6分)

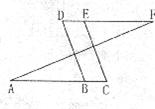
25．如图，已知DF∥AC，∠C=∠D，你能否判断CE∥BD?试说明你的理由(8分)

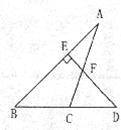
26．)如图，△ABC中，D在BC的延长线上，过D作DE⊥AB于E，交AC于F.已知∠A=30°，∠FCD=80°，求∠D．(8分

27．有趣玩一玩：中国象棋中的马颇有骑士风度，自古有“马踏八方”之说，如图六(1)，按中国象棋中“马”的行棋规则，图中的马下一步有A、B、C、D、E、F、G、H八种不同选择，它的走法就象一步从“日”字形长方形的对角线的一个端点到另一个端点，不能多也不能少。

    要将图六(2)中的马走到指定的位置P处，即从(四，6)走到(六，4)，现提供一种走法：

(四，6)→(六，5) →(四，4) →(五，2) →(六，4) (10分)

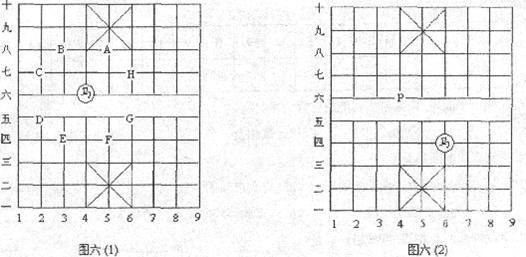
(1)下面是提供的另一走法，请你填上其中所缺的一步：

(四，6) →(五，8) →(七，7) →             →(六，4)。

(2)请你再给出另两种走法(只要与前面的两种走法不完全相同即可，步数不限)。