
2007年延庆县初三升学模拟考试(一)
数 学 试 卷
第Ⅰ卷 (选择题32分)
考生须知
1.第Ⅰ卷为选择题,只有一道大题,共2页。答题前要认真审题,看清题目要求,按要求认真作答。
2.第Ⅰ卷各题均须按规定要求在“机读答题卡”上作答,题号要对应,填涂要规范。
3.考试结束后,考生应将试卷和“机读答题卡”一并交监考老师收回。
一、 选择题(共8个小题,每小题4分,共32分)
1. 3的相反数是
3的相反数是
A3
B. C.
C. 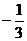 D
D 3
3
2.蜜蜂建造的蜂房即坚固又省料,蜂房的巢壁厚约为0.000073米 , 用科学记数法表示为
A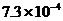 米 B.
米 B. 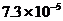 米
米
C.  米
D
米
D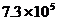 米
米
 3.如图,直线
3.如图,直线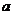 与直线
与直线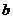 互相平行,则
互相平行,则 的值是
的值是
A.20 B.80
C.120 D.180
4.
如图,在 中,
中,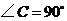 ,
,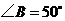 ,
, ,则
,则 的长为
的长为
 A.
A. B.
B.
C.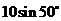 D.
D.
5.估算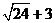 的值( )
的值( )
A.在5和6之间 B.在6和7之间
C.在7和8之间 D.在8和9之间
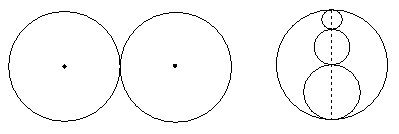
6. 某公园计划砌一个形状如图(1)所示的喷水池,后来有人建议改为图(2)的形状,且外圆的直径不变,喷水池边沿的宽度、高度不变,你认为砌喷水池的边沿
A.图(1)需要的材料多 B.图(2)需要的材料多
 C.图(1)、图(2)需要的材料一样多 D.无法确定
C.图(1)、图(2)需要的材料一样多 D.无法确定


图(1) 图(2)
7. 在全国 “创建文明城市”综合评比中,某市各项综合指标名次如图:

则图中五个数据的众数和平均数依次是
A、32,36 B、45,32 C、36,45 D、45,36
8.如图,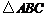 中,
中, ,
,
 将
将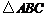 绕顶点
绕顶点 旋转
旋转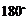 ,点
,点 落在
落在
 处,则
处,则 的长为
的长为
A. B.
B.
C.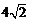 D.4
D.4
2007年延庆县初三升学模拟考试(一)
数 学 试 卷
第Ⅱ卷 (非机读卷88分)
考生须知
1.考生认真填写密封线内的区(县)名、学校名、姓名、报名号、准考证号。
2.第Ⅱ卷包括五道大题,共8页。答题前要认真审题,看清题目要求,按要求认真作答。
3.答题时字迹要工整,画图要清晰,卷面要整洁。
4.除画图可以用铅笔外,答题必须用黑色或蓝色钢笔、圆珠笔。
题号
二
三
四
五
总分
得分
阅卷人
复查人
二.填空题(共4小题,每小题4分,共16分)
9. 在函数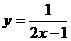 中, 自变量
中, 自变量 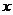 的取值范围是
.
的取值范围是
.
10.对于实数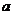 、
、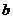 定义一种新运算“
定义一种新运算“ ”:
”: 则
则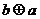 。
。
11.小红、小明、小芳在一起做游戏时,需要确定游戏的先后顺序.他们约定用“剪子、包袱、锤子”的方式确定.问在一个回合中三个人都出包袱的概率是____________
12.如图,依次连结第一个正方形各边的中点得到第二个正方形,再依次连结第二个正方形各边的中点得到第三个正方形,按此方法继续下去.若第一个正方形边长为1,则第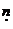 个正方形的面积是_________________.
个正方形的面积是_________________.

三、(共6个小题,每小题5分,共30分)
13. 请你从下列各式,任选两式作差,并将得到的式子进行因式分解.
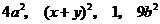
14. 已知: 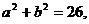
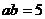 ,求
,求 的值.
的值.
15. 解不等式组 :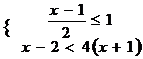 ,并写出不等式组的正整数解.
,并写出不等式组的正整数解.
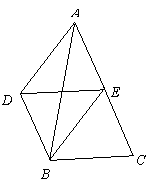 16. 如图,
16. 如图,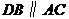 ,且
,且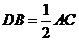 ,
,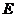 是
是 的中点,
的中点,
求证: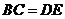 .
.
17. 解方程: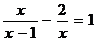
18. 如图, 在梯形ABCD 中, AD∥BC, AB = CD = AD,∠B = 60°,E 是AD上一点(不与A、D重合), F 在AB上,且AE = BF,DF、CE交于点P。
⑴ 请你判断 CE 与 DF的大小关系,并加以证明;
⑵ 试确定∠EPF的度数(直接写出结果)

四、(共4个小题,每小题5分,共20分)
 19.如图,点
19.如图,点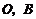 坐标分别为
坐标分别为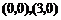 ,将
,将 绕
绕 点按逆时针方向旋转
点按逆时针方向旋转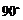 到
到 .
.
(1)画出 ;
;
(2)点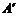 的坐标为 ;
的坐标为 ;
(3)求 的长.
的长.
20.已知关于一元二次方程 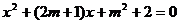 有两个不相等的实数根,试判断直线
有两个不相等的实数根,试判断直线  能否通过点A(-3,5),并说明理由 .
能否通过点A(-3,5),并说明理由 .
21. 有两个可以自由转动的均匀转盘 ,分别被分成4等份,3等份,并在每份内均标有数字,如图所示,丁洋和王倩同学用这两个转盘做游戏,游戏规则如下:
,分别被分成4等份,3等份,并在每份内均标有数字,如图所示,丁洋和王倩同学用这两个转盘做游戏,游戏规则如下:
 ①分别转动转盘
①分别转动转盘 和
和 ;②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止);③如果和为0,丁洋获胜,否则王倩获胜.
;②两个转盘停止后,将两个指针所指份内的数字相加(如果指针恰好停在等分线上,那么重转一次,直到指针指向某一份为止);③如果和为0,丁洋获胜,否则王倩获胜.
(1)用列表法(或树状图)求丁洋获胜的概率;
(2)你认为这个游戏对双方公平吗?请说明理由.
22.如图,A、B是⊙O的直径,BC是⊙O的弦, OD⊥BC于的E,交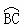 于点D.
于点D.
(1)请写出三个不同类型的正确结论;
(2)连接CD,设∠CDB = α,∠ABC = β,试找出α与β之间的一种关系式,并给予证明.

五、(共3个小题,共22分)
23(本题满分7分)
如图,已知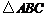 的面积为3,且
的面积为3,且 ,现将
,现将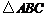 沿
沿 方向平移
方向平移 长度得到
长度得到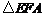 .
.
(1)求 所扫过的图形的面积;
所扫过的图形的面积;
(2)试判断 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
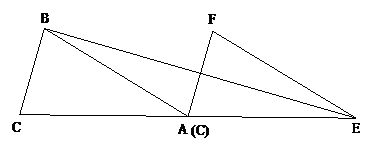 (3)若
(3)若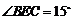 ,求
,求 的长.
的长.
24.(本题满分7分)
在数学学习过程中,通常是利用已有的知识与经验,通过对研究对象进行观察、实验、推理、抽象概括,发现数学规律,揭示研究对象的本质特征.
比如“同底数幂的乘法法则”的学习过程是利用有理数的乘方概念和乘法结合律,由“特殊”到“一般”进行抽象概括的: ,
, ,
, ,……
,……  , ∴
, ∴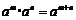 (
(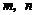 都是正整数).
都是正整数).
我们亦知: ,
,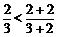 ,
,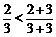 ,
, ,
, .
.
(1)请你根据上面的材料归纳出 之间的一个数学关系式;
之间的一个数学关系式;
(2)试用(1)中你归纳的数学关系式,解释下面生活中的一个现象:“若 克糖水里含有
克糖水里含有 克糖,再加入
克糖,再加入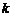 克糖(仍不饱和),则糖水更甜了”;
克糖(仍不饱和),则糖水更甜了”;
(3)如图,在 中,
中,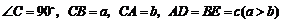 .能否根据这个图形提炼出与(1)中同样的关系式?并给予证明.
.能否根据这个图形提炼出与(1)中同样的关系式?并给予证明.
 |
25.(本题满分8分)
如图,已知二次函数图象的顶点坐标为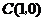 ,直线
,直线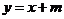 与该二次函数的图象交于
与该二次函数的图象交于 、
、 两点,其中
两点,其中 点的坐标为
点的坐标为 ,
, 点在
点在 轴上.
轴上.
(1)求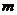 的值及这个二次函数的关系式;
的值及这个二次函数的关系式;
(2)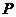 为线段
为线段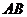 上的一个动点(点
上的一个动点(点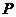 与
与 ,
, 不重合),过
不重合),过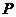 作
作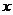 轴的垂线与这个二次函数的图象交于
轴的垂线与这个二次函数的图象交于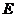 点,设线段
点,设线段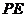 的长为
的长为 ,点
,点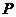 的横坐标为
的横坐标为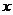 ,求
,求 与
与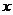 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量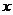 的取值范围;
的取值范围;
 (3)
(3) 为直线
为直线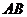 与这个二次函数图象对称轴的交点,在线段
与这个二次函数图象对称轴的交点,在线段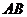 上是否存在一点
上是否存在一点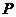 ,使得四边形
,使得四边形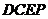 是平行四边形?若存在,请求出此时
是平行四边形?若存在,请求出此时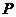 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com