
2008年绍兴市高三教学质量调测
理科综合能力测试
本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷1至2页,第Ⅱ卷3至10页。满分150分。考试结束后,将本试题卷和答题卡一并交回。
第Ⅰ卷 (选择题 共50分)
注意事项:
1. 本科考试分试题卷和答题卷,考生须在答题卷上作答,答题前,请在答题卷的密封线内填写学校、班级、学号、姓名;
2. 本试卷分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共6页,全卷满分150分,考试时间120分钟。
参考公式:
如果事件A、B互斥,那么P(A+B)=P(A)+P(B).
如果事件A、B相互独立,那么P(A?B)=P(A)?P(B).
如果事件A在一次试验中发生的概率是P,那么它在n次独立重复试验中恰好发生k次
的概率
球的表面积公式 ,其中R表示球半径。
,其中R表示球半径。
球的表体积公式 ,其中R表示球半径。
,其中R表示球半径。
一、选择题(本大题共10小题,每小题5分,共50分。在每小题给出的四个选项中,只有一项符合题目要求的)
1. 若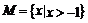 ,则下列选项中正确的是
,则下列选项中正确的是
A.
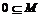 B.
B. 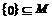 C.
C.
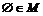 D.
D.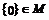
2. 设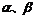 为两个平面,
为两个平面,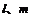 为两条直线,且
为两条直线,且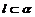 ,
,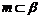 ,有如下两个命题:①若
,有如下两个命题:①若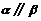 ,则
,则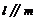 ;②若
;②若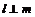 ,则
,则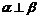 ,那么
,那么
A. ①是真命题,②是假命题 B. ①是真命题,②是假命题
C. ①是真命题,②是真命题 D. ①是假命题,②是假命题
3. 已知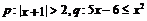 ,则
,则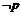 是
是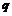 的
的
A. 充分不必要重要条件 B. 必要不充分条件
C. 充要条件下 D. 既不充分又不必要条件
4. 下列各选项中,与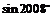 最接近的数是
最接近的数是
A.
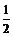 B.
B.
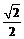 C.
C.
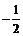 D.
D.
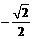
5. 某学校共在2008名学生,将从中选项派5名学生在某天去国家大剧院参加音乐晚会,若采用以下方法选取:先用简单随机抽样从2008名学生中剔除8名学生,再从2000名学生中随机抽取5名,则其中学生甲被选取的概率是
A.
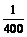 B.
B.
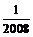 C.
C.
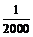 D.
D.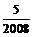
6. 在等差数列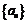 中,若
中,若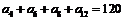 ,则
,则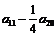 的值为
的值为
A.
18
B.
7. 设是离散型随机变量,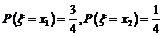 ,又已知
,又已知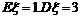 ,且
,且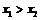 ,则
,则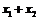 的值是
的值是
A.
4
B. 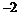
8. 已知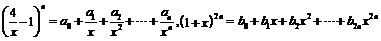 ,
,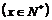 。记
。记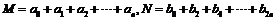 ,则
,则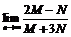 的值是
的值是
A.
2 B. 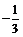 C. 0 D.
C. 0 D. 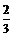
9.  一圆形纸片的圆心为O,点Q是圆内异于O点的一定点,点A是圆周上一点,把纸征折叠使点A与点Q重合,然后展平纸片,折痕CD与OA交于P点,当点A运动时点P的轨迹是
一圆形纸片的圆心为O,点Q是圆内异于O点的一定点,点A是圆周上一点,把纸征折叠使点A与点Q重合,然后展平纸片,折痕CD与OA交于P点,当点A运动时点P的轨迹是
A. 椭圆
B. 双曲线
C. 抛物线
D. 圆
10.已知实数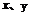 满足
满足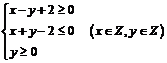 ,每一对整数
,每一对整数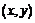 对应平面上一个点,则过这些点中的其中三点可作多少个不同的圆
对应平面上一个点,则过这些点中的其中三点可作多少个不同的圆
A.70
B.
第Ⅱ卷 (非选择题 共100分)
二、填空题 (本题共有7小题,每小题4分,共28分)
11.已知复数z满足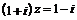 ,则z=
。
,则z=
。
12.若函数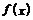 的反函数
的反函数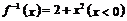 ,则
,则 。
。
13.已知角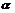 的终边在射线
的终边在射线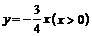 上,则
上,则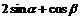 的值是
。
的值是
。
14.如果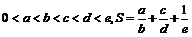 ,则把变量
(填入
,则把变量
(填入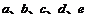 中的某个字母)的值增加1会使S的值增加最大。
中的某个字母)的值增加1会使S的值增加最大。
15.已知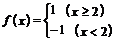 ,则不等式
,则不等式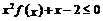 的解集是
。
的解集是
。
16.已知M是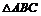 内的一点,且
内的一点,且 。定义:
。定义: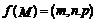 ,其中
,其中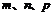 分别为
分别为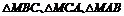 面积,若
面积,若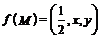 ,则
,则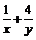 的最小值是 。
的最小值是 。
 17.如图,对于函数
17.如图,对于函数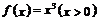 上任意两点
上任意两点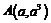 ,
,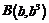 线段AB在弧线段AB的上方,
线段AB在弧线段AB的上方,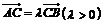 则由图中点C在
则由图中点C在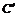 上方可得不等式
上方可得不等式 ,请分析函数
,请分析函数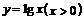 的图象,类比上述不等式可以得到的不等式是
。
的图象,类比上述不等式可以得到的不等式是
。
三、解答题(本大题共5小题,共72分,解答应写出文字说明、证明过程或演算过程)
18.(本小题满分14分)
在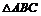 中,
中,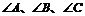 所对的边分别为
所对的边分别为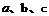 。若
。若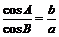 且
且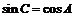
(1) 求角A、B、C的大小;
(2) 设函数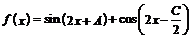 ,求函数
,求函数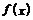 的单调递增区间,并指出它相邻两对称轴间的距离。
的单调递增区间,并指出它相邻两对称轴间的距离。
19.(本小题满分14分)
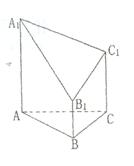
如图,已知五面体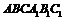 中
中 ,且
,且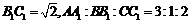 ,又
,又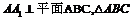 ,是边长为1的正三角形
,是边长为1的正三角形
(1) 问在线段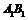 上是否存在一点M,使得
上是否存在一点M,使得 ,若存在,求出
,若存在,求出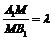 的值,若不存在,说明理由;
的值,若不存在,说明理由;
(2) 求二面角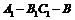 的大小。
的大小。
20.(本小题满分14分)
双曲线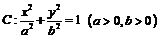 的离心率为2,且
的离心率为2,且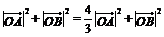 ,其中O为坐标原点,
,其中O为坐标原点,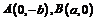
(1) 求双曲线C的方程;
(2)
设直线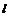 过右焦点
过右焦点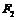 有与双曲线C的右支交于P,Q两点,无论直线
有与双曲线C的右支交于P,Q两点,无论直线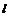 绕点
绕点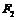 怎样转动,在
怎样转动,在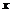 轴上总存在一个定点
轴上总存在一个定点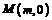 ,使
,使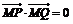 恒成立,求实数
恒成立,求实数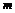 的值。
的值。
21.(本小题满分15分)
函数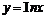 关于直线
关于直线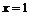 对称的函数为
对称的函数为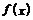 ,又函数
,又函数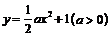 的导函数为
的导函数为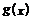 ,记
,记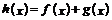
(1) 设曲线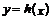 在点
在点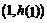 处的切线为
处的切线为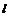 ,若
,若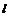 与圆
与圆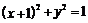 相切,求
相切,求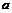 的值;
的值;
(2) 求函数 的单调区间;
的单调区间;
(3) 求函数 在[0,1]上的最大值;
在[0,1]上的最大值;
22.(本小题满分15分)
已知数列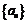 中的各项均为正数,且满足
中的各项均为正数,且满足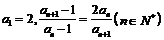 。记
。记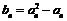 ,数列
,数列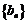 的前
的前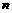 项和为
项和为 ,且
,且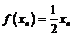
(1) 求数列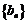 和
和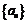 的通项公式;
的通项公式;
(2) 求证: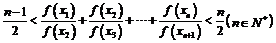




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com