
2007-2008学年度东北育才中学第一学期期末考试试卷
八年级数学试题
考试时间:120分钟 试卷满分:100分
一、选择题(每小题2分,计20分)
1、 的算术平方根是( )
的算术平方根是( )
(A) (B)2 (C)
(B)2 (C)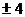 (D)4
(D)4
2、点A( ,
, )在( )
)在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
3、函数 中自变量
中自变量 的取值范围是( )
的取值范围是( )
(A) (B)
(B) 且
且 (C)
(C) (D)
(D) 且
且
4、二元一次方程组 的解也是二元一次方程
的解也是二元一次方程 的解,则
的解,则 的值为:
的值为:
(A) (B)
(B)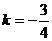 (C)
(C) (D)
(D)
5、如图:把边长为AD=

(A)
6、如图:直角梯形ABCD中,AD∥BC,AB⊥BC,AD=2,BC=3,将腰CD以D为中心逆时针旋转90°至ED,连接AE、CE,则△ADE的面积是( )
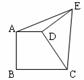
(A)1 (B)2 (C)3 (D)以上都不对
7、如图:在□ABCD 中,AB BC,AE、CF分别为∠BAD、∠BCD的平分线,连接BD,分别交AE、CF于点G、H,则图中的全等三角形共有( )
BC,AE、CF分别为∠BAD、∠BCD的平分线,连接BD,分别交AE、CF于点G、H,则图中的全等三角形共有( )
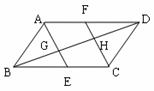
(A)3对 (B)4对 (C)5对 (D)6对
8、在平面直角坐标系中,设点P到原点的距离为m,OP与 轴的正方向的夹角为
轴的正方向的夹角为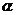 ,则用
,则用 表示点P的极坐标,显然,点P的坐标和它的极坐标存在一一对应的关系,例如点P的坐标(1,1)的极坐标为P(
表示点P的极坐标,显然,点P的坐标和它的极坐标存在一一对应的关系,例如点P的坐标(1,1)的极坐标为P(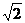 ,
, ),则极坐标Q(
),则极坐标Q(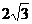 ,
, )的坐标为( )
)的坐标为( )
(A) (B)
(B) (C)
(C)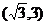 (D)
(D)
9、下面命题:(1)无理数都是无限小数; (2)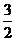 ,2,
,2, 是勾股数; (3)一次函数
是勾股数; (3)一次函数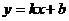 的图像不经过第二象限,则
的图像不经过第二象限,则 >0,
>0, <0; (4)对角线互相垂直且相等的四边形是正方形; (5)若
<0; (4)对角线互相垂直且相等的四边形是正方形; (5)若 、
、 …
… 的平均数为
的平均数为 ,则
,则 ,
, ,…
,… 的平均数为
的平均数为 其中正确的命题有( )
其中正确的命题有( )
(A)1个 (B)2个 (C)3个 (D)4个
10、已知直线 上有一点B(1,n),它到原点的距离为
上有一点B(1,n),它到原点的距离为 ,则该直线与两坐标轴围成的三角形面积为( )
,则该直线与两坐标轴围成的三角形面积为( )
(A) (B)
(B)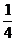 或
或  (C)
(C)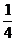 或
或 (D)
(D) 或
或
二 填空题(每小题3分,计30分)
11、若一个数的平方根等于它的立方根,则这个数是
12、已知 是
是 的整数部分,
的整数部分, 是
是 的小数部分,则
的小数部分,则
 =
=
13、将直线 向右平移1个单位长度后所得直线的解析式为
向右平移1个单位长度后所得直线的解析式为
14、某省男子篮球队在一次联赛中,共进行了十场比赛,得分如下(单位:分):
97,91,85, ,91,84,86,85,82,88,已知平均得分为88分,则
,91,84,86,85,82,88,已知平均得分为88分,则 众数为
中位数为
众数为
中位数为
15、已知A、C两点坐标分别为( )和(1,1),平行四边形ABCD的一个内角为30°,点B在x轴上,则点B的坐标为
)和(1,1),平行四边形ABCD的一个内角为30°,点B在x轴上,则点B的坐标为
16、将两张宽度相等的矩形叠放在一起得到如图所示的四边形 ,则四边形
,则四边形 是 形,若两张矩形纸片的长都是10,宽都是4,那么四边形
是 形,若两张矩形纸片的长都是10,宽都是4,那么四边形 周长的最大值=
周长的最大值=

17、如图:直线 与
与 轴交于点A,与直线
轴交于点A,与直线 交于点B,且直线
交于点B,且直线 与
与 轴交于点C,则△ABC的面积为
轴交于点C,则△ABC的面积为



18、如图:菱形ABCD中,AB=2,∠BAD=60°,E为AB的中点,P为对角线AC上的一个动点,则PE+PB的最小值为
19、如图:有一种动画程序,屏幕上正方形ABCD是黑色区域(含正方形边界),其中A( )、B(
)、B( )、C(
)、C(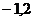 )、D(
)、D(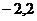 ),用信号枪沿直线
),用信号枪沿直线 发射信号,当信号遇到黑色区域时,区域便由黑色变为白色,则能使黑色区域变白的b的取值范围是
发射信号,当信号遇到黑色区域时,区域便由黑色变为白色,则能使黑色区域变白的b的取值范围是
20、不论 为何值时,一次函数
为何值时,一次函数 的图象恒过一定点,则这个定点坐标为
的图象恒过一定点,则这个定点坐标为
三、解答题(共计40分)
21、(4分)计算: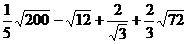
22、(5分)解方程组 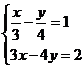
23、(7分)某种洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续的过程,其中进水、清洗、排水时洗衣机中的水量 (L)与时间
(L)与时间 (min)之间的关系如折线图所示,根据图像解答下列问题:
(min)之间的关系如折线图所示,根据图像解答下列问题:


(1)洗衣机进水时间是多少分钟?清洗衣物时洗衣机中的水是多少升?
(2)已知洗衣机的排水速度为每分钟
①求排水时 与
与 的函数关系式。
的函数关系式。
②如果排水时间为2min,求排水结束时洗衣机中剩下的水量。
24、(8分)如图:是规格为8×8的正方形的网格,请你在所给的网格中按下列要求操作:
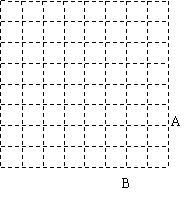

(1)请在网格中建立直角坐标系,使A点坐标为(4, ),B点坐标为(2,
),B点坐标为(2, )
)
(2)在第四象限的格点上,画一点C,使点C与线段组成一个以AB为底的等腰三角形,且腰长为无理数,则C点坐标是 ,△ABC的周长是
(3)画出△ABC以点C为旋转中心,旋转180°后的△A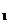 B
B C,连接AB
C,连接AB 和A
和A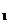 B,试写出四边形AB A
B,试写出四边形AB A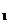 B
B 是何特殊四边形,并说明理由。
是何特殊四边形,并说明理由。
25、(8分)如图①,在正方形ABCD中,P是对角线AC上一点,PE⊥AB,PF⊥BC垂足分别为,E、F,
(1)请你猜想EF和PD有何关系,并证明
(2)如图②若点P是对角线AC延长线上任意一点,其它条件不变,请根据已知补全图形,并判断(1)中你所猜想的结论还成立吗?(不需要证明)

26、(8分)2006年多哈亚运会组委会公布的足球四分之一决赛门票价格(合人民币)是,一等席300元,二等席200元,三等席125元,某运动服装公司在促销活动中,组织获得特等奖、一等奖的共36名顾客到卡塔尔的多哈观看足球四分之一决赛,除去其他费用后,计划买两种门票用完5025元,你能设计几种购票方案,供该公司选择?并说明理由。
27、(10分)如图:已知直线 经过点A
经过点A 、点B
、点B ,交
,交 轴于点M
轴于点M
(1)求 的值及AM的长
的值及AM的长
(2)在 轴的负半轴上确定点P,使得△AMP成等腰三角形,请你直接写出点P的坐标。
轴的负半轴上确定点P,使得△AMP成等腰三角形,请你直接写出点P的坐标。
(3)将直线AB绕点A逆时针旋转45°得到直线AC,点D(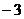 ,b)在AC上,连接BD,设BE是△ABD的高,过点E的射线EF将△ABD的面积分成2:3两部分,交△ABD的另一边于点F,求点F的坐标。
,b)在AC上,连接BD,设BE是△ABD的高,过点E的射线EF将△ABD的面积分成2:3两部分,交△ABD的另一边于点F,求点F的坐标。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com