
2007-2008学年度济宁微山县第一学期期中考试
八年级数学试题
注意事项:
1.本试题分第Ⅰ卷和第Ⅱ卷两部分,共12页。第Ⅰ卷第1页至第4页为选择题,36分;第Ⅱ卷第5页至第12页为非选择题,84分;共120分。考试时间为100分钟。
2.答卷前务必将自己的姓名、考号等填写在装订线内规定位置。
第Ⅰ卷 (选择题 共36分)
一、选择题(本大题共12小题,每小题3分,共36分。在每小题给出的四个选项中,只有一个是正确的。每小题选对得3分,选错、不选或多选,均不得分,并把答案填写在第Ⅱ卷的答题栏内。)
1.下列函数①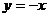 ;②
;②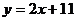 ;③
;③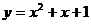 ;④
;④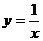 中,是一次函数的有
中,是一次函数的有
A.4个 B.3个 C.2个 D.1个
2.直线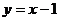 与两坐标轴分别交于A、B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有
与两坐标轴分别交于A、B两点,点C在坐标轴上,若△ABC为等腰三角形,则满足条件的点C最多有
A.4个 B.5个 C.7个 D.8个
3.图1是水滴进玻璃容器的示意图(滴水速度不变),图2是容器中水的高度随滴水时间变化的图像。
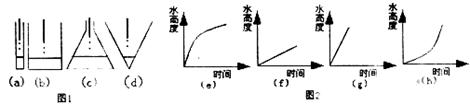
给出下列对应:
(1):(a)―(e) (2):(b)―(f) (3):(c)―(h) (4):(d)―(g)
其中正确的是
A.(1)和(2) B.(2)和(3)
C.(1)和(3) D.(3)和(4)
4.下列图形中(图3),一次函数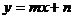 与正比例函数
与正比例函数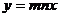 ,(m、n为常数且mn≠0)的图像大致是
,(m、n为常数且mn≠0)的图像大致是

5.如图4,是某单位职工年龄的频数分布直方图(统计中采用“上限不在内”的原则,如年龄为36岁统计在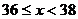 小组,而不在
小组,而不在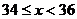 小组),根据图形提供的信息,指出下列说法错误的是
小组),根据图形提供的信息,指出下列说法错误的是

A.年龄在36≤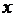 <38小组的频数是6
<38小组的频数是6
B.年龄在40≤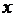 <42小组的人数占该单位总人数的20%
<42小组的人数占该单位总人数的20%
C.年龄为39岁的人数一定最多
D.年龄小于40岁的职工有21人
6.要清楚地表明一病人的体温变化情况,应选择的统计图是
A.扇形统计图 B.条形统计图 C.折线统计图 D.直方图
7.在对n个数据整理的频率分布表中,各组的频数之和与频率之和分别为
A.1,n B.1,
8.“阳光体育”运动在我市轰轰烈烈开展,为了解同学们最喜爱的阳光体育运动项目,小王对本班50名同学进行了跳绳,羽毛球,篮球,乒乓球,踢毽子等运动项目最喜爱人数的调查,并根据调查结果绘制了如图5的人数分布直方图,若将其转化为扇形统计图,那么最喜爱打篮球的人数所在扇形区域的圆心角的度数为
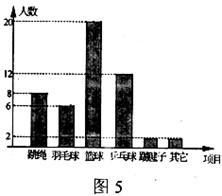
A.120º B.144º C.180º D.72º
9.下列说法:①用一张像底冲洗出来的2张1寸相片是全等形;②所有的正三角形都是全等形;③全等三角形的周长相等;④面积相等的三角形一定是全等三角形。其中正确的是
A.①③ B.①③④ C.①②③ D.③
10.如图6:AB=AC,BE⊥AE 于E,CF⊥AB于F,BE、CF相交于点D,则
①△ABE≌△ACF;②△BDF≌△CDE;③点D在∠A的平分线上。
以上结论中正确的是
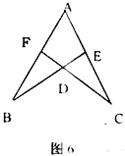
A.只有① B.只有② C.只有①和② D.①②③
11.如图7,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分为三个三角形,则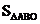 ∶
∶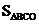 ∶
∶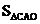 等于
等于
A.1∶1∶1 B.1∶2∶
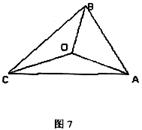
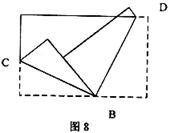
12.将一张长方形纸片按如图8所示的方式折叠,BC,BD为折痕,则∠CBD的度数为
A.60º B.75º C.90º D.95º
第Ⅱ卷(非选择题,共84分)
二、填空题(本大题共6小题,每小题3分,共18分。只要求填出最后结果。)
13.已知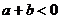 ,
,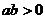 ,则一次函数
,则一次函数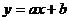 不经过第 象限。
不经过第 象限。
14.已知直线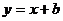 与坐标轴围成的三角形面积是2,则此直线的函数解析式是
。
与坐标轴围成的三角形面积是2,则此直线的函数解析式是
。
15.把一组64个数据的样本分成8组,从第一组到第四组的频数分别为5、7、11、13,第五组到第七组的频率都是0.125,则第八组的频率为 。
16.厂家为了宣传某种品牌的彩电几年的出厂价在逐年降低,你认为厂家用 统计图来表示数据最恰当。
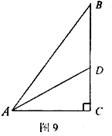
17.如图9,△ABC中,∠C=90º,AD平分∠BAC,AB=5,CD=2,则△ABD的面积是 。

18.如图10,是小华用半透明的纸糊的四边形的风筝,他糊好后用手边的量角器测量一下发现,无论支架AB与CD有多长,只要满足DA=DB,CA=CB,那么∠CAD与∠CBD总是相等的,则其中的道理是 。
三、解答题(共66分,解答应写出文字说明、证明过程或推演步骤)
19.(本题满分8分)
已知一次函数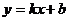 的图像经过点A(-2,-3)及点B(1,6)。
的图像经过点A(-2,-3)及点B(1,6)。
(1)求此一次函数的解析式,并画出函数图像。
(2)求此函数图像与坐标轴围成的三角形的面积。
20.(本题满分8分)
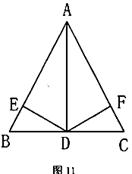
如图11,在△ABC中,D是BC的中点,DE⊥AB于E,DF⊥AC于点F,且BE=CF。
求证:AD平分∠BAC。
21.(本题满分9分)
实验中学对初二年级女生仰卧起坐的测试成绩进行统计分析,将数据整理后,画出频数分布直方图,如图12,已知图中从左到右的第一、第二、第三、第四、第六小组的频率依次是0.10,0.15,0.20,0.30,0.05,第五小组的频数是36,根据所给的图填空:
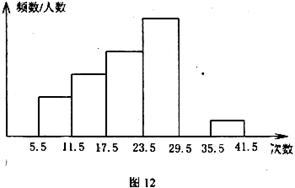
(1)第五小组的频率是 ,请补全这个频数分布图。
(2)参加这次测试的女生人数是 ;若次数在24(含24次)以上为达标(此标准为中考体育标准),则该校初二年级女生的达标率为 。
(3)请你用统计知识,以中考体育标准对微山县所有中学初二女生仰卧起坐成绩的达标率作一个估计。
22.(本题满分9分)图13是某班学生外出乘车、步行、骑车的人数分布直方图和扇形分布图。
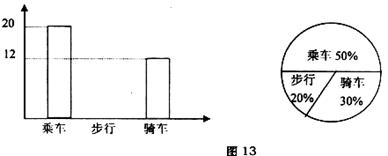
(1)该班有多少名学生?
(2)补上步行分布直方图的空缺部分;
(3)在扇形统计图中,求骑车人数所占的圆心角度数。
23.(本题满分10分)
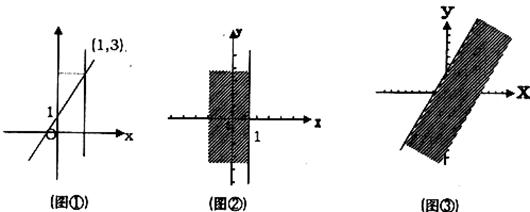
观察图①可以解出,直线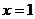 与直线
与直线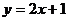 的交点P的坐标(1,3),就是方程组
的交点P的坐标(1,3),就是方程组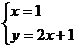 的解,所以这个方程组的解为
的解,所以这个方程组的解为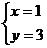 。
。
在直角坐标系中,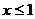 表示一个平面区域,即直线
表示一个平面区域,即直线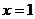 以及它左侧的部分,如图②;
以及它左侧的部分,如图②;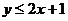 也表示一个平面区域,即直线
也表示一个平面区域,即直线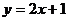 以及它下方的部分,如图③。
以及它下方的部分,如图③。
回答下列问题:
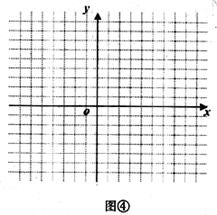
(1)在直角巫标系(图④)中,用作图像的方法求出方程组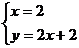 的解;
的解;
(2)用阴影表示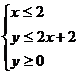 所围成的区域,并求阴影部分的面积。
所围成的区域,并求阴影部分的面积。
24.(本题满分10分)

25.(本题满分12分)
实验中学欲利用星期日派七、八、九年级的学生共80人去某公园参加植树活动,共完成700棵的植树任务(每个年级都要参加)。已知七年级学生每人每天植树8棵,可获取报酬22元;八年级学生每人每天植树10棵,可获取报酬26元;九年级学生每人每天植树12棵,可获取报酬28元。
设其中派去参加植树活动的七年级学生有 名,八年级学生
名,八年级学生 名。
名。
(1)试写出 、
、 所满足的二元方程,并用含
所满足的二元方程,并用含 的代数式表示
的代数式表示 即参加植树活动的八年级学生的人数;
即参加植树活动的八年级学生的人数;
(2)如果实验中学获取的报酬总额为w元,求w与 之间的函数关系式;并求出自变量
之间的函数关系式;并求出自变量 的取值范围;
的取值范围;
(3)学校若想以获取最少的报酬完成植树任务,请你为实验中学设计分派学生的方案。此方案学校获取的最少报酬是多少?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com