
2008年贵阳市中考模拟试卷七
数学
一、填空题(每小题3分,共30分)
1.因式分解: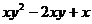 =
.
=
.
2.我们知道,1纳米=10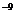 米,一种花粉直径为35000纳米,那么这种花粉的直径用科学记数法可记为
米.
米,一种花粉直径为35000纳米,那么这种花粉的直径用科学记数法可记为
米.
3.计算: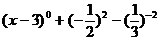 =
.
=
.
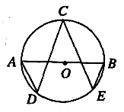
4.如下图,AB是⊙O的直径,点C、D、E都在⊙O上,若∠C=∠D=∠E,则∠A+∠B=
.
5.某体育训练小组有2名女生和3名男生,现从中任选1人去参加学校组织的“我为奥运添光彩”志愿者活动,则选中女生的概率为
6.某移动公司为了调查手机发送短信的情况,在本区域的1000位用户中抽取了10位用户来统计他们某月份发送短信息的条数,结果如下表所示,则这组数据的中位数是 ,众数是 .
手机用户序号
1
2
3
4
5
6
7
8
9
10
发送短信息条数
85
78
83
79
84
85
86
88
80
85
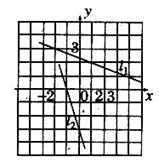
7.如下图,是在同一坐标系内作出的一次函数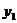 、
、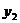 的图像
的图像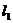 、
、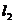 ,设
,设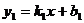 ,
,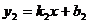 ,则
,则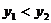 的
的 的取值范围是
.
的取值范围是
.
8.反比例函数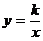 的图像如下图所示,点M是该函数图像上一点,MN垂直于
的图像如下图所示,点M是该函数图像上一点,MN垂直于 轴,垂足是点N,如果S△MON=2,则k的值为 .
轴,垂足是点N,如果S△MON=2,则k的值为 .
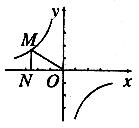
9.如下图,在△ABC中,AB=AC=5,BC=6,点E、F是中线AD上的两点,则图中阴影部分的面积是 .
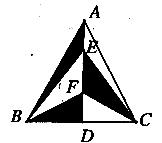
10.李老师在与同学进行“蚂蚁怎样爬最近”的课题研究时设计了以下一个题:如图(1),圆锥的母线长为4cm,圆锥的侧面展开图如图(2)所示,且∠AOA1=120°,一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.根据所给的条件,可求出蚂蚁需要爬行的最短路程的长度是 .
二、选择题(以下每小题都有A、B、C、D四个选项。其中只有一个选项正确,请把正确选项的字母选入该题的括号内,每小题4分,共20分)
11.不等式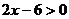 的解集在数轴上表示正确的是( ).
的解集在数轴上表示正确的是( ).

12.一物体及其主视图如下图所示,则它的左视图与俯视图分别是右侧图形中的( ).
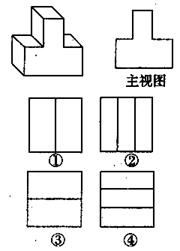
A.①② B.③② C.①④ D.③④
13.在下列命题中,正确的是( ).
A.一组对边平行的四边形是平行四边形
B.有一个角是直角的四边形是矩形
C.有一组邻边相等的平行四边形是菱形
D.对角线互相垂直平分的四边形是正方形
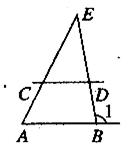
14.如下图,AB∥CD,∠1=110°,∠ECD=70°,∠E的大小是 ( ).
A.30° B.40° C.50° D.60°
15.沈阳市的春天经常刮风,给人们的出行带来很多不便,小明观测了4月6日的连续12 个小时的风力变化情况,并画出了风力随时间变化的图像(如图),则下列说法正确的是( ).

A.在8时至14时,风力不断增大 B.8时风力最小
C.在8时至12时,风力最大为7级 D.20时风力最小
三、解答题
16.(本题7分)
请在下面集合(1)中选2个单项式,在集合(2)中选2个实数,再用“+,一,×,÷”四个运算符号中的两个和等号连接成一个方程使其解为正整数.并求出方程的解.

17.(本题12分)
已知二次函数 的图像如下图所示,它与
的图像如下图所示,它与 轴相交于点C,点D在二次函数图像上与点C对称,一次函数的图像过点A、D;
轴相交于点C,点D在二次函数图像上与点C对称,一次函数的图像过点A、D;
(1)求点D的坐标;(4分)
(2)求一次函数的解析式;(6分)
(3)写出二次函数的值大于一次函数的值的 的取值范围.(2分)
的取值范围.(2分)

18.(本题7分)
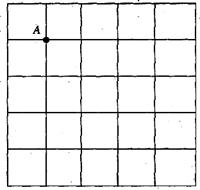
如下图,在5×5的正方形网格中,每个小正方形的边长都为1,请在所给网格中按下列要求画出图形.
(1)从点A出发的一条线段AB,使它的另一个端点落在格点(即小正方形的顶点)上,且长度为2 ;(3分)
;(3分)
(2)以(1)中的AB为边的一个等腰△ABC,使点C在格点上,且另两边的长都是无理数.(4分)。
19.(本题10分)
如下图,某风景区的湖心岛有一凉亭A,其正东方向有一棵大树B,小明想测量A、B之间的距离,他从湖边的C处测得A在北偏西45°方向上,测得B在北偏东32°方向上,且量得B、C之间的距离为100米,根据上述测量结果,请你帮小明计算A、B之间的距离是多少?(结果精确到1米).

20.(本题12分)
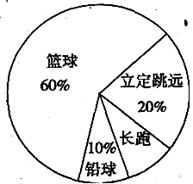
光明中学七年级1班同学积极响应“阳光体育工程”的号召,利用课外活动时间积极参加体育锻炼.每位同学从长跑、篮球、铅球、立定跳远中选一项进行训练,训练前后都进行了测试.现将项目选择情况及训练后篮球定时定点投篮测试成绩整理后作出如下统计图表.请你根据图表中的信息回答下列问题:
(1)选择长跑训练的人数占全班人数的百分比是 ,该班共有同学 人;(4分)
(2)求训练后篮球定时定点投篮人均进球数;(4分)
(3)根据测试资料,训练后篮球定时定点投篮的人均进球数比训练之前人均进球数增加25%.请你求出参加训练之前的人均进球数. (4分)
训练后篮球定时定点投篮测试进球数统计表
进球数(个)
8
7
6
5
4
3
人数
2
1
4
7
8
2
21.(本题12分)
某工厂计划招聘A、B两个工种的工人120人,已知A、B两个工种的工人的月工资分别为800元和1000元.
(1)若工厂每月所支付的工资为110000元,那么A、B两个工种的工人各招聘多少人?(4分)
(2)若要求B工种的人数不少于A工种人数的2倍,那么招聘A工种的工人多少人时,可使每月所支付的工资最少.(8分)
22.(本题12分)
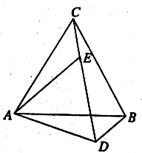
已知:如下图,△ABC和△ADE都是等边三角形,点E在CD上.
(1)求证:BD=CE;(5分)
(2)求∠CDB的度数;(3分)
(3)图中是否存在通过旋转能够互相重合的两个三角形.若存在,请说明旋转过程;若不存在,请说明理由.(4分)
23.(本题8分)
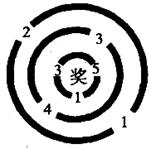
如下图,某学校七年级数学兴趣小组组织一次数学活动.在一座有三道环形路的数字迷宫的每个进口处都标记着一个数,要求进入者把自己当做数“1”,进入时必须乘进口处的数,并将结果带到下一个进口,依次累乘下去,在通过最后一个进口时,只有乘积是5的倍数,才可以进入迷宫中心,现让一名5岁小朋友小军从最外环任一个进口进入.
(1)小军能进入迷宫中心的概率是多少?请画出树状图进行说明.(4分)
(2)小组两位组员小张和小李商量做一个小游戏,以猜测小军进迷宫的结果比胜负.游戏规则规定:小军如果能进入迷宫中心,小张和小李各得1分;小军如果不能进入迷宫中心,则他在最后一个进口处所得乘积是奇数时,小张得3分,所得乘积是偶数时,小李得3分,你认为这个游戏公平吗?如果公平,请说明理由;如果不公平,请在第二道环进口处的两个数中改变其中一个数使游戏公平.(4分)
24.(本题10分)
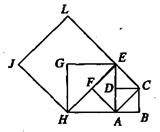
如下图,正方形ABCD的面积是1,以对角线AC为边作第二个正方形ACEF,再以对角线AE为边作第三个正方形AEGH,如此作下去……
(1)记正方形ABCD边长为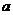 ,按上述方法所作正方形的边长依次为
,按上述方法所作正方形的边长依次为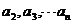 ,求
,求 ;(4分)
;(4分)
(2)求 ;(4分)
;(4分)
(3)当n=10时,求第十个正方形的面积.(2分)
25.(本题10分)
某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件,后来经过市场调查,发现这种商品单价每件降低1元,其销量可增加10件.
(1)求商场经营该商品原来一天可获利润多少元?(2分)
(2)设后来该商品每件降价 元,商场一天可获利润
元,商场一天可获利润 元.
元.
①若商场经营该商品原来一天可获利润2160元,则每件商品应降价多少元?(4分)
②求出 与
与 之间的函数关系式,当
之间的函数关系式,当 为多少时,商场可获得最大利润?并画出该函数图像的草图,观察其图像的变化趋势,结合题意写出当
为多少时,商场可获得最大利润?并画出该函数图像的草图,观察其图像的变化趋势,结合题意写出当 取何值时,商场获利润不少于2160元?(4分)
取何值时,商场获利润不少于2160元?(4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com