
2008年广东省汕头市潮南区中考模拟试卷
数 学
一、选择题(在答题卡上填涂,本大题共8小题,每小题4分,共32分):
1.下列计算正确的是( )
A.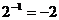 ; B.
; B.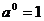 ; C.
; C.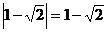 ; D.
; D.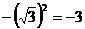
2.下列多项式能用平方差公式分解因式的是( )
A.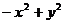 ; B.
; B.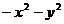 ; C.
; C.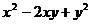 ; D.
; D.
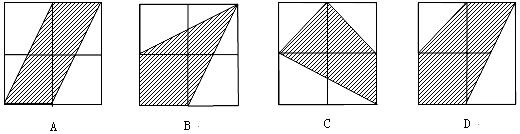
3.下列各图中,每个正方形网格都是由四个边长为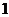 的小正方形组成,其中阴影部分面积为
的小正方形组成,其中阴影部分面积为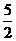 的是( )
的是( )
4.下图是由一些相同的小正方体构成的几何体的三视图,在这个几何体中,小正方体的个数是( )

A.7; B.6; C.5; D.4
5.将点P(2, )向上平移2个单位长度,再绕坐标系原点O旋转180º,得到点Q,则点Q的坐标为( )
)向上平移2个单位长度,再绕坐标系原点O旋转180º,得到点Q,则点Q的坐标为( )
A. ; B.
; B. ; C.
; C.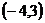 ; D.
; D.
6.下列图形不能折成正方体的是( )

A. B. C. D.
7.把一个半径为
A.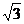 cm; B.
cm; B. cm; C.
cm; C. cm; D.
cm; D.
8.规定※是一种新的运算符号,且 ※
※ =
= ,例如:2※3=2×3+2+3=11,
,例如:2※3=2×3+2+3=11,
那么(3※4)※1=( )
A.19; B.29; C.39; D.49
二、填空题(把答案直接写在答卷的相应位置,本大题共5小题,每小题4分,共20分):
9.如图,若平行四边形ABCD与平行四边形EBCF关于直线BC对称,∠DCF=100º,
则∠A=________.(填度数)

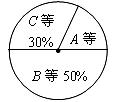
10..据统计,某班50名学生参加2008年初中毕业生学业考试,综合评价等级为A、B、C等的学生情况如扇形图所示,则该班得A等的学生约有 名.
11.请写出不等式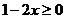 的一个无理数解:___________________.
的一个无理数解:___________________.
12.如图,一根电线杆的接线柱部分AB在阳光下的投影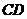 的长为
的长为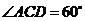 ,则
,则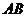 的长为
m.(精确到
的长为
m.(精确到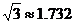 )
)
13.标准田径场跑道的周长为
三、解答题(在答卷上解答,本大题共5小题,每小题7分,共35分):
14.解不等式组: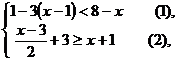 并在数轴上表示出其解集。
并在数轴上表示出其解集。
15. 已知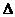 ABC位于平面直角坐标系内如图。
ABC位于平面直角坐标系内如图。
(1)将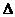 ABC各顶点的坐标分别乘以
ABC各顶点的坐标分别乘以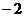 ,作为点A1、B1、C1的坐标,画出
,作为点A1、B1、C1的坐标,画出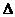 A1B
A1B
(2)指出通过怎样的几何变换可以由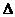 A1B
A1B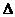 ABC?
ABC?
16.在一个不透明的口袋中装有红、白、黑三种颜色的小球若干个,它们只有颜色不同,其中有白球2个,黑球1个,已知从中任意摸出1个球得白球的概率为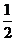 .
.
(1)求口袋中有多少个红球;
(2)求从袋中一次摸出2个球,得一红一白的概率,要求画出树状图.
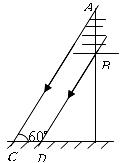
17.课外实践活动中,数学老师带领学生测量学校旗杆的高度.如图,在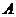 处用测角仪(离地高度为
处用测角仪(离地高度为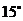 ,朝旗杆方向前进
,朝旗杆方向前进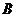 处,再次测得旗杆顶端的仰角为
处,再次测得旗杆顶端的仰角为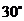 ,求旗杆
,求旗杆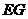 的高度.
的高度.
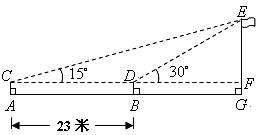
18.某校高中一年级组建篮球队,对甲、乙两名备选同学进行定位投篮测试,每次投10个球,共投10次.甲、乙两名同学测试情况如图所示:
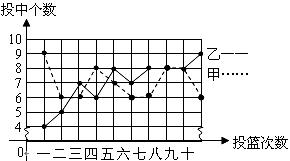
(1)根据图中所提供的信息填写下表:
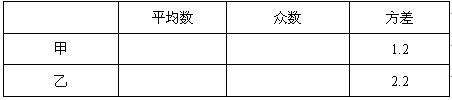
(2)如果你是高一学生会文体委员,会选择哪名同学进入篮球队?请说明理由.
四、(在答卷上解答,本大题共3小题,每小题9分,共27分):
19.(1)在同一平面直角坐标系中作出反比例函数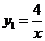 与一次函数
与一次函数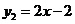 的图像,并根据图像求出交点坐标.(要求列对应值表,6分)
的图像,并根据图像求出交点坐标.(要求列对应值表,6分)
(2)观察图像,当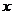 取任何值时,
取任何值时,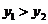 ?(3分)
?(3分)
20.李明家和陈刚家都从甲、乙两供水点购买同样的一种桶装矿泉水,李明家第一季度从甲、乙两供水点分别购买了10桶和6桶,共花费51元;陈刚家第一季度从甲、乙两供水点分别购买了8桶和12桶,且在乙供水点比在甲供水点多花18元钱。若只考虑价格因素,通过计算说明到哪家供水点购买这种桶装矿泉水更便宜一些?
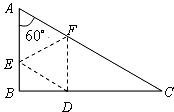
21.如图,在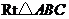 中,∠B=90°
中,∠B=90°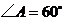 ,点
,点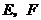 分别在
分别在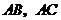 上,沿
上,沿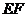 对折,使点
对折,使点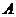 落在
落在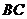 上的点
上的点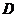 处,且
处,且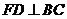 .求证:四边形
.求证:四边形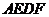 是菱形.
是菱形.
五、(在答卷上解答,本大题共3小题,每小题12分,共36分):
22.某产品每件成本10元,试销阶段每件产品的销售价x(元)与产品的日销售量y(件)之间的关系如下表:
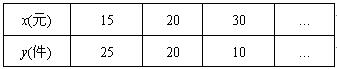
若日销售量y是销售价x的一次函数.
(1)求出日销售量y(件)与销售价x(元)的函数关系式;
(2)要使每日销售利润最大,每件产品的销售价应定为多少元?此时,每日销售的利润是多少元?
23.如图,ΔABC中,AC=BC,以BC上一点O为圆心、OB为半径作⊙O交AB于点D。已知经过点D的⊙O切线恰好经过点C。
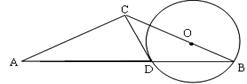
(1)试判断CD与AC的位置关系,并证明。(5分)
(2)若ΔACB∽ΔCDB,且AC=3,求圆心O到直线AB的距离。
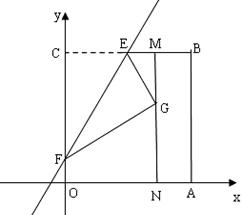
24.如图,四边形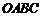 是一张放在平面直角坐标系中的正方形纸片.点
是一张放在平面直角坐标系中的正方形纸片.点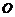 与坐标原点重合,点
与坐标原点重合,点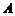 在
在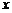 轴上,点
轴上,点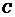 在
在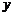 轴上,
轴上,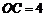 ,点
,点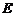 为
为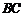 的中点,点
的中点,点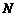 的坐标为
的坐标为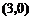 ,过点
,过点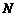 且平行于
且平行于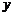 轴的直线
轴的直线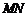 与
与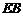 交于点
交于点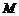 .现将纸片折叠,使顶点
.现将纸片折叠,使顶点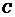 落在
落在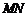 上,并与
上,并与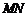 上的点
上的点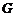 重合,折痕为
重合,折痕为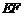 ,点
,点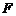 为折痕与
为折痕与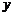 轴的交点.
轴的交点.
(1)求∠EGM的度数;
(2)求折痕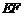 所在直线的解析式;
所在直线的解析式;
(3)设点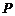 为直线
为直线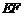 上的点,是否存在这样的点
上的点,是否存在这样的点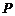 ,使得以
,使得以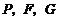 为顶点的三角形为等腰三角形,若存在,请直接写出点
为顶点的三角形为等腰三角形,若存在,请直接写出点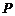 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com