
2009年北京市石景山区初三第一次统一练习暨毕业考试
数学试卷
一、选择题(共8个小题,每小题4分,共32分)
1.27的立方根是
A.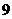 B.
B.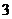 C.
C.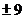 D.
D.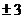
2.北京奥组委和国际奥委会在新闻发布上说:“中国有8亿4千万(840000000)人观看了奥运会开幕式,这确实是一个令人惊讶的数字.” 840000000这个数字用科学记数法可表示为
A.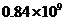 B.
B.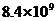 C.
C.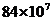 D.
D.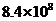
3.如果两圆半径分别为3和4,圆心距为6,那么这两圆的位置关系是
A.相交 B.内切 C.外离 D.外切
4.在一个暗箱里,装有3个红球、5个黄球和7个绿球,它们除颜色外都相同,搅拌均匀后,从中任意摸出一个球是红球的概率是
A.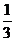 B.
B.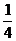 C.
C.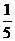 D.
D.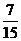
5.要使式子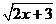 有意义,字母
有意义,字母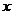 的取值必须满足
的取值必须满足
A.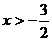 B.
B.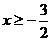 C.
C.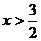 D.
D.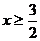
6.某校初三(1)班一组女生体重数据统计表如下:
体重(千克)
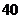
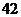
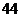
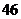
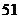
人数(人)
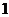
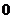
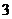
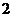
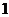
该组女生体重的平均数、众数、中位数分别是
A.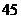 、
、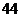 、
、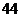 B.
B.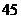 、
、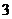 、
、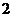 C.
C.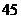 、
、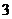 、
、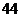 D.
D.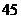 、
、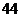 、
、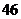
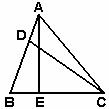
7.已知:如下图,在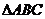 中,
中,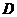 是
是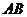 边上的一点,且
边上的一点,且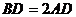 ,
,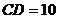 ,
, 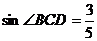 ,则
,则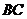 边上的高
边上的高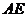 的长为
的长为
A.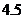 B.
B.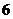 C.
C.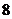 D.
D.
8.若正方形网格中的每个小正方形的边长都是1,则把每个小格的顶点叫做格点.现有一个表面积为12的正方体,沿着一些棱将它剪开,展成以格点为顶点的平面图形,下列四个图形中,能满足题意的是
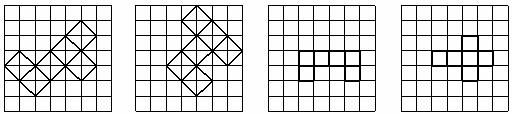
A B C D
二、填空题(共4个小题,每小题4分,共16分)
9.分解因式: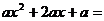 .
.
10.若关于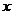 的方程
的方程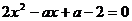 有两个相等的实根,则
有两个相等的实根,则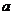 的值是 .
的值是 .
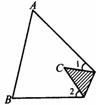
11.三角形纸片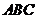 中,
中,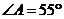 ,
,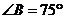 ,将纸片的一角折叠,使点
,将纸片的一角折叠,使点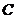 落在
落在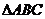 内(如下图),则
内(如下图),则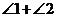 =_________°.
=_________°.
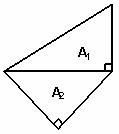
12.将一副三角板如图放置,则上下两块三角板面积之比 :
: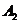 等于________.
等于________.
三、解答题(共5个小题,每小题5分,共25分)
13.计算: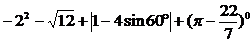 .
.
14.解不等式组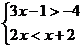 ,并把它的解集表示在数轴上.
,并把它的解集表示在数轴上.
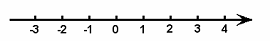
15.解方程: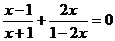 .
.
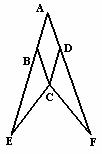
16.已知:如下图,在菱形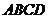 中,分别延长
中,分别延长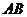 、
、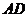 到
到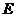 、
、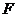 ,使得
,使得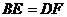 ,联结
,联结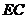 、
、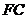 .
.
求证: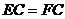 .
.
17.已知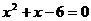 ,求代数式
,求代数式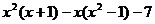 的值.
的值.
四、解答题(共2个小题,每小题5分,共10分)
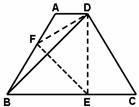
18.如下图,等腰梯形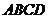 中,
中, ,
,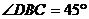 ,翻折梯形
,翻折梯形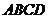 ,使点
,使点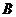 与点
与点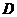 重合,折痕分别交边
重合,折痕分别交边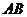 、
、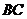 于点
于点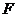 、
、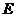 ,若
,若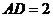 ,
,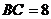 .
.
(1)求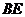 的长;
的长;
(2)求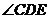 的正切值.
的正切值.
19.已知:如下图,点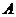 是⊙
是⊙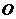 上一点,半径
上一点,半径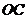 的延长线与过点
的延长线与过点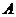 的直线交于点
的直线交于点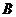 ,
,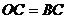 ,
,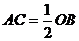 .
.
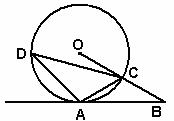
(1)求证: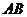 是⊙
是⊙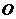 的切线;
的切线;
(2)若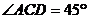 ,
,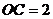 ,求弦
,求弦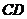 的长.
的长.
五、解答题(本题满分6分)
20.在我国,除夕之夜,全家一起看春节联欢晚会是人们传统的娱乐活动,尤其是小品类节目为我们带来了很多的欢乐。为了统计观众对2009年春晚小品类节目的喜好,中央电视台在网上进行了“2009年春晚我最喜爱的小品”调查问卷,并将统计结果绘制成两幅统计图,请你结合图中所给信息解答下列问题:
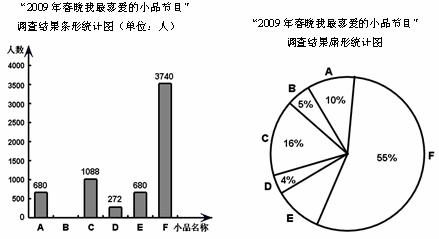
(1)求参加调查的观众喜欢小品《暖冬》的人数占总投票人数的百分比;
(2)求参加调查的观众喜欢小品《黄豆黄》的人数并补全条形图;
(3)若北京市共有1200万人收看了春晚节目,请你估算北京市喜欢小品《不差钱》的观众约有多少人?
(说明:A:《吉祥三宝》;B:《黄豆黄》;C:《水下除夕夜》;D:《北京欢迎你》;E:《暖冬》; F:《不差钱》)
六、解答题(共2个小题,第21题4分,第22题5分,共9分)
21.已知:如下图,直角三角形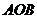 的两直角边
的两直角边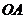 、
、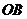 分别在
分别在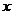 轴的正半轴和
轴的正半轴和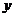 轴的负半轴上,
轴的负半轴上,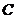 为线段
为线段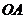 上一点,
上一点,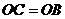 ,抛物线
,抛物线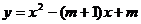 (
(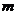 是常数,且
是常数,且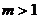 )经过
)经过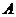 、
、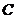 两点.
两点.
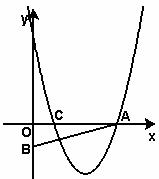
(1)求出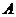 、
、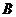 两点的坐标(可用含
两点的坐标(可用含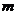 的代数式表示);
的代数式表示);
(2)若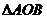 的面积为
的面积为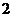 ,求
,求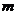 的值.
的值.
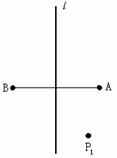
22.在数学小组活动中,小聪同学出了这样一道“对称跳棋”题:如图,在作业本上画一条直线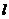 ,在直线
,在直线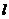 两边各放一粒跳棋子
两边各放一粒跳棋子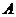 、
、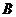 ,使线段
,使线段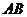 长
长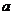 厘米,并关于直线
厘米,并关于直线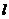 对称,在图中
对称,在图中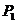 处有一粒跳棋子,
处有一粒跳棋子,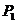 距
距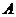 点
点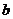 厘米、与直线
厘米、与直线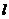 的距离
的距离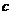 厘米,按以下程序起跳:第
厘米,按以下程序起跳:第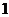 次,从
次,从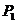 点以
点以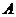 为对称中心跳至
为对称中心跳至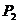 点;第
点;第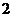 次,从
次,从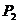 点以
点以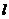 为对称轴跳至
为对称轴跳至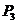 点;第
点;第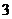 次,从
次,从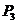 点以
点以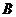 为对称中心跳至
为对称中心跳至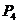 点;第
点;第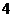 次,从
次,从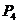 点以
点以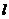 为对称轴跳至
为对称轴跳至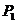 点.
点.
(1)画出跳棋子这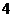 次跳过的路径并标注出各点字母(画图工具不限);
次跳过的路径并标注出各点字母(画图工具不限);
(2)棋子按上述程序跳跃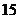 次后停下,假设
次后停下,假设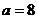 ,
,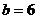 ,
, ,计算这时它与点
,计算这时它与点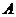 的距离.
的距离.
七、解答题(本题满分7分)
23.两个反比例函数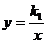 和
和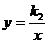 (
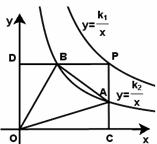
( )在第一象限内的图象如图所示,动点
)在第一象限内的图象如图所示,动点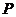 在
在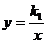 的图象上,
的图象上,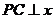 轴于点
轴于点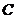 ,交
,交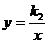 的图象于点
的图象于点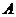 ,
,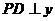 轴于点
轴于点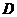 ,交
,交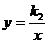 的图象于点
的图象于点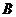 .
.
(1)求证:四边形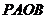 的面积是定值;
的面积是定值;
(2)当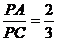 时,求
时,求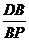 的值;
的值;
(3)若点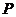 的坐标为(
的坐标为(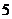 ,
,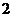 ),
),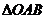 、
、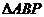 的面积分别记为
的面积分别记为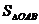 、
、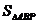 ,设
,设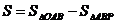 .
.
①求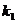 的值;
的值;
②当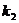 为何值时,
为何值时,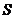 有最大值,最大值为多少?
有最大值,最大值为多少?
八、解答题(本题满分7分)
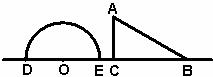
24.已知:如下图,半圆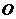 的直径
的直径 ,在
,在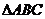 中,
中,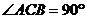 ,
, ,
,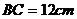 .半圆
.半圆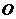 以每秒
以每秒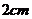 的速度从左向右运动,在运动过程中,点
的速度从左向右运动,在运动过程中,点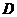 、
、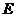 始终在直线
始终在直线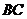 上.设运动时间为
上.设运动时间为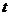 (秒),当
(秒),当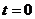 (秒)时,半圆
(秒)时,半圆 在
在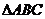 的左侧,
的左侧, .
.
(1)当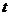 为何值时,
为何值时,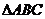 的一边所在直线与半圆
的一边所在直线与半圆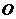 所在的圆相切?
所在的圆相切?
(2)当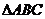 的一边所在直线与半圆
的一边所在直线与半圆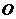 所在的圆相切时,如果半圆
所在的圆相切时,如果半圆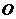 与直线
与直线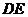 围成的区域与
围成的区域与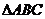 三边围成的区域有重叠部分,求重叠部分的面积.
三边围成的区域有重叠部分,求重叠部分的面积.
九、解答题(本题满分8分)
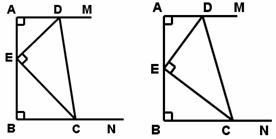
25.已知:如图(1),射线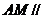 射线
射线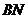 ,
,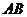 是它们的公垂线,点
是它们的公垂线,点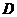 、
、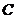 分别在
分别在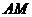 、
、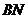 上运动(点
上运动(点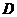 与点
与点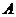 不重合、点
不重合、点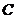 与点
与点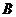 不重合),
不重合),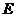 是
是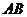 边上的动点(点
边上的动点(点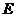 与
与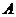 、
、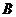 不重合),在运动过程中始终保持
不重合),在运动过程中始终保持 ,且
,且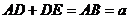 .
.
(1)求证: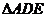 ∽
∽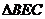 ;
;
(2)如图(2),当点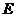 为
为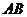 边的中点时,求证:
边的中点时,求证: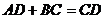 ;
;
(3)设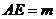 ,请探究:
,请探究: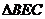 的周长是否与
的周长是否与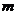 值有关?若有关,请用含有
值有关?若有关,请用含有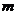 的代数式表示
的代数式表示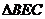 的周长;若无关,请说明理由.
的周长;若无关,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com