
2009年山东省泰安市高中段学校招生考试
数学试卷
注意事项:
1、 本试题分第1卷和第2卷两部分,第1卷3页为选择题,36分;第2卷8页为非选择题,84分;共120分,考试时间120分。
2、 答第1卷前务必将自己的姓名、考号、考试科目涂写在答题卡上,考试结束、试题和答题卡一并收回。
3、 第1卷每题选出答案后,都必须用2B铅笔把答题卡上对应题目的序号标号(ABCD)涂黑如有改动,必须先用橡皮擦干净,在涂改其他答案,不能答在试卷上。
第Ⅰ卷(选择题 共36分)
一、选择题(本大题共12分,在每小题给出的四个选项中,只有一个是正确的,请把正确的答案选出来,每小题选对得3分,选错、不选或选出的答案超过一个,均记0分)
1.下列各式,运算结果为负数的是
A.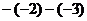 B.
B.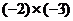 C.
C.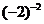 D.
D.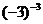
2.光的传播速度约为
A.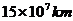 B.
B.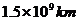 C.
C.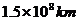 D.
D.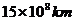
3.抛物线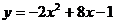 的顶点坐标为
的顶点坐标为
A.(-2,7) B.(-2,-25) C.(2,7) D.(2,-9)
4.如图,⊙O的半径为1,AB是⊙O 的一条弦,且AB=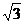 ,则弦AB所对圆周角的度数为
,则弦AB所对圆周角的度数为
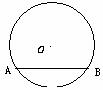
A.30° B.60° C.30°或150° D.60°或120°
5.若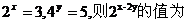
A.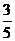 B.
B.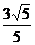 D.
D.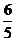
6.如图,是一个工件的三视图,则此工件的全面积是
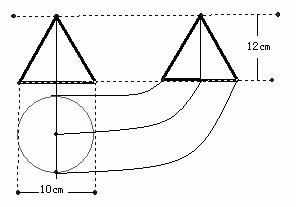
A.85πcm2 B.90πcm
7.如图,△ABC中,D、E分别是BC、AC的中点,BF平分∠ABC,交DE于点F,若BC=6,则DF的长是
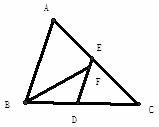
A.2 B.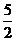 D.4
D.4
8.某服装厂准备加工400套运动装,在加工完160套后,采用了新技术,使得工作效率比原计划提高了20%,结果共用了18天完成任务,问计划每天加工服装多少套?在这个问题中,设计划每天加工x套,则根据题意可得方程为
A.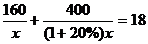 B.
B.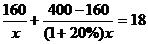
C. 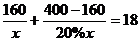 D.
D.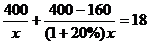
9.在一次夏令营活动中,小亮从位于A点的营地出发,沿北偏东60°方向走了
A.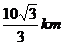 B.
B. C.
C.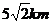 D.
D.
10.某校为了了解七年级学生的身高情况(单位:cm,精确到
分组
一
二
三
四
五
六
七
104-145
145-150
150-155
155-160
160-165
165-170
170-175
人数
6
12
26
4
根据以上信息可知,样本的中位数落在
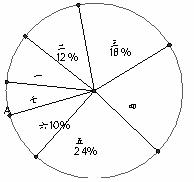
A.第二组 B.第三组 C.第四组 D.第五组
11.如图,在△ABC中,AD是BC边的中线,∠ADC=30°,将△ADC沿AD折叠,使C 点落在C’的位置,若BC=4,则BC’的长为
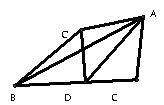
A.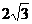 B.
B.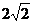 C.4
D.3
C.4
D.3
12.如图,双曲线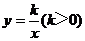 经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为
经过矩形QABC的边BC的中点E,交AB于点D。若梯形ODBC的面积为3,则双曲线的解析式为
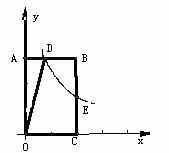
A.
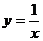 B.
B.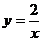 C.
C.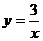 D.
D.
第Ⅱ卷(非选择题 共84分)
注意事项:
1、答卷前将密封线内的项目填写清楚。
2、第Ⅱ卷共8页,用蓝黑钢笔或圆珠笔直接写在试卷上。
二、填空题(本大题7小题,满分21分,只要求填写最后结果,每小题对得3分)
13.化简: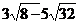 的结果为
。
的结果为
。
14.关于x的一元二次方程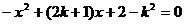 有实数根,则k的取值范围是
。
有实数根,则k的取值范围是
。
x
-1
2
5
y
5
-1
m
15.已知y是x的一次函数,又表给出了部分对应值,则m的值是 。
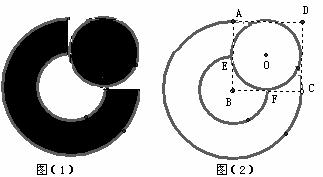
16.如图,(1)是某公司的图标,它是由一个扇环形和圆组成,其设计方法如图(2)所示,ABCD是正方形,⊙O是该正方形的内切圆,E为切点,以B为圆心,分别以BA、BE为半径画扇形,得到如图所示的扇环形,图(1)中的圆与扇环的面积比为 。
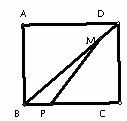
17.如图所示,矩形ABCD中,AB=8,BC=6,P是线段BC上一点(P不与B重合),M是DB上一点,且BP=DM,设BP=x,△MBP的面积为y,则y与x之间的函数关系式为 。
18.如图,在Rt△ABC中,∠ACB=90°,∠A<∠B,沿△ABC的中线CM将△CMA折叠,使点A落在点D处,若CD恰好与MB垂直,则tanA的值为 。

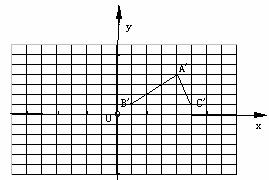
19.如图所示,△A’B’C’是由△ABC向右平移5个单位,然后绕B点逆时针旋转90°得到的(其中A’、B’、C’的对应点分别是A、B、C),点A’的坐标是(4,4)点B’的坐标是(1,1),则点A的坐标是 。
三、解答题(本大题7小题,满分63分,解答应写出必要的文字说明、证明过程或推演步骤)
20.(本小题7分)
先化简、再求值: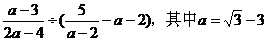 。
。
21.(本小题满分7分)
如图,(1),A、B两个转盘分别被分成三个、四个相同的扇形,分别转动A盘、B盘各一次(若指针恰好指在分割线上,则重转一次,直到指针指向一个数字为止)。
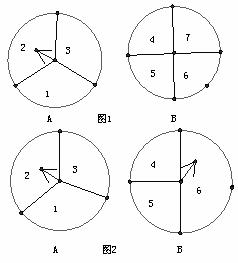
(1)用列表(或画树状图)的方法,求两个指针所指的区域内的数字之和大于7的概率。
(2)如果将图(1)中的转盘改为图(2),其余不变,求两个指针所知区域的数字之和大于7 的概率。
22.(本小题满分9分)
将一个量角器和一个含30度角的直角三角板如图(1)放置,图(2)是由他抽象出的几何图形,其中点B在半圆O的直径DE的延长线上,AB切半圆O于点F,且BC=OD。
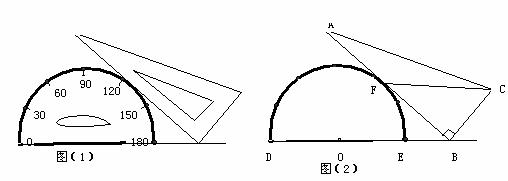
(1)求证:DB∥CF。
(2)当OD=2时,若以O、B、F为顶点的三角形与△ABC相似,求OB。
23.(本小题满分10分)
某旅游商品经销店欲购进A、B两种纪念品,若用380元购进A种纪念品7件,B种纪念品8件;也可以用380元购进A种纪念品10件,B种纪念品6件。
(1) 求A、B两种纪念品的进价分别为多少?
(2) 若该商店每销售1件A种纪念品可获利5元,每销售1件B种纪念品可获利7元,该商店准备用不超过900元购进A、B两种纪念品40件,且这两种纪念品全部售出后总获利不低于216元,问应该怎样进货,才能使总获利最大,最大为多少?
24.(本小题满分10分)
如图,△ABC是直角三角形,∠ACB=90°,CD⊥AB于D,E是AC的中点,ED的延长线与CB的延长线交于点F。
(1)求证:FD2=FB?FC。
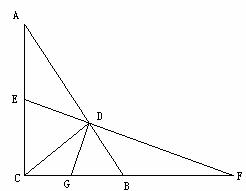
(2)若G是BC的中点,连接GD,GD与EF垂直吗?并说明理由。
25.(本小题满分10分)
如图,△OAB是边长为2的等边三角形,过点A的直线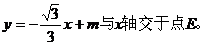

(1)求点E的坐标;
(2)求过 A、O、E三点的抛物线解析式;
(3)若点P是(2)中求出的抛物线AE段上一动点(不与A、E重合),设四边形OAPE的面积为S,求S的最大值。
26.(本小题满分10分)
如图所示,在直角梯形ABCD中,∠ABC=90°,AD∥BC,AB=BC,E是AB的中点,CE⊥BD。
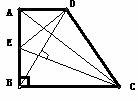
(1)求证:BE=AD;
(2)求证:AC是线段ED的垂直平分线;
(3)△DBC是等腰三角形吗?并说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com