
2009年广东省茂名市初中毕业生学业考试
数学试卷
第Ⅰ卷(选择题,共2页,满分40分)
一、精心选一选(本大题共10个小题,每小题4分,共40分.每小题给出四个答案,其中只有一个是正确的).
1.下列四个数中,其中最小的数是( )
A.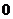 B.
B.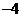 C.
C.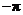 D.
D.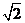
2.下列运算正确的是( )
A.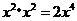 B.
B.
C.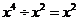 D.
D.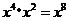
3.如图所示的四个立体图形中,左视图是圆的个数是( )
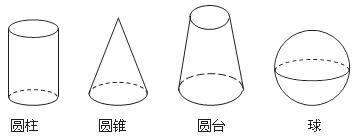
A.4 B.
4.已知一组数据2,2,3, ,5,5,6的众数是2,则
,5,5,6的众数是2,则 是( )
是( )
A.5 B.
5.已知一个多边形的内角和是540°,则这个多边形是( )
A.四边形 B.五边形 C.六边形 D.七边形
6.杨伯家小院子的四棵小树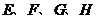 刚好在其梯形院子
刚好在其梯形院子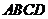 各边的中点上,若在四边形
各边的中点上,若在四边形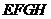 种上小草,则这块草地的形状是(
)
种上小草,则这块草地的形状是(
)
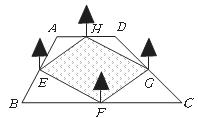
A.平行四边形 B.矩形 C.正方形 D.菱形
7.设从茂名到北京所需的时间是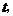 平均速度为
平均速度为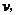 则下面刻画
则下面刻画 与
与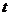 的函数关系的图象是(
)
的函数关系的图象是(
)
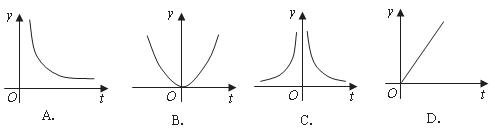
8.分析下列命题:
①四边形的地砖能镶嵌(密铺)地面;
②不同时刻的太阳光照射同一物体,则其影长都是相等的;
③若在正方形纸片四个角剪去的小正方形边长越大,则所制作的无盖长方体形盒子的容积越大.
其中真命题的个数是( )
A.3 B.
9.如图,一把遮阳伞撑开时母线的长是

A.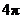 平方米 B.
平方米 B.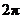 平方米 C.
平方米 C.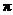 平方米 D.
平方米 D.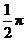 平方米
平方米
10.如图,把抛物线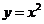 与直线
与直线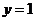 围成的图形
围成的图形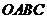 绕原点
绕原点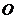 顺时针旋转
顺时针旋转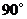 后,再沿
后,再沿 轴向右平移1个单位得到图形
轴向右平移1个单位得到图形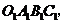 则下列结论错误的是(
)
则下列结论错误的是(
)
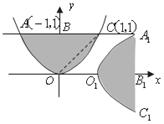
A.点 的坐标是
的坐标是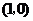 B.点
B.点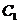 的坐标是
的坐标是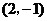
C.四边形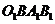 是矩形 D.若连接
是矩形 D.若连接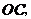 则梯形
则梯形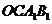 的面积是3
的面积是3
第Ⅱ卷(非选择题,共8页,满分110分)
二、细心填一填(本大题共5小题,每小题4分,共20分.请你把答案填在横线的上方).
11.方程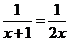 的解是
的解是 .
.
12.如图,在两个同心圆中,三条直径把大圆分成六等份,若在这个圆面上均匀地撒一把豆子,则豆子落在阴影部分的概率是 .
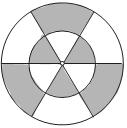
13.若实数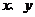 满足
满足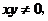 则
则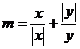 的最大值是
.
的最大值是
.
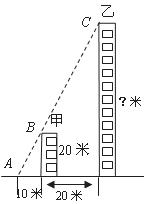
14.如图,甲、乙两楼相距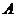 处目测得点
处目测得点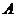 与甲、乙楼顶
与甲、乙楼顶 刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
刚好在同一直线上,若小明的身高忽略不计,则乙楼的高度是 米.
15.我们常用的数是十进制数,而计算机程序处理数据使用的只有数码0和1的二进制数,这二者可以相互换算,如将二进制数1011换算成十进制数应为:
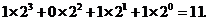 按此方式,则将十进制数6换算成二进制数应为 .
按此方式,则将十进制数6换算成二进制数应为 .
三、用心做一做(本大题共3个小题,每小题8分,共24分).
16.化简或解方程组.
(1)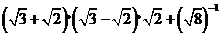 (4分)
(4分)
(2)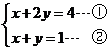 (4分)
(4分)
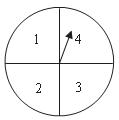
17.如图,把一个转盘分成四等份,依次标上数字1、2、3、4,若连续自由转动转盘二次,指针指向的数字分别记作 把
把 作为点
作为点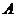 的横、纵坐标.
的横、纵坐标.
(1)求点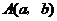 的个数;
(4分)
的个数;
(4分)
(2)求点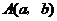 在函数
在函数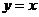 的图象上的概率.(4分)
的图象上的概率.(4分)
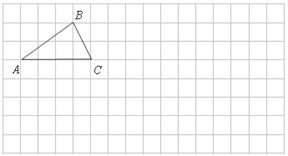
18.如图,方格中有一个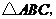 请你在方格内,画出满足条件
请你在方格内,画出满足条件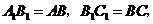
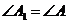 的
的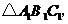 并判断
并判断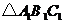 与
与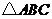 是否一定全等?
是否一定全等?
四、沉着冷静,缜密思考(本大题共2个小题,每小题8分,共16分).
19.某校在“书香满校园”的读书活动期间,学生会组织了一次捐书活动.如图(1)是学生捐图书给图书馆的条形图,图(2)是该学校学生人数的比例分布图,已知该校学生共有1000人.
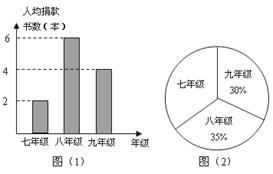
(1)求该校学生捐图书的总本数; (6分)
(2)问该校学生平均每人捐图书多少本? (2分)
20.设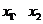 是关于
是关于 的方程
的方程 的两个实数根.试问:是否存在实数
的两个实数根.试问:是否存在实数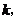 使得
使得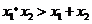 成立,请说明理由.
成立,请说明理由.
五、满怀信心,再接再厉(本大题共3小题,每小题10分,共30分).
21.(本题满分10分)
茂名石化乙烯厂某车间生产甲、乙两种塑料的相关信息如下表,请你解答下列问题:
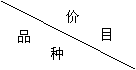
出厂价
成本价
排污处理费
甲种塑料
2100(元/吨)
800(元/吨)
200(元/吨)
乙种塑料
2400(元/吨)
1100(元/吨)
100(元/吨)
每月还需支付设备管理、
维护费20000元
(1)设该车间每月生产甲、乙两种塑料各 吨,利润分别为
吨,利润分别为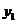 元和
元和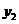 元,分别求
元,分别求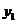 和
和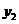 与
与 的函数关系式(注:利润=总收入-总支出);(6分)
的函数关系式(注:利润=总收入-总支出);(6分)
(2)已知该车间每月生产甲、乙两种塑料均不超过400吨,若某月要生产甲、乙两种塑料共700吨,求该月生产甲、乙塑料各多少吨,获得的总利润最大?最大利润是多少?(4分)
22.(本题满分10分)
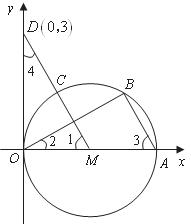
已知:如图,直径为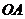 的
的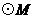 与
与 轴交于点
轴交于点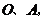 点
点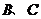 把
把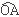 分为三等份,连接
分为三等份,连接 并延长交
并延长交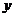 轴于点
轴于点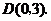
(1)求证: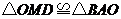 ; (6分)
; (6分)
(2)若直线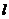 :
: 把
把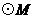 的面积分为二等份,求证:
的面积分为二等份,求证: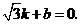 (4分)
(4分)
23.(本题满分10分)
据茂名市某移动公司统计,该公司2006年底手机用户的数量为50万部,2008年底手机用户的数量达72万部.请你解答下列问题:
(1)求2006年底至2008年底手机用户数量的年平均增长率; (5分)
(2)由于该公司扩大业务,要求到2010年底手机用户的数量不少于103.98万部,据调查,估计从2008年底起,手机用户每年减少的数量是上年底总数量的5%,那么该公司每年新增手机用户的数量至少要多少万部?(假定每年新增手机用户的数量相同). (5分)
六、灵动智慧,超越自我(本大题共2小题,每小题10分,共20分).
24.(本题满分10分)
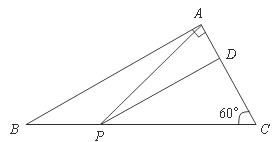
如图,在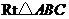 中,
中, 点
点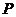 是
是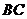 边上的动点(点
边上的动点(点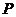 与点
与点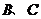 不重合),过动点
不重合),过动点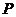 作
作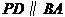 交
交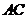 于点
于点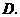
(1)若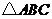 与
与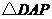 相似,则
相似,则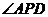 是多少度? (2分)
是多少度? (2分)
(2)试问:当 等于多少时,
等于多少时,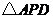 的面积最大?最大面积是多少? (4分)
的面积最大?最大面积是多少? (4分)
(3)若以线段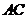 为直径的圆和以线段
为直径的圆和以线段 为直径的圆相外切,求线段
为直径的圆相外切,求线段 的长.(4分)
的长.(4分)
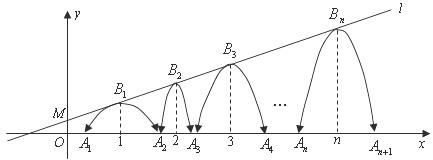
25.(本题满分10分)
已知:如图,直线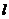 :
: 经过点
经过点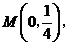 一组抛物线的顶点
一组抛物线的顶点
 (
(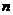 为正整数)依次是直线
为正整数)依次是直线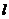 上的点,这组抛物线与
上的点,这组抛物线与 轴正半轴的交点依次是:
轴正半轴的交点依次是:
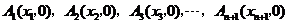 (
(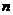 为正整数),设
为正整数),设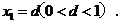
(1)求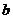 的值; (2分)
的值; (2分)
(2)求经过点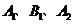 的抛物线的解析式(用含
的抛物线的解析式(用含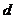 的代数式表示) (4分)
的代数式表示) (4分)
(3)定义:若抛物线的顶点与 轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
轴的两个交点构成的三角形是直角三角形,则这种抛物线就称为:“美丽抛物线”.
探究:当 的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的
的大小变化时,这组抛物线中是否存在美丽抛物线?若存在,请你求出相应的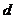 的值. (4分)
的值. (4分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com