
2009-2010学年度烟台招远第一学期九年级第二学段测评
数学试题
时间:120分钟 满分:150分
一、选择题:(将唯一正确答案代号填在括号内每小题3分,满分45分)
1.当你乘车沿一条平坦的大道向前行驶时,你会发现,前方那些较高的建筑物好像“沉”到了位于它们与车之间的那些较矮的建筑物后面去了。这是因为
A.汽车开得很快  B.盲区减小
B.盲区减小
C.盲区增大 D.以上都不对
2.若⊙O的直径为10,圆心O为坐标原点,点P的坐标为(4,3),则点P与⊙O的位置关系是
A.点P在⊙O上 B.点P在⊙O内
C.点P在⊙O外 D.以上都有可能
3.下列等式:①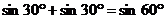 ;②
;②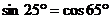 ;③
;③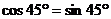 ;
;
④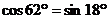 .其中正确的个数是
.其中正确的个数是
A.1个 B.2个 C.3个 D.4个
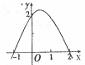
4.二次函数的图象如下图所示,则其表达式是
A.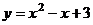 B.
B.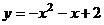
C.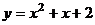 D.
D.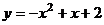
5.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是

6.P是⊙O外一点,PA、PB分别与⊙O相切于点A、B,点C是劣弧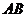 上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则
上任意一点,经过点C作⊙O的切线,分别交PA、PB于点D、E.若PA=4,则 的周长是
的周长是
A.4 B.8 C.12 D.不能确定
7.在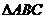 中,
中, ,
,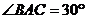 ,AD是中线,则
,AD是中线,则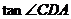 的值为
的值为
A.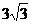 B.
B.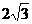 C.
C.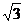 D.
D.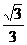
8.下列左图是一个水管的三叉接头,其左视图是
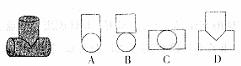
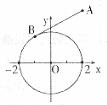
9.如图,⊙O的半径为2,以O为原点,建立直角坐标系,点A的坐标为(2,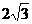 ),直线AB为⊙O的切线,B为切点,则B点的坐标为
),直线AB为⊙O的切线,B为切点,则B点的坐标为
A.(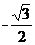 ,
,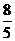 )
B(
)
B(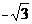 ,1)
,1)
C.(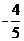 ,
,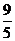 )
D.(一1,
)
D.(一1,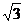 )
)
10.已知两圆的半径比为2:3,当它们内切时,圆心距等于2,则当它们外切时,圆心距等于
A.16  B.14 C.12 D.10
B.14 C.12 D.10
11.如图,晚上小明在路灯下散步,在小明由A处走到B处这一过程中,他在地上的影子的长度
A.逐渐变短 B.逐渐变长
C.先变短后变长 D.先变长后变短

12.如图,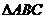 内接于⊙O,⊙O的半径为l,BC=
内接于⊙O,⊙O的半径为l,BC=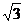 ,则
,则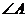 的度数为
的度数为
A.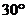 B.
B.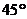 C.
C.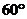 D.
D.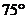
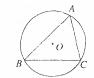
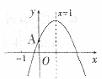
13.如图,开口向下的抛物线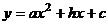 交
交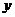 轴的正半轴于点A,对称轴是直线X=1,则下列结论正确的是
轴的正半轴于点A,对称轴是直线X=1,则下列结论正确的是
A.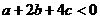 B.
B.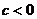
C.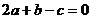 D.
D.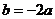
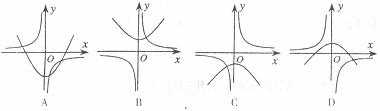
14.二次函数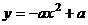 与反比例函数
与反比例函数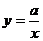 的图象大致是
的图象大致是
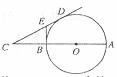
15.如图,AB是⊙O的直径,AB=6,点C是AB延长线上一点,CD是⊙O的切线,点D是切点,过点B作⊙O的切线,交CD于点E若CD=4,则点E到⊙O的切线长ED等于
A.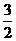 B.
B.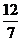 C.
C.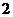 D.
D.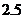
二、填空题:(将正确答案填在横线上.每小题4分,满分40分)
16.在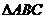 中,若
中,若 ,AB=13,AC=5,则
,AB=13,AC=5,则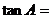 __________.
__________.
17.小华在距离路灯
18.抛物线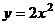 不动,把
不动,把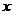 轴、
轴、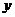 轴分别向上、向左平移3个单位,则在新坐标系下,此抛物线的解析式为__________(可不化成一般形式).
轴分别向上、向左平移3个单位,则在新坐标系下,此抛物线的解析式为__________(可不化成一般形式).
19.如图,在半径为
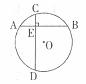
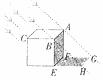
20.如图,正方体的棱长为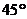 角,则图中阴影部分(四边形EFGH)的面积为__________平方米.
角,则图中阴影部分(四边形EFGH)的面积为__________平方米.
21.如图,已知△ABC内接于⊙O,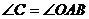 ,OA=
,OA=
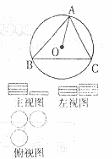
22.一张桌子上重叠摆放了若干枚面值1元的硬币,它的三种视图如下图所示,则桌子上共有1元硬币_______枚。
23.请选择一组你喜欢的a、b、c的值,写出一个二次函数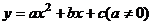 ,使其同时满足下列条件:①图象开口向下;②当
,使其同时满足下列条件:①图象开口向下;②当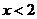 时,
时,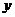 随
随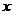 的增大而增大;当
的增大而增大;当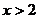 时,
时,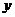 随
随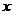 的增大而减小。你所写的二次函数的表达式是______________
的增大而减小。你所写的二次函数的表达式是______________
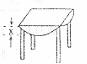
24.如图,用一块直径为a的圆桌布平铺在对角线长为a的正方形桌面上,若四周下垂的最大长度x相等,则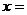 _______。
_______。
25.如图,扇形AOB的半径为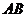 于点A,且交OB的延长线于点C,如果
于点A,且交OB的延长线于点C,如果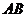 长
长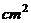
三、解答题:(每小题10分,满分30分)
26.如图,△ABC中, ,BC=3,AC=4,D为AC上一点,以CD为直径的⊙O切AB于点E.求⊙O的半径长.
,BC=3,AC=4,D为AC上一点,以CD为直径的⊙O切AB于点E.求⊙O的半径长.
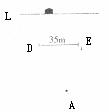
27.如图,小明家(点A处)和公路(L)之间竖立着一块
(1)请在图中画出视点A的盲区,并将盲区的那段公路记为BC;
(2)若一辆以
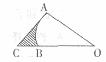
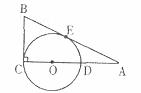
28.如图, 是直角三角形,
是直角三角形,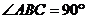 ,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE
,以AB为直径的⊙O交AC于点E,点D是BC边的中点,连接DE
(1)求证:DE是⊙O的切线;
(2)若⊙O的半径为4,DE=3,求AE的长。
四、实际应用题:(每小题10分,满分20分)
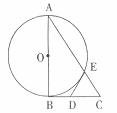
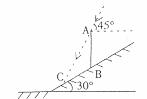
29.如图,在一个坡角为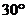 的斜坡上有一电线杆AB,当太阳光与水平线成
的斜坡上有一电线杆AB,当太阳光与水平线成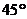 角时,测得该杆在斜坡上的影长BC为
角时,测得该杆在斜坡上的影长BC为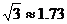 ,
,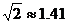 ).
).
30.某商店以每件20元的价格购进一批商品,如果以每件30元销售,那么半月内可售出400件。根据销售经验,销售单价每提高1元,半月内的销售量相应减少20件如何提高销售单价,才能在半月内获得最大利润?最大利润是多少?
五、探索题:(满分15分)
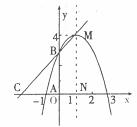
31.如图,抛物线的顶点坐标为M(1,4),与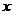 轴的一个交点是A(一1,0),与
轴的一个交点是A(一1,0),与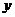 轴交于点B,直线
轴交于点B,直线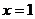 交
交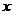 轴于点N。
轴于点N。
(1)求抛物线的解析式及点B的坐标;
(2)求经过B、M两点的直线的解析式,并求出此直线与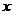 轴的交点C的坐标;
轴的交点C的坐标;
(3)若点P在抛物线的对称轴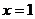 上运动,请你探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过点A,并且与直线BM相切若存在,求出点P的坐标;若不存在,请说明理由。
上运动,请你探索:在x轴上方是否存在这样的P点,使以P为圆心的圆经过点A,并且与直线BM相切若存在,求出点P的坐标;若不存在,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com