
上海市2009年高考模拟试题汇编
函数
一、填空题
1、(2009上海卢湾区4月模考)(2009上海卢湾区4月模考)设 的反函数为
的反函数为 ,若函数
,若函数 的图像过点
的图像过点 ,且
,且 , 则
, 则 .
.
2、(2009上海十四校联考)已知 上的函数,且
上的函数,且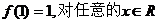 都有下列两式成立:
都有下列两式成立:
 的值为
的值为
1
3、(2009上海八校联考)某同学在研究函数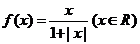 时,分别给出下面几个结论:
时,分别给出下面几个结论:
①等式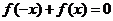 对
对 恒成立;
恒成立;
②函数 的值域为
的值域为 ;
;
③若 ,则一定有
,则一定有 ;
;
④函数 在
在 上有三个零点。
上有三个零点。
其中正确结论的序号有________________。(请将你认为正确的结论的序号都填上)
①②③
3、(2009冠龙高级中学3月月考)已知函数 ,若
,若 ,则实数
,则实数 的取值范围是 。
的取值范围是 。

4、(2009闵行三中模拟)若函数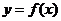 的值域是
的值域是 ,则函数
,则函数 的值域是 。
的值域是 。

5、(2009上海普陀区)已知函数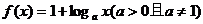 ,
, 是
是 的反函数,若
的反函数,若 的图像过点
的图像过点 ,则
,则 .
.
2
6、(2009上海十校联考)已知函数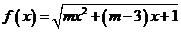 的值域是
的值域是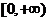 ,则实数
,则实数 的取值范围是________________.
的取值范围是________________.

7、(2009上海闸北区)函数 的定义域为___________.
的定义域为___________.
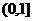
8、(2009重点九校联考)函数 的定义域为 .
的定义域为 .
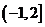
二、解答题
1、(2009上海八校联考)对定义在 上,并且同时满足以下两个条件的函数
上,并且同时满足以下两个条件的函数 称为
称为 函数。
函数。
① 对任意的 ,总有
,总有 ;
;
② 当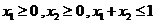 时,总有
时,总有 成立。
成立。
已知函数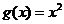 与
与 是定义在
是定义在 上的函数。
上的函数。
(1)试问函数 是否为
是否为 函数?并说明理由;
函数?并说明理由;
(2)若函数 是
是 函数,求实数
函数,求实数 组成的集合;
组成的集合;
解:(1)当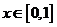 时,总有
时,总有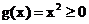 ,满足①,…………1分
,满足①,…………1分
当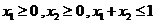 时,
时,
 ,满足②……4分
,满足②……4分
(2)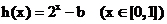 为增函数,
为增函数,

 ………5分
………5分
由 ,得
,得 ,
,
即 …………6分
…………6分
因为 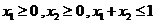
所以 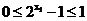
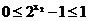
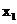 与
与 不同时等于1
不同时等于1
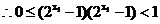 ;
;  …………8分
…………8分
当 时,
时,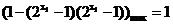 ;
;  …………9分
…………9分
综合上述: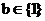 …………10分
…………10分
2、(2009上海十校联考)已知函数 ,
, 有反函数,且函数
有反函数,且函数 的最大值为
的最大值为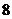 ,求实数
,求实数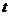 的值.
的值.
【解】 因为函数有反函数,所以在定义域内是一一对应的
函数 的对称轴为
的对称轴为 ,所以
,所以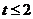 或
或 …… 3分
…… 3分
若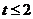 ,在区间
,在区间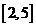 上函数是单调递增的,所以
上函数是单调递增的,所以 ,解得
,解得 ,符合
…… 7分
,符合
…… 7分
若 ,在区间
,在区间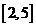 上函数是单调递减的,所以
上函数是单调递减的,所以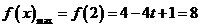 ,解得
,解得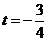 ,与
,与 矛盾,舍去
…… 11分
矛盾,舍去
…… 11分
综上所述,满足题意的实数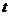 的值为
的值为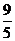 ……12分
……12分
3、(2009上海闸北区)设 ,其中实常数
,其中实常数 .
.
(Ⅰ)求函数 的定义域和值域;
的定义域和值域;
(Ⅱ)试研究函数 的基本性质,并证明你的结论.
的基本性质,并证明你的结论.
[解](Ⅰ)函数 的定义域为
的定义域为 …………………………………………………………2分
…………………………………………………………2分
 ,
,
当 时,因为
时,因为 ,所以
,所以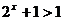 ,
,
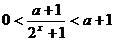 ,从而
,从而 ,…………………………………………..4分
,…………………………………………..4分
所以函数 的值域为
的值域为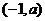 .………………………………………………..1分
.………………………………………………..1分
(Ⅱ)假设函数 是奇函数,则,对于任意的
是奇函数,则,对于任意的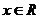 ,有
,有 成立,
成立,
即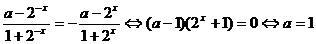
 当
当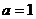 时,函数
时,函数 是奇函数.…………………………………………………….3分
是奇函数.…………………………………………………….3分
当 ,且
,且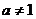 时,函数
时,函数 是非奇非偶函数.……………………………….1分
是非奇非偶函数.……………………………….1分
 对于任意的
对于任意的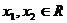 ,且
,且 ,
,


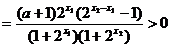 ……………………………………..4分
……………………………………..4分
 当
当 时,函数
时,函数 是递减函数.……………………………………..1分
是递减函数.……………………………………..1分
4、(2009重点九校联考)已知指数函数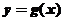 满足:g(2)=4,
满足:g(2)=4,
定义域为 的函数
的函数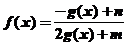 是奇函数。
是奇函数。
(1)确定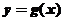 的解析式;
的解析式;
(2)求m,n的值;
(3)若对任意的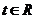 ,不等式
,不等式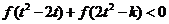 恒成立,求实数
恒成立,求实数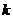 的取值范围。
的取值范围。
解:
解:(1) 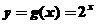 ………4分
………4分
(2)由(1)知: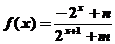
因为 是奇函数,所以
是奇函数,所以 =0,即
=0,即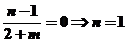 ……………5分
……………5分
∴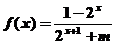 , 又由f(1)= -f(-1)知
, 又由f(1)= -f(-1)知
 ………8分
………8分
(3)由(2)知 ,
,
易知 在
在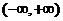 上为减函数。…9分
上为减函数。…9分
又因 是奇函数,从而不等式:
是奇函数,从而不等式:
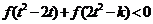 等价于
等价于 ,
,
因 为减函数,由上式推得:
为减函数,由上式推得: …10分
…10分
即对一切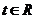 有:
有: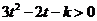 ,
,
从而判别式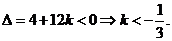 …………………14分
…………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com