
高一年级第二学期周练卷(1)2009.2.19
班级 姓名 学号 成绩
一、选择题:(每小题4分,共32分)
1.设指数函数 ,则下列等式中不正确的是 ( )D
,则下列等式中不正确的是 ( )D
A.f(x+y)=f(x)?f(y) B.
C. D.
D.

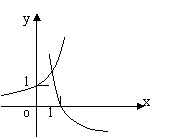

 2.当
2.当 时,在同一坐标系中,函数
时,在同一坐标系中,函数 的图象是
( )C
的图象是
( )C
A B C D
3.下列指数式与对数式互化不正确的一组是 ( )C
A.  B.
B.

C.  D.
D.

4.设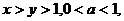 则下列关系正确的是
( )C
则下列关系正确的是
( )C
A. B.
B. C.
C. D.
D.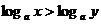
5.函数 的值域是 ( )A
的值域是 ( )A
A. B.
B. C.
C. D.R
D.R
6.设 时,
时,  的取值范围是( )C
的取值范围是( )C
A. B.
B. C.
C. D.以上都不对
D.以上都不对
7.函数 ,满足
,满足 的
的 的取值范围 ( )D
的取值范围 ( )D
A. B.
B. 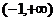
C. D.
D.
8.函数 得单调递增区间是 ( )D
得单调递增区间是 ( )D
A. B.
B. C.
C. D.
D.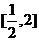
二、填空题:(每小题4分,共44分)
9.函数 与函数
与函数 的图像关于 Y轴
对称
的图像关于 Y轴
对称
10. 等于
14
等于
14
11.设 ,若
,若 ,则
,则
 。
。
12.函数y= ,xÎ(0,1)的值域是
(-1,0)
,xÎ(0,1)的值域是
(-1,0)
13.已知函数f (x)的定义域是(1,2),则函数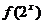 的定义域是
. (0,1);
的定义域是
. (0,1);
14.当a>0且a≠1时,函数 必过定点
. (2,-2);
必过定点
. (2,-2);
15.计算 =
.
=
.
 ;
;
16.已知-1<a<0,则三个数 由小到大的顺序是
.
由小到大的顺序是
.

17. ,则
,则 与
与 的大小关系是
。<
的大小关系是
。<
18.函数 的反函数是
。f -1(x)=log5(x+1),x>-1
的反函数是
。f -1(x)=log5(x+1),x>-1
19.已知 有意义,则
有意义,则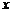 的取值范围是
。
的取值范围是
。
(答: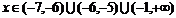 )
)
三、解答题:解答应写出文字说明、证明过程或演算步骤(共24分).
20.(10分)已知 ,试用p,q表示lg5.
,试用p,q表示lg5.
解:  , lg5=
, lg5=

21.(14分)已知
(1)求 的定义域;
的定义域;
(2)证明 为奇函数;
为奇函数;
(3)求使 >0成立的x的取值范围. (14分)
>0成立的x的取值范围. (14分)
解:(1)

(2)证明:

 中为奇函数.
中为奇函数.
(3)解:当a>1时,  >0,则
>0,则 ,则
,则

因此当a>1时,使 的x的取值范围为(0,1).
的x的取值范围为(0,1).
 时,
时, 
则
解得
因此 时, 使
时, 使 的x的取值范围为(-1,0).
的x的取值范围为(-1,0).
高一年级第二学期周练卷(1)答案2009.2.19
一、选择题:(每小题4分,共32分)
1.设指数函数 ,则下列等式中不正确的是 ( )D
,则下列等式中不正确的是 ( )D
A.f(x+y)=f(x)?f(y) B.
C. D.
D.



 2.当
2.当 时,在同一坐标系中,函数
时,在同一坐标系中,函数 的图象是
( )C
的图象是
( )C
A B C D
3.下列指数式与对数式互化不正确的一组是 ( )C
A.  B.
B.

C.  D.
D.

4.设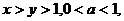 则下列关系正确的是
( )C
则下列关系正确的是
( )C
A. B.
B. C.
C. D.
D.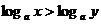
5.函数 的值域是 ( )A
的值域是 ( )A
A. B.
B. C.
C. D.R
D.R
6.设 时,
时,  的取值范围是( )C
的取值范围是( )C
A. B.
B. C.
C. D.以上都不对
D.以上都不对
7.函数 ,满足
,满足 的
的 的取值范围 ( )D
的取值范围 ( )D
A. B.
B. 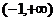
C. D.
D.
8.函数 得单调递增区间是 ( )D
得单调递增区间是 ( )D
A. B.
B. C.
C. D.
D.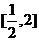
二、填空题:(每小题4分,共44分)
9.函数 与函数
与函数 的图像关于 Y轴
对称
的图像关于 Y轴
对称
10. 等于 14
等于 14
11.设 ,若
,若 ,则
,则
 。
。
12.已知函数f (x)的定义域是(1,2),则函数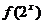 的定义域是
. (0,1);
的定义域是
. (0,1);
13.当a>0且a≠1时,函数 必过定点 . (2,-2);
必过定点 . (2,-2);
14.函数y= ,xÎ(0,1)的值域是
(-1,0)
,xÎ(0,1)的值域是
(-1,0)
15.若点(1,7)既在函数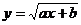 的图像上,又在其反函数的图像上,则数对
的图像上,又在其反函数的图像上,则数对 为
。(-8,57)
为
。(-8,57)
16.已知-1<a<0,则三个数 由小到大的顺序是
.
由小到大的顺序是
.

17.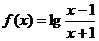 ,
, ,则
,则 与
与 的大小关系是
。<
的大小关系是
。<
18.函数 的反函数是
。f -1(x)=log5(x+1),x>-1
的反函数是
。f -1(x)=log5(x+1),x>-1
19.已知 有意义,则
有意义,则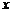 的取值范围是
。
的取值范围是
。
(答: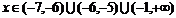 )
)
三、解答题:解答应写出文字说明、证明过程或演算步骤(共24分).
20.(10分)已知 ,试用 p,q 表示lg5.
,试用 p,q 表示lg5.
解:  , lg5=
, lg5=

21.(14分)已知
(1)求 的定义域;
的定义域;
(2)证明 为奇函数;
为奇函数;
(3)求使 成立的x的取值范围.
成立的x的取值范围.
解:(1)

(2)证明:

 中为奇函数.
中为奇函数.
(3)解:当a>1时,  >0,则
>0,则 ,则
,则

因此当a>1时,使 的x的取值范围为(0,1).
的x的取值范围为(0,1).
 时,
时, 
则
解得
因此 时, 使
时, 使 的x的取值范围为(-1,0).
的x的取值范围为(-1,0).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com