
湖北省武汉市武昌区 2009届高三年级五月调研测试
理 科 数 学 试 卷
2009.5.21
本试卷满分150分,考试用时120分钟.
注意事项:
1.答卷前,考生务必将自已的姓名、准考证号填写在试题卷和答题卡上,并将准
考证号条形码粘贴在答题卡上的指定位置。
2.选择题选出答案后,有2B铅笔把答题卡上对应题目的答案标号涂黑。如需改
动,用橡皮擦干净后,再选涂其他答案标号。非选择题用黑色墨水的签字笔直接答在
答题卡上。答在试题卷上无效。
参考公式:
如果事件A、B互斥,那么
如果事件A、B相互独立,那么
如果事件A在一次试验中发生的概率是 ,那么n次独立重复试验中恰好发生k次的概率
,那么n次独立重复试验中恰好发生k次的概率
球的表面积公式 ,其中
,其中 表示球的半径
表示球的半径
球的体积公式 ,其中
,其中 表示球的半径
表示球的半径
一.选择题:本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知I为实数集,集合 ,则
,则 =( )
=( )
A. B.
B. C.
C. D.
D.
2.复数 的共轭复数的平方为( )
的共轭复数的平方为( )
A.1+2 i B.3+2
i B.3+2 i C.-1-2
i C.-1-2 i D.-1+2
i D.-1+2 i
i
3.函数f(x)在点x=x0处有定义是f(x)在点x=x0处有极限的( )
A.充分条件,但不是必要条件 B.必要条件,但不是充分条件
C.充要条件 D.既非充分也非必要的条件
4.已知直线 按向量
按向量 平移后得到的直线
平移后得到的直线 与圆
与圆 相切,那么
相切,那么 的值为( )
的值为( )
A. 或1 B.0或
或1 B.0或 C.
C. 或7 D.
或7 D. 或
或
 5.如图,P为△OAB所在平面上一点,
5.如图,P为△OAB所在平面上一点, , 且P在线段AB的垂直平分线上,向量
, 且P在线段AB的垂直平分线上,向量 ,若
,若  ,则
,则 =( )
=( )
A.  B.
B.  D.
D.

6.已知等比数列 的公比为
的公比为 ,其前
,其前 项和为
项和为 ,若
,若 成等差数列,则
成等差数列,则 等于( )
等于( )
A. B.
B. 或1
D.
或1
D. 或
或
7.设f(x)为可导函数,且满足 ,则过曲线y=f(x)上一点
,则过曲线y=f(x)上一点 处的切线斜率为( )
处的切线斜率为( )
A.4 B D.
D.
8.设a,b,m为正整数,若a和b除以m的余数相同,则称a和b对m同余. 记作 ,已知
,已知 ,则b的值可以是( )
,则b的值可以是( )
A. 1012 B.
 9.如图,已知球
9.如图,已知球 是棱长为2 的正方体
是棱长为2 的正方体  的内切球,则平面
的内切球,则平面 截球
截球 的截
的截
面面积为 ( )
A. B.
B.
C. D.
D. 
10.已知点P是椭圆 上的动点,F
上的动点,F 、F
、F 分别为椭圆的左、右焦点,O为坐标原点,则
分别为椭圆的左、右焦点,O为坐标原点,则 的取值范围( )
的取值范围( )
A.[0, ] B. [0,
] B. [0, ] C. [0,2 ) D.
] C. [0,2 ) D. 
二.填空题:本大题共5小题,每小题5分,共25分.把答案填在答题卡相应位置上.
11.双曲线 的焦点坐标为
.
的焦点坐标为
.
12.已知角 满足条件
满足条件 ,则
,则 的值为
.
的值为
.
13若 表示的平面区域是三角形,则实数
表示的平面区域是三角形,则实数 的取值范围是
.
的取值范围是
.
14.某次抽样调查结果表明,考生的成绩(百分制)近似服从正态分布,平均成绩为72分,96分以上的考生占考生总数的2.3%,则考生成绩在60至84分之间的概率为 . (参考数据: =0.8413,
=0.8413, =0.9770,
=0.9770, =0.9987)
=0.9987)
15.设函数 使关于
使关于 的不等式
的不等式 在
在 至少存在一个解,则实数
至少存在一个解,则实数 的取值范围为
的取值范围为
三.解答题:本大题共6小题,共75分,解答应写出文字说明,证明过程或演算步骤.
16.(本小题满分12分)
已知 ,
, ,其中
,其中 ,设函数
,设函数 .
.
(1)求函数 的单调增区间;
的单调增区间;
(2)若关于 的方程
的方程 有两相异实根,求实数
有两相异实根,求实数 的取值范围.
的取值范围.
17.(本小题满分12分)
为了迎接中华人民共和国建国60周年,中央电视台为庆典拟举办一期选拔节目,选拔一批素质较为过硬的群众参加天安门城楼的义务服务工作,假定符合参加选拔条件的每个选手还需要进行四轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考核,否则即被淘汰.已知某选手能正确回答第一、二、三、四轮问题的概率分别为 ,
, ,
, ,
, ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(2)该选手在选拔过程中回答过的问题的总个数记为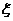 ,求随机变量
,求随机变量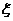 的分布列与数学期望.
的分布列与数学期望.
18.(本小题满分12分)
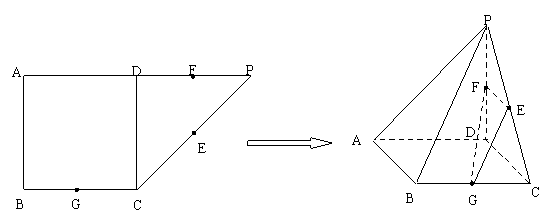
如图所示,在直角梯形ABCP中,AP//BC,AP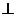 AB, AB=BC=
AB, AB=BC=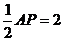 ,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将
,D是AP的中点,E,F,G分别为PC、PD、CB的中点,将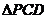 沿CD折起,使得
沿CD折起,使得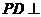 平面ABCD.
平面ABCD.
(1)求证:AP//平面EFG;
 (2) 求
(2) 求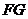 与平面
与平面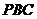 所成角的大小.
所成角的大小.
(3)求二面角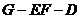 的大小.
的大小.
19.(本小题满分12分)
已知点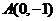 ,点
,点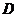 在
在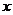 轴上,点
轴上,点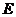 在
在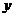 轴正半轴上,点
轴正半轴上,点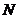 满足
满足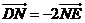 ,
,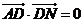 .
.
(1)求动点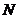 的轨迹
的轨迹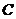 的方程;
的方程;
(2)已知点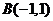 ,若过点
,若过点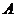 的动直线
的动直线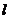 交轨迹
交轨迹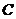 于
于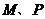 两点,直线
两点,直线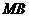 交轨迹
交轨迹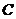 于另一点
于另一点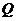 ,证明直线
,证明直线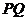 恒过一个定点,并求出定点坐标.
恒过一个定点,并求出定点坐标.
20.(本小题满分13分)
已知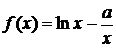 .
.
(1)当a>0时,判断f(x)在定义域上的单调性;
(2)若f(x)在[1,e]上的最小值为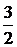 ,求a的值;
,求a的值;
(3)若f(x)<x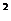 在(1,+
在(1,+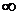 )上恒成立,试求a的取值范围.
)上恒成立,试求a的取值范围.
21.(本小题满分14分)
把正奇数列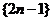 中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设
中的数按上小下大,左小右大的原则排列成如图“三角形”所示的数表.设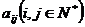 是位于这个三角形数表中从上往下数第
是位于这个三角形数表中从上往下数第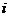 行,从左向右数第
行,从左向右数第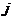 个数.
个数.
(1)若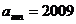 ,求
,求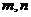 的值;
的值;
(2)已知函数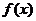 的反函数为
的反函数为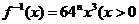 ,
,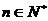 ),若记三角形数表中从上往下数第
),若记三角形数表中从上往下数第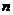 行各数的和为
行各数的和为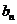 .①求数列
.①求数列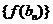 的前
的前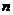 项的和
项的和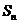 .②令
.②令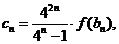
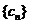 的前
的前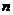 项之积为
项之积为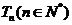 ,求证:
,求证: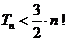
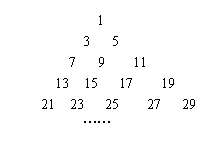
且当 或
或 时,
时, .当
.当 时,
时, . …………………………10分
. …………………………10分
结合图象可知所求 的取值范围为
的取值范围为 . ……………………………………12分
. ……………………………………12分
17.解:(1)记“该选手能正确回答第 轮问题”的事件为
轮问题”的事件为 ,
,
则 .
.
该选手进入第四轮才被淘汰的概率:

 .……………6分
.……………6分
(2)由题意 的所有可能取值分别是1, 2, 3, 4,且
的所有可能取值分别是1, 2, 3, 4,且
 ,
,
 ,
,

方法二: 连AC,BD交于O点,连GO,FO,EO.
∵E,F分别为PC,PD的中点,
∴ //
// ,同理
,同理 //
//
又 //AB,
//AB, //
//
 平面EFG//平面PAB.
平面EFG//平面PAB.
又PA 平面PAB,
平面PAB, 平面EFG.………………………………………4分
平面EFG.………………………………………4分
(2)由已知底面ABCD是正方形, 
 .
.
又∵ 面ABCD,
面ABCD, .
.
又 ,
, 平面PCD,
平面PCD, .
.
过点F作 于
于 ,则
,则 .
.
连结 ,则
,则 为直线
为直线 与平面
与平面 所成的角. …………………6分
所成的角. …………………6分
由 ∽
∽ ,得
,得 .在
.在 中求得
中求得 .
.

而 ,
, ,
,
 .
.

 .即动点
.即动点 的轨迹
的轨迹 的方程为
的方程为 .…………4分
.…………4分
(2)设点 ,
, ,
, .
.
 三点共线,
三点共线, ,即
,即 .
.
即 ,
, . ………………………………………6分
. ………………………………………6分
 三点共线,
三点共线, ,即
,即 .
.
 ,即
,即 .
.

 =f(e)=1-
=f(e)=1- =
= ,得a=
,得a= (舍去). …………………………………6分
(舍去). …………………………………6分
③若 即-e<a<-1,则
即-e<a<-1,则 在(1,
在(1, )上为减函数,在(
)上为减函数,在( ,e)上为增函时数.
,e)上为增函时数. =f(-a)=
=f(-a)= =
= ,得
,得 .
.
综上知a=- .……………………………………………………………………8分
.……………………………………………………………………8分
(3)由 ,得
,得 .
.
令 ,则
,则 .
.
于是 .由
.由 知
知 .
.
 在
在 上单调递减,从而
上单调递减,从而 .
.
所以 在
在 上单调递减,于是
上单调递减,于是

∴ . ………………………………………………………8分
. ………………………………………………………8分
② ,
,

即证: . …………………………………10分
. …………………………………10分
先证: .
.
1° 时,显然成立.
时,显然成立.
2°假设 时,
时, .
.
则 时,
时,


 ,即当
,即当 时,也成立.
时,也成立.
由1°2°知 成立.
成立.
从而
 . ………………………………………14分
. ………………………………………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com