
2009届安徽高考信息交流试卷
数学(理科)试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷为第1至第2页,第Ⅱ卷为第3垒第4页.全卷满分150分,考试时问120分钟.
考生注意事项:
1.答题前,考生务必在试题卷、答题卡规定的地方填写自己的座位号、姓名.考生要认真核对答题卡上粘贴的条形码的“考场座位号、姓名”与考生本人考场座位号、姓名是否一致.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后.再选出其他答案标号.第Ⅱ卷用0.5毫米的黑色签字笔在答题卡上书写作答,在试题卷上作答,答案无效.
3.考试结束,监考员将试题卷和答题卡一井收回.
参考公式:
如果事件(A、B}互斥,那么 球的表面积公式
P(A+B)=P(A)+P(B)

如果事件(A、B}相互独立,那么 其中R表示球的半径
P(A?B)=P(A)?P(B) 球的体积公式
如果事件A在一次试验中发生的概率是P,那么 
n次独立重复实验中恰好发生k次的概率 其中R表示球的半径

第Ⅰ卷 (选择题 共55分)
一、选择题:本大题共11题,每小题5分,共55分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知函数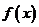 =
=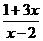 (x≠2),则其反函数
(x≠2),则其反函数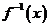 的一个单调递减区间是
的一个单调递减区间是
A.(-∞,十∞) B.(-3,+∞)
C.(3,+∞) D.以上都不对
2.已知p:不等式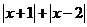 >
>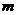 的解集为R;q:
的解集为R;q: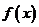 =
=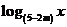 为减函数,则p成立是q成立的
为减函数,则p成立是q成立的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
3.对于任意直线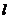 与平面
与平面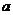 ,在平面
,在平面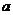 内必有直线
内必有直线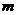 与
与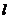
A.平行 B.相交 C.垂直 D.互为异面直线
4.已知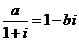 ,其中
,其中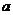 、b是实数.
、b是实数.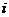 是虚数单位,则
是虚数单位,则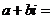
A.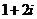 B.
B.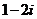 C.
C.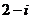 D.2
D.2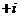
5.设全集U=R,集合M=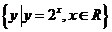 ,N=
,N=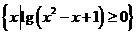 ,则下列关系式中正确的是
,则下列关系式中正确的是
A.M∩N∈M B.M∪N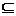 M
M
C.M∪N=R D.(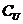 M)∩N=
M)∩N=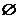
6.已知函数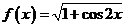 =,则
=,则
A.函数图像关于直线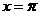 对称 B.函数图像关于点(
对称 B.函数图像关于点(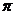 ,0)对称
,0)对称
 C.函数在区间
C.函数在区间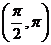 上递减 D.函数在区间
上递减 D.函数在区间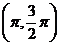 上递增
上递增
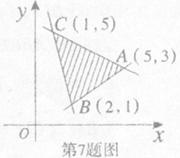
7.给出平面区域(图中阴影部分)作为可行域.其中A(5,3),B(2,1),C(1,5)。若目标函数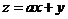 (
(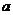 >0)取得最大值的最优解有无穷多个.则
>0)取得最大值的最优解有无穷多个.则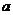 的值为
的值为
A.4 B.2
C.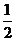 D.
D.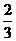
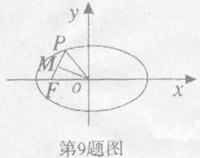
8.已知三棱锥S―ABC的四个顶点在以O为球心的同一球面上,且SA=SB=SC=AB,∠ACB=90。,则当球的表面积为400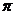 时。点O到平面ABC的距离为
时。点O到平面ABC的距离为
A.4 B.
 9.设P是椭圆
9.设P是椭圆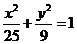 上的一点,F是椭圆的左焦点,且
上的一点,F是椭圆的左焦点,且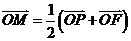 ,
,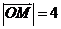 ,则点P到该椭圆左准线的距离为
,则点P到该椭圆左准线的距离为
A.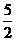 B.3
B.3
C.4 D.6
10.若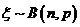 ,且
,且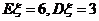 ,则P(
,则P(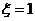 |)的值为
|)的值为
A.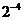 B.
B.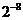 C.
C.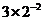 D.
D.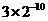
l1.若函数y=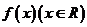 满足
满足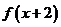 =
=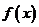 ,且
,且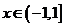 时,
时,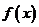 =
=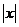 ,则函数
,则函数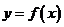 的图像与函数
的图像与函数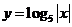 的图像交点个数是
的图像交点个数是
A.2 B.
第Ⅱ卷 (非选择题 共95分)
(用0.
二、填空题:本大题共4小题,每小题4分,共16分.把答案填在答题卡的相应位置.
12.设 ,则
,则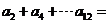 _________________.
_________________.
13.已知向量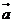 =(1,1),
=(1,1),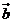 =(1,-1),
=(1,-1),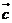 =(
=(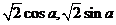 )(
)(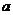 ∈R),实数
∈R),实数 满足
满足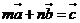 ,则
,则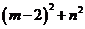 的最大值为_____________.
的最大值为_____________.
14.一个无穷等比数列的公比为q,满足0<q<l,前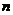 项和为
项和为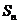 ,且它的第4项与第8项之和等与
,且它的第4项与第8项之和等与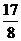 ,第5项与第7项之积等与
,第5项与第7项之积等与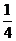 ,则
,则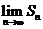 =_________________。
=_________________。
15.如图,正方体ABCD―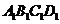 的棱长为1,M是
的棱长为1,M是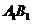 的中点,则下列四个命题:
的中点,则下列四个命题:
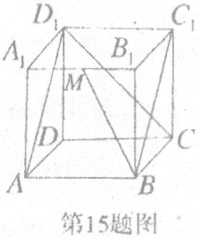 ①直线
①直线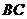 与平面
与平面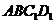 所成的角等于45°;
所成的角等于45°;
②四面体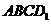 在正方体六个面内的摄影图形面积的最小值为
在正方体六个面内的摄影图形面积的最小值为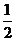 ;
;
③点M到平面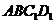 的距离是
的距离是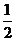 ;
;
④BM与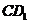 所成的角为
所成的角为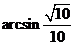 ,其中真命题的序号是____________________。
,其中真命题的序号是____________________。
三、解答题:本大题共6小题,共79分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分12分)
在周长为6的△ABC中,∠A、∠B 、∠C所对的边分别为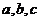 ,若
,若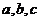 成等比数列;
成等比数列;
(1)求B的取值范围;
(2)求△ABC的面积S的最大值;
(3) 当△ABC的面积S最大时,过△ABC的重心G作直线交边AB于M,交边AC与N,设∠AGM=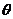 ,
,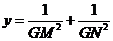 试证:
试证: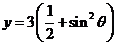 。
。
17.(本小题满分14分)
如图,在四棱锥P-ABCD中,PB⊥底面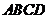 ,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
,CD⊥PD,底面ABCD为直角梯形,AD∥BC,AB⊥BC,AB=AD=PB=3,点E在棱PA上,且PE=2EA。
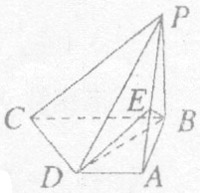 (1)求异面直线PA与CD所成的角;
(1)求异面直线PA与CD所成的角;
(2)求证:PC∥平面EBD;
(3)求二面角A-BE-D的大小。
18.(本小题满分12分)
一次智力竞赛中,共分三个环节:选答、抢答、风险选答,在第一环节“选答”中.每个选手可以从6道题(其中4道选择题,2道操作题)中任意选3道题作答,答对每道题可得100分;在第二环节“抢答”中,一共为参赛选手准备了5道抢答题.答对一道得1 00分,在每一道题的抢答中,每位选手抢到的概率是相等的;在第三环节“风险选答”中,一共为选手准备了A、B、C 三类不同的题目,选手每答对一道A类、B类、C类的题目将分别得到300分、200分、100分,但如果答错,则相应地要扣除300分、200分、100分.而选手答对一道A类、B类、C类题目的概率分别是0.6、0.7、0.8,现有甲、乙、丙三位选手参加比赛,试求:
(1)乙选手在第一环节中,至少选中一道操作题的概率;
(2)甲选手在第二环节中抢到的题数多于乙选手而不多于丙选手的概率;
(3)在第三环节中,就每道题而言,丙选手选择哪类题目得分的期望值更大.
19.(本小题满分I 3分)
某容器中装有浓度为r%的溶液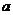 ml,倒出
ml,倒出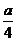 ml后,再倒入浓度为p%的溶液
ml后,再倒入浓度为p%的溶液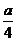 ml(P>r)搅匀,如此反复操作,设第n次操作后溶液的浓度为
ml(P>r)搅匀,如此反复操作,设第n次操作后溶液的浓度为 %,第n+1次操作后溶液的浓度为
%,第n+1次操作后溶液的浓度为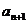 %.
%.
(1)求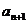 与
与 的关系式;
的关系式;
(2)求第n次操作后溶液的浓度 %;
%;
(3)记: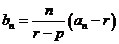 。求数列
。求数列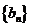 的前n项和
的前n项和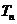 。
。
20.(本小题满分14分)
已知函数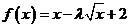 在
在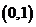 上单调递减,
上单调递减,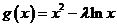 在
在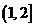 上单调递增.
上单调递增.
(1)求实数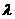 的值;
的值;
(2)求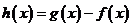 的最小值;
的最小值;
(3)当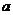 >1时,若
>1时,若 ≥
≥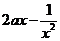 在
在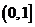 上恒成立,求
上恒成立,求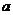 的取值范围.
的取值范围.
21.(本小题满分I 4分)
已知两定点A(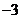 ,0),B(3,0),动圆M与直线AB相切于点N.且
,0),B(3,0),动圆M与直线AB相切于点N.且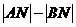 =4,现分别过点A、B作动圆M的切线(异于直线AB),两切线相交于点P.
=4,现分别过点A、B作动圆M的切线(异于直线AB),两切线相交于点P.
(1)求动点P的轨迹方程;
(2)若直线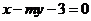 截动点P的轨迹所得的弦长为5,求m的值;
截动点P的轨迹所得的弦长为5,求m的值;
(3)设过轨迹上的点P的直线与两直线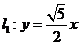 ,
,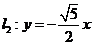 分别交于点
分别交于点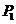 ,
,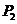 ,且点
,且点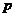 分有向线段
分有向线段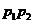 所成的比为
所成的比为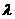 (
(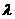 >0),当
>0),当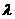 ∈
∈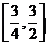 时,求
时,求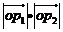 的最小值与最大值。
的最小值与最大值。
2009届安徽高考信息交流试卷
一、选择题
题号
1
2
3
4
5
6
7
8
9
10
11
答案
C
B
C
D
C
A
C
B
A
D
C
提示与分析:
1. ,故选C。
,故选C。
2.易知p成立,m<3,q成立,2<m< ,从而p成立
,从而p成立 成立,故选B。
成立,故选B。
3.选C
4.由已知得 即
即 ,得
,得 ,故选D。
,故选D。
5.易知 ,故选C。
,故选C。
6. ,作图知选A。
,作图知选A。
7.选C。由题: 。
。
8.设球半径为R,由 ,由
,由 知,三棱锥顶点S爱底面ABC内的摄影D是△ABC的外心,又∠ACB=90°,∴D是AB的中点,点O到ABC的距离h=OD,设SA=SB=SC=AB=2
知,三棱锥顶点S爱底面ABC内的摄影D是△ABC的外心,又∠ACB=90°,∴D是AB的中点,点O到ABC的距离h=OD,设SA=SB=SC=AB=2 ,可得
,可得
 ,或h=10(舍),故选B。
,或h=10(舍),故选B。
9.由题设易知M是PF的中点,设椭圆右焦点为 ,由
,由 知,
知, =8,
=8, ,又易知该椭圆的离心率
,又易知该椭圆的离心率 ,再由椭圆第二定义得,点P到椭圆左准线的距离
,再由椭圆第二定义得,点P到椭圆左准线的距离 ,故选A。
,故选A。
10.由 ,∴
,∴ 故选D。
故选D。
11.由题设知 是周期为2的周期函数,由
是周期为2的周期函数,由 时,
时, ,可作出
,可作出 再R上的简图,又
再R上的简图,又 是偶函数,再作出简图,则可确定两图像的交点个数,故选C。
是偶函数,再作出简图,则可确定两图像的交点个数,故选C。
二、填空题
12.112 13.9 14.32 15.①②④
提示与分析:
12.令 得
得 ,再分别令
,再分别令 得两式,再相加可得
得两式,再相加可得 ,从而得知
,从而得知 。
。
13.由题得: ,
, 得:
得: ,而
,而 可看作是单位圆上的点(m,n)到点(2,0)的距离,则易知,
可看作是单位圆上的点(m,n)到点(2,0)的距离,则易知, 的最大值为9.
的最大值为9.
14.由题设知, 又0<q<1则得
又0<q<1则得 ,∴
,∴
15.如图,①知直线BC与面 所成的角即为∠
所成的角即为∠ ,故①正确。
,故①正确。
②易知四面体 在四个侧面的摄影图形面积均最小,为正方形面积之半,故②正确
在四个侧面的摄影图形面积均最小,为正方形面积之半,故②正确
③点M到平面 的距离,即为点
的距离,即为点 到平面
到平面 的距离。其等于
的距离。其等于 ,故③不正确。
,故③不正确。
④易知BM与 所成的角,即为BM与
所成的角,即为BM与 所成的角,设∠
所成的角,设∠ ∠
∠ 易知
易知 ,
, ,即
,即 ,故④正确。
,故④正确。
三、解答题
16.(1)由题设知:
再由余弦定理得:
当且仅当 时取等号,故所求B的取值范围是
时取等号,故所求B的取值范围是 (3分)
(3分)
(2)∵ ,∴
,∴ ,
,
∴0<b ,当且仅当
,当且仅当 时,
时,
∴
∴ (6分)
(6分)
(3)由(1)(2)易知,当△ABC的面积S最大时,△ABC是边长为2的正△,此时易知 ∠
∠ ∠
∠
 在△AGM中,由正弦定理得:
在△AGM中,由正弦定理得:
则
在△AGN中,同理可得:
 (10分)
(10分)
∴ (或用降次公式化简)
(或用降次公式化简)


 (12分)
(12分)
17.解法一:
(1)由PB⊥面ABCD,CD⊥PD知CD⊥BD
 在直角梯形ABCD中,AD⊥AB,AB=AD=3,
在直角梯形ABCD中,AD⊥AB,AB=AD=3,
∴BD= ,BC=6
,BC=6
取BC的中点F,连结AF,则AF∥CD,
∴PA与CD所成的角就是∠PAF (4分)
连PF由题设易知AF=PF=PA= ,
,
∴∠PAF=60°即为所求 (6分)
(2)连AC交BD于G,连EG,易知 ,
,
又 ∴
∴ ,∴PC∥EG,又EG
,∴PC∥EG,又EG 面EBD,∴PC∥面EBD (10分)
面EBD,∴PC∥面EBD (10分)
(3)∵PB⊥面ABCD,∴AD⊥PB,
又AD⊥AB,∴AD⊥面EAB
作AH⊥BE于H,连DH,则DH⊥BE, (12分)
在△AEB中,易求得BE= ,
,
在 △DAH中,
△DAH中, ∠
∠
即所求二面角的大小为 (14分)
(14分)
 解法二:(1)如图建立空间直角坐标系
解法二:(1)如图建立空间直角坐标系 ,设
,设

则A(0,3,0),P(0,0,3)D(3,3,0),C( ,0,0),
,0,0), =
=
∵ ,∴
,∴ ,
,
即:3(3- )+9=0
)+9=0 (2分)
(2分)
∴
∴
∴ ,即异面直线PA与CD所成的交为60°
(6分)
,即异面直线PA与CD所成的交为60°
(6分)
(2)设平面BED的法向量为 ∵
∵
由 得
得
 ,∴
,∴ (12分)
(12分)
又由(1)知 ,∴
,∴ ,∴PC∥面EBD (10分)
,∴PC∥面EBD (10分)
(3)由(2)知
又平面ABE的法向量 ,
,
故所求二面角的大小为 (14分)
(14分)
18.(1)在第一环节中,乙选手从6道题目中任选3道至少有1道操作题的概率
 (4分)
(4分)
(2)在第二环节中,甲抢到的题目多于乙选手而不多于丙选手的情况有以下三种:
甲、乙、丙三位选手抢到的题目的个数分别为1,0,4;2,0,3;2,1,2,
故所求的概率


(8分)
(3)在第三个环节中,就每一次答题而言,丙选手得分是一个随机变量 ,
,
若选A类题,其得分的期望是 (分)
(分)
若选B类题,其得分的期望是 (分)
(分)
若选C类题,其得分的期望是 (分)
(分)
由于 >
> =
= ,故丙应选B类得分的切望值更大。(12分)
,故丙应选B类得分的切望值更大。(12分)
19.(1)依题意可得:
(4分)
(2)由

当 时,
时, ,则
,则
∴ ,∴
,∴
即第 次操作后溶液的浓度为
次操作后溶液的浓度为 (9分)
(9分)
(3)由(2)可得:
则
由错位相减法可求得:

故所求 (13分)
(13分)
20.(1)由 <0,
<0, >
> ,∴
,∴
又 >
> <
< ,∴
,∴
从而有  (4分)
(4分)
(2)由(1)可知,
故 ,则
,则
令 >
> ∵
∵ >
> 得
得 >
> ,∴
,∴ >
>
令 <
< ∵
∵ >
> ,解得
,解得 <
< <
<
列表:

(0,1)
1
(1,+∞)

-
0
+

↓
0
↑
即  在
在 处有最小值0 (8分)
处有最小值0 (8分)
(3)由 易知
易知 时,
时, <
<
∴ 为减函数,其最小值为1
为减函数,其最小值为1
令 在
在 上单增,其最大值为
上单增,其最大值为
依题意得:
又 >
> ∴
∴ <
< (14分)
(14分)
21.(1)由题设及平面几何知识得: <
< ,
,
∵动点P的轨迹是以A、B为交点的双曲线右支,
由
故所求P点的轨迹方程为: (4分)
(4分)
(2)易知 直线 恒过双曲线焦点B(3,0)
恒过双曲线焦点B(3,0)
设该直线与双曲线右支相交于
由双曲线第二定义知,
又 ∴
∴ ,则
,则 ,
,
由 得
得 ,从而易知,仅当
,从而易知,仅当 时,
时, 满足
满足
故所求 (8分)
(8分)
(3)设 ,且p分有向线段
,且p分有向线段 所成的比为
所成的比为 ,
,
则 ,
, ,
,
又点 在双曲线
在双曲线 上,∴
上,∴
化简得:
又

∴ (11分)
(11分)
令
∵ 在
在 上单减,在
上单减,在 上单增,
上单增,
又 ,∴
,∴ 在
在 上单减,在
上单减,在 上单增,∴
上单增,∴
又
 ,∴
,∴
故所求 的最小值为9,最大值为
的最小值为9,最大值为 。 (14分)
。 (14分)
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
天星教育网(www.tesoon.com) 版权所有
| ||||||||||||||||||||||||||||||||||