
二轮复习中坐标系与参数方程的必会题
前言:坐标系与参数方程的题目市面上及其罕见,本套测试题来源于广东,而且大部分都是原创题,是一套不可多得的优秀复习材料。
[基础训练A组]
一、选择题
1.若直线的参数方程为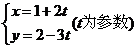 ,则直线的斜率为( )
,则直线的斜率为( )
A.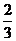 B.
B.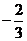
C.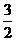 D.
D.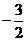
2.下列在曲线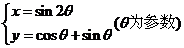 上的点是( )
上的点是( )
A.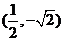 B.
B.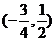 C.
C.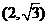 D.
D.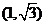
3.将参数方程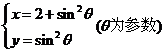 化为普通方程为( )
化为普通方程为( )
A.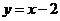 B.
B.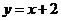 C.
C. D.
D.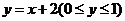
4.化极坐标方程 为直角坐标方程为( )
为直角坐标方程为( )
A. B.
B.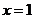 C.
C.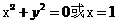 D.
D.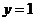
5.点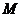 的直角坐标是
的直角坐标是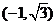 ,则点
,则点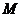 的极坐标为( )
的极坐标为( )
A.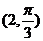 B.
B.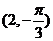 C.
C.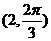 D.
D.
6.极坐标方程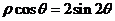 表示的曲线为( )
表示的曲线为( )
A.一条射线和一个圆 B.两条直线 C.一条直线和一个圆 D.一个圆
二、填空题
1.直线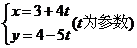 的斜率为______________________。
的斜率为______________________。
2.参数方程 的普通方程为__________________。
的普通方程为__________________。
3.已知直线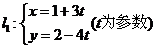 与直线
与直线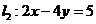 相交于点
相交于点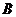 ,又点
,又点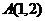 ,
,
则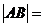 _______________。
_______________。
4.直线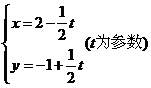 被圆
被圆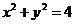 截得的弦长为______________。
截得的弦长为______________。
5.直线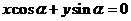 的极坐标方程为____________________。
的极坐标方程为____________________。
三、解答题
1.已知点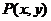 是圆
是圆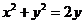 上的动点,
上的动点,
(1)求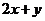 的取值范围;
的取值范围;
(2)若 恒成立,求实数
恒成立,求实数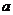 的取值范围。
的取值范围。
2.求直线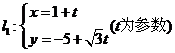 和直线
和直线 的交点
的交点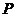 的坐标,及点
的坐标,及点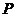
与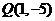 的距离。
的距离。
3.在椭圆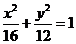 上找一点,使这一点到直线
上找一点,使这一点到直线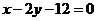 的距离的最小值。
的距离的最小值。
[综合训练B组]
一、选择题
1.直线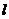 的参数方程为
的参数方程为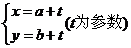 ,
,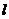 上的点
上的点 对应的参数是
对应的参数是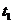 ,则点
,则点 与
与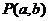 之间的距离是( )
之间的距离是( )
A.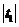 B.
B.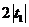 C.
C.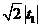 D.
D.
2.参数方程为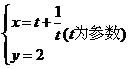 表示的曲线是( )
表示的曲线是( )
A.一条直线 B.两条直线 C.一条射线 D.两条射线
3.直线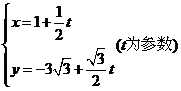 和圆
和圆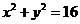 交于
交于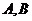 两点,
两点,
则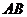 的中点坐标为( )
的中点坐标为( )
A.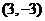 B.
B.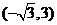 C.
C.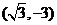 D.
D.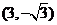
4.圆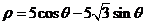 的圆心坐标是( )
的圆心坐标是( )
A.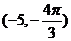 B.
B.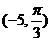 C.
C.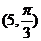 D.
D.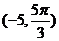
5.与参数方程为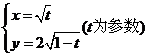 等价的普通方程为( )
等价的普通方程为( )
A. B.
B.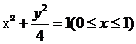
C.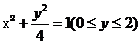 D.
D.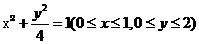
6.直线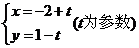 被圆
被圆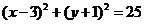 所截得的弦长为( )
所截得的弦长为( )
A.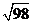 B.
B.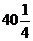 C.
C.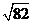 D.
D.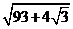
二、填空题
1.曲线的参数方程是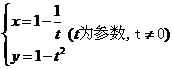 ,则它的普通方程为__________________。
,则它的普通方程为__________________。
2.直线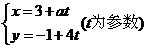 过定点_____________。
过定点_____________。
3.点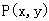 是椭圆
是椭圆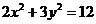 上的一个动点,则
上的一个动点,则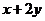 的最大值为___________。
的最大值为___________。
4.曲线的极坐标方程为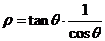 ,则曲线的直角坐标方程为________________。
,则曲线的直角坐标方程为________________。
5.设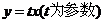 则圆
则圆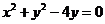 的参数方程为__________________________。
的参数方程为__________________________。
三、解答题
1.参数方程 表示什么曲线?
表示什么曲线?
2.点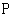 在椭圆
在椭圆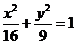 上,求点
上,求点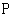 到直线
到直线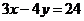 的最大距离和最小距离。
的最大距离和最小距离。
3.已知直线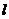 经过点
经过点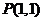 ,倾斜角
,倾斜角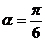 ,
,
(1)写出直线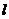 的参数方程。
的参数方程。
(2)设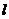 与圆
与圆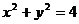 相交与两点
相交与两点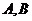 ,求点
,求点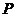 到
到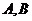 两点的距离之积。
两点的距离之积。
[提高训练C组]
一、选择题
1.把方程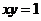 化为以
化为以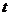 参数的参数方程是( )
参数的参数方程是( )
A.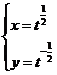 B.
B. C.
C.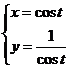 D.
D.
2.曲线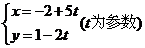 与坐标轴的交点是( )
与坐标轴的交点是( )
A.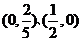 B.
B.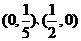
C.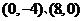 D.
D.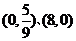
3.直线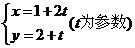 被圆
被圆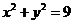 截得的弦长为( )
截得的弦长为( )
A. B.
B.
C.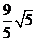 D.
D.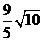
4.若点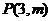 在以点
在以点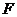 为焦点的抛物线
为焦点的抛物线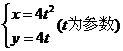 上,
上,
则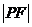 等于( )
等于( )
A.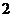 B.
B.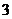
C. D.
D.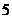
5.极坐标方程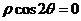 表示的曲线为( )
表示的曲线为( )
A.极点 B.极轴
C.一条直线 D.两条相交直线
6.在极坐标系中与圆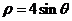 相切的一条直线的方程为( )
相切的一条直线的方程为( )
A.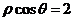 B.
B.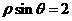
C. D.
D.
二、填空题
1.已知曲线 上的两点
上的两点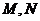 对应的参数分别为
对应的参数分别为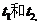 ,
,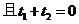 ,那么
,那么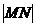 =_______________。
=_______________。
2.直线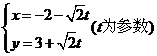 上与点
上与点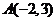 的距离等于
的距离等于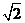 的点的坐标是_______。
的点的坐标是_______。
3.圆的参数方程为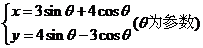 ,则此圆的半径为_______________。
,则此圆的半径为_______________。
4.极坐标方程分别为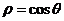 与
与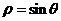 的两个圆的圆心距为_____________。
的两个圆的圆心距为_____________。
5.直线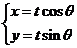 与圆
与圆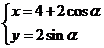 相切,则
相切,则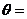 _______________。
_______________。
三、解答题
1.分别在下列两种情况下,把参数方程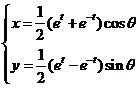 化为普通方程:
化为普通方程:
(1)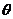 为参数,
为参数,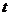 为常数;(2)
为常数;(2)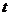 为参数,
为参数,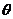 为常数;
为常数;
2.过点 作倾斜角为
作倾斜角为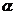 的直线与曲线
的直线与曲线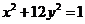 交于点
交于点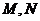 ,
,
求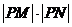 的值及相应的
的值及相应的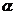 的值。
的值。
坐标系与参数方程 [基础训练A组]
一、选择题
1.D 
2.B 转化为普通方程: ,当
,当 时,
时,
3.C 转化为普通方程: ,但是
,但是
4.C 
5.C  都是极坐标
都是极坐标
6.C 
则 或
或
二、填空题
1.

2.

3. 将
将 代入
代入 得
得 ,则
,则 ,而
,而 ,得
,得
4. 直线为
直线为 ,圆心到直线的距离
,圆心到直线的距离 ,弦长的一半为
,弦长的一半为 ,得弦长为
,得弦长为
5.
 ,取
,取
三、解答题
1.解:(1)设圆的参数方程为 ,
,


(2)

2.解:将 代入
代入 得
得 ,
,
得 ,而
,而 ,得
,得
3.解:设椭圆的参数方程为 ,
,

当 时,
时, ,此时所求点为
,此时所求点为 。
。
坐标系与参数方程 [综合训练B组]
一、选择题
1.C 距离为
2.D  表示一条平行于
表示一条平行于 轴的直线,而
轴的直线,而 ,所以表示两条射线
,所以表示两条射线
3.D  ,得
,得 ,
,
中点为
4.A 圆心为
5.D 
6.C  ,把直线
,把直线 代入
代入
 得
得
 ,弦长为
,弦长为
二、填空题
1.
 而
而 ,
,
即
2.
 ,
, 对于任何
对于任何 都成立,则
都成立,则
3. 椭圆为
椭圆为 ,设
,设 ,
,

4.
 即
即
5.
 ,当
,当 时,
时, ;当
;当 时,
时, ;
;
而 ,即
,即 ,得
,得
三、解答题
1.解:显然 ,则
,则

即
得 ,即
,即
2.解:设 ,则
,则
即 ,
,
当 时,
时, ;
;
当 时,
时, 。
。
3.解:(1)直线的参数方程为 ,即
,即
(2)把直线 代入
代入
得
 ,则点
,则点 到
到 两点的距离之积为
两点的距离之积为
坐标系与参数方程 [提高训练C组]
一、选择题
1.D  ,
, 取非零实数,而A,B,C中的
取非零实数,而A,B,C中的 的范围有各自的限制
的范围有各自的限制
2.B 当 时,
时, ,而
,而 ,即
,即 ,得与
,得与 轴的交点为
轴的交点为 ;
;
当 时,
时, ,而
,而 ,即
,即 ,得与
,得与 轴的交点为
轴的交点为
3.B  ,把直线
,把直线 代入
代入
 得
得
 ,弦长为
,弦长为
4.C 抛物线为 ,准线为
,准线为 ,
, 为
为 到准线
到准线 的距离,即为
的距离,即为
5.D  ,为两条相交直线
,为两条相交直线
6.A  的普通方程为
的普通方程为 ,
, 的普通方程为
的普通方程为
圆 与直线
与直线 显然相切
显然相切
二、填空题
1. 显然线段
显然线段 垂直于抛物线的对称轴。即
垂直于抛物线的对称轴。即 轴,
轴,
2. ,或
,或

3. 由
由 得
得
4. 圆心分别为
圆心分别为 和
和
5. ,或
,或 直线为
直线为 ,圆为
,圆为 ,作出图形,相切时,
,作出图形,相切时,
易知倾斜角为 ,或
,或
三、解答题
1.解:(1)当 时,
时, ,即
,即 ;
;
当 时,
时,
而 ,即
,即
(2)当 时,
时, ,
, ,即
,即 ;
;
当 时,
时, ,
, ,即
,即 ;
;
当 时,得
时,得 ,即
,即
得
即 。
。
2.解:设直线为 ,代入曲线并整理得
,代入曲线并整理得

则
所以当 时,即
时,即 ,
, 的最小值为
的最小值为 ,此时
,此时 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com