
题目列表(包括答案和解析)
| π |
| 3 |
|
| 1 | cosθ |
| π |
| 6 |
| 3 |
| 3 |
(极坐标与参数方程)已知曲线C的极坐标方程是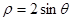 ,直线l的参数方程是
,直线l的参数方程是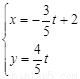 (t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,则MN的最大值为____________
(t为参数).设直线l与x轴的交点是M,N是曲线C上一动点,则MN的最大值为____________
曲线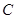 的极坐标方程为
的极坐标方程为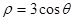 ,则曲线
,则曲线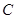 的直角坐标方程为_______________.
的直角坐标方程为_______________.
坐标系与参数方程 [基础训练A组]
一、选择题
1.D 
2.B 转化为普通方程: ,当
,当 时,
时,
3.C 转化为普通方程: ,但是
,但是
4.C 
5.C  都是极坐标
都是极坐标
6.C 
则 或
或
二、填空题
1.

2.

3. 将
将 代入
代入 得
得 ,则
,则 ,而
,而 ,得
,得
4. 直线为
直线为 ,圆心到直线的距离
,圆心到直线的距离 ,弦长的一半为
,弦长的一半为 ,得弦长为
,得弦长为
5.
 ,取
,取
三、解答题
1.解:(1)设圆的参数方程为 ,
,


(2)

2.解:将 代入
代入 得
得 ,
,
得 ,而
,而 ,得
,得
3.解:设椭圆的参数方程为 ,
,

当 时,
时, ,此时所求点为
,此时所求点为 。
。
坐标系与参数方程 [综合训练B组]
一、选择题
1.C 距离为
2.D  表示一条平行于
表示一条平行于 轴的直线,而
轴的直线,而 ,所以表示两条射线
,所以表示两条射线
3.D  ,得
,得 ,
,
中点为
4.A 圆心为
5.D 
6.C  ,把直线
,把直线 代入
代入
 得
得
 ,弦长为
,弦长为
二、填空题
1.
 而
而 ,
,
即
2.
 ,
, 对于任何
对于任何 都成立,则
都成立,则
3. 椭圆为
椭圆为 ,设
,设 ,
,

4.
 即
即
5.
 ,当
,当 时,
时, ;当
;当 时,
时, ;
;
而 ,即
,即 ,得
,得
三、解答题
1.解:显然 ,则
,则

即
得 ,即
,即
2.解:设 ,则
,则
即 ,
,
当 时,
时, ;
;
当 时,
时, 。
。
3.解:(1)直线的参数方程为 ,即
,即
(2)把直线 代入
代入
得
 ,则点
,则点 到
到 两点的距离之积为
两点的距离之积为
坐标系与参数方程 [提高训练C组]
一、选择题
1.D  ,
, 取非零实数,而A,B,C中的
取非零实数,而A,B,C中的 的范围有各自的限制
的范围有各自的限制
2.B 当 时,
时, ,而
,而 ,即
,即 ,得与
,得与 轴的交点为
轴的交点为 ;
;
当 时,
时, ,而
,而 ,即
,即 ,得与
,得与 轴的交点为
轴的交点为
3.B  ,把直线
,把直线 代入
代入
 得
得
 ,弦长为
,弦长为
4.C 抛物线为 ,准线为
,准线为 ,
, 为
为 到准线
到准线 的距离,即为
的距离,即为
5.D  ,为两条相交直线
,为两条相交直线
6.A  的普通方程为
的普通方程为 ,
, 的普通方程为
的普通方程为
圆 与直线
与直线 显然相切
显然相切
二、填空题
1. 显然线段
显然线段 垂直于抛物线的对称轴。即
垂直于抛物线的对称轴。即 轴,
轴,
2. ,或
,或

3. 由
由 得
得
4. 圆心分别为
圆心分别为 和
和
5. ,或
,或 直线为
直线为 ,圆为
,圆为 ,作出图形,相切时,
,作出图形,相切时,
易知倾斜角为 ,或
,或
三、解答题
1.解:(1)当 时,
时, ,即
,即 ;
;
当 时,
时,
而 ,即
,即
(2)当 时,
时, ,
, ,即
,即 ;
;
当 时,
时, ,
, ,即
,即 ;
;
当 时,得
时,得 ,即
,即
得
即 。
。
2.解:设直线为 ,代入曲线并整理得
,代入曲线并整理得

则
所以当 时,即
时,即 ,
, 的最小值为
的最小值为 ,此时
,此时 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com